АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Гидродинамическое подобие
Теория подобия позволяет представить дифференциальные уравнения Навье—Стокса в виде некоторой функции от критериев подобия. Эти критерии будут характеризовать силы, действующие при движении вязкой жидкости.
Напишем уравнение Навье—Стокса относительно только одной вертикальной оси г\
|
Dwg, dw, . dwz. dw. |
|
Р Гд |
|
2 dz |
= Ч + І-Й) (A)
3 dz
И выполним подобное преобразование этого уравнения:
А а2 fdwz at dwz dwz dwz\
PW ■РІ-дГ-Б^ + ^-аГ + ^^Г =
At
|
1 dO |
|
Ц AH + |
|
3 dz |
|
Ai |
|
Аг |
|
Умножив все члены полученного уравнения на |
|
АЛ |
|
P Ш |
Dwz ai dz awaт
Получим: (В)
Сравнение полученного уравнения (В) с исходным (А) дает возможность при наличии подобия определить значения ряда индикаторов подобия, а именно:
|
1 |
Для членов, учитывающих неустановившееся движение
А\ •
Для членов, учитывающих влияние объемных сил или силы тяжести
Agal ___ м
|
Гаг |
2 * а...
Для членов, учитывающих влияние гидростатического давления
= 1
А а:.
Для членов, учитывающих влияние сил внутреннего трения
А.,
_
Аи ару
Подставив в полученные индикаторы; подобия вместо масштабных множителей соответствующие отношения физических величин
(физические величины в числителе относятся к данной системе, а в знаменателе к подобной), получим четыре безразмерных комплекса или критерия jg
1. Критерий гомохронности (Но), учитывающий неустановившееся состояние движения жидкости, получается из индикатора подобия
Flz _ k _ ]
|
WZ W-.Z, . J = —~ = idem |
А„,а, wz
Откуда
І
— lx
WZ
~~Z=Ho _ (1—61)
Во всех системах, подобных данной, критерий гомохронности будет иметь одно и то же значение, если только в этих системах движение жидкости неустановившееся.
2. Критерий Фруда (Fr), учитывающий влияние* сил тяжести, получается из индикатора подобия
Gi
Agai ___ еА_____ і
А2 — W* —
W ----
|
©ткуда |
«?
4 «=^4 = idem
W*
%=Fr (1-62)
W
Чтобы избежать дробных величин, гобычно Пользуются обратным выражением:
|T=Fr (1—62а)
3. Критерий Эйлера (Ей), учитывающий влияние сил гидростатического давления, получается из^индикатора подобия
Р
Ар _ Рі ________ і
A al Р^2 ~
РіШ?
Откуда
Критерию Эйлера обычно придают несколько иной вид. Вместо величины абсолютного давления р вводят разность давлений Ар в каких - нибудь двух-точках жидкости, и критерий Эйлера принимает следующий вид:
= (1—63а)
|
= 1 |
4. Критерий Рейнольдса (Re), учитывающий влияние сил внутреннего трения в вязкой жидкости, получается из индикатора подобия
И Hi
Awata wl р
ЩІіРі
Откуда
Fx (Xj
^=Re (1-64)
Таким образом, уравнения Навье—Стокса движения вязкой жидкости, описывающие в общей форме процесс движения жидкости, в результате подобного преобразования могут быть представлены в виде функции от критериев подобия
Ф (Но, Fr, Ей, Re)= 0 (1—65)
Полученное выражение есть первообразная функция дифференциальных уравнений движения и является их интегралом или решением.
Вид этой функции определяется из опыта в зависимости от конкретных условий протекания жидкости.
Если рассматривается установившееся движение, то из уравнения (1—65) исключается критерий гомохронности и оно принимает вид:
Ф,(/7\ Ей, Re) = 0 (1—65а)
При установившемся движении идеальной жидкости, т. е. жидкости, протекающей без трения, уравнение (1—65а) видоизменится так:
Ф2(Fr, Еи) = 0 (1—656)
Полученное уравнение есть интеграл уравнений движения Эйлера. Вид этой функции определяется уравнением Бернулли.
14. Сопротивление в трубопроводах
Общие уравнения сопротивления. По предыдущемуТ(1—30) гидродинамический напор в сечении, где жидкость вытекает из трубопровода, выражается равенством 1
« = (А)
Потеря напора hn в трубопроводе обусловлена наличием сопротивлений, которые должна преодолеть протекающая жидкость на своем пути. Эти сопротивления бывают двух родов:
1) сопротивление трения жидкости о стенки;
2) местные сопротивления, возникающие при изменении направления движения жидкости или геометрической формы трубопровода.
При гидродинамическом напоре Н и отсутствии сопротивлений скорость протекания жидкости по трубопроводу выразилась бы величиной, равной скорости истечения:
Wq = Y 2gH м/сек
В реальных трубопроводах часть общего напора расходуется на преодоление сопротивлений, и действительная скорость w будет значительно меньше w0.
При фактической скорости протекания w, скоростной напор, т. е. напор, которым обусловливается скорость w, выражается величиной
H = — пск. 2 G
Представив сумму сопротивлений через отдельные составляющие
Hn = hm +hn2 +/zna + . . . + Кп
Можно гидродинамический напор по уравнению (А) выразить следующим образом:
Н ==~ + Hni + Hnt + Hm + • • • + HUn (1-66)
Сопротивления hni, hn2, h„3 ■•■ hu можно представить в долях от скоростного напора:
H —th — С —
11пі — 1ск - — --1 2 g
H —I h _C
'-П2 -- — -2 2g
H = t h =1 ~ "■пп ^ппск. Si 2g
Где величины Сх, С2, • • •, С„—это коэффициенты сопротивления, представляющие собой доли от скоростного напора, причем в общем виде коэффициент сопротивления равен
Г — Нп« Я h
''ск.
При этих условиях общий напор может быть выражен уравнением
И - -I - Г _ - Х - Г -1— 4- Г _
2G ^ 2G> 2g ґ [2G
Или окончательно
Н = ^(\+Щм (1—66а)
Сопротивление трения движению жидкости:
/*П = С|| (1-67)
Где ^—коэффицент сопротивления трения.
На основании закона Ньютона сила внутреннего трения движущейся жидкости зависит от ее вязкости и скорости движения, т. е. является функцией критерия Рейнольдса.
5 А. Г. Касаткин.
Очевидно также, что сопротивление трения жидкости о стенки трубопровода будет тем больше, чем длиннее трубопровод и. чем меньше его диаметр. Следовательно, в общем виде коэффициент сопротивления трения движущейся жидкости может быть выражен уравнением
С = ?(/?*) 4 (1-68)
Где Re—критерий Рейнольдса;
I—длина трубопровода в м\ d—внутренний диаметр трубопровода в м.
Подставив значение С из уравнения (1—68) в уравнение (1—67) и заменив Нп равной величиной (где Др—потеря напора, выраженная в кгс/м2 и у—уд. вес жидкости в кгс/м8), получим:
Дp = y(Re)J-J! Ј - Кгс/м2 (1—69)
Функцию <?(Re) в уравнении (1—69) называют коэффициентом трения. Обозначим ее через X, т. е.
X — ср (Re)
Тогда потеря напора на преодоление трения в трубопроводе выразится в окончательном виде уравнением:
= кгс/м2 (1—70)
Или
= кгс/м2 (1—70а)
Так как коэффициент трения X является функцией критерия Рейнольдса, то числовое значение етого коэффициента будет зависеть прежде всего от характера движения, и для ламинарного движения коэффициент трения будет иным, чем для турбулентного.
Сопротивление трения при ламинарном движении жидкости в трубах. При ламинарном движении значение функции X=®(/fe) легко найти теоретически, и коэффициент трения жидкости может быть выражен одной общей формулой.
Расход жидкости через трубу круглого сечения выражается равенством]
^сек. = МЧСЄК
Подставив это значение расхода в уравнение (1—55в), получим
4 W ~~ 128fx/
Решая последнее уравнение относительно разности давлений
А \ 32ixwl Pi — = =
И сопоставляя полученное с уравнением (1—70), выражающим потерю давления в общем виде
D 2g ~~' d2
Найдем коэффициент трения при ламинарном течении жидкости
, __ 64р.
|
Wdy wdp _ 64 — Re _ 64 I ~ Re d |
|
Или |
|
(1-71) (1-72) |
|
И коэффициент сопротивления |
Полученное уравнение выражает закон сопротивления трения при установившемся ламинарном течении жидкости в трубах.
Опытные данные определения потери напора строго подчиняются этому закону в пределах установившегося ламинарного движения жидкостей, т. е. в пределах значений критерия Рейнольдса ниже критического (/&<2320).
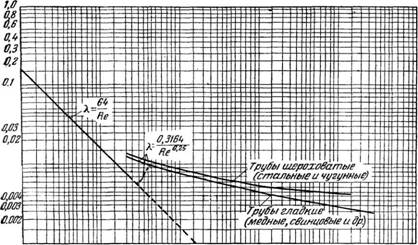
При критическом значении числа Рейнольдса ламинарное движение нарушается и возникает турбулентное движение, которое уже не подчиняется закону, выраженному уравнением (1—72). Если по уравнению (1—71) построить график в логарифмическом масштабе (рис. 14) и на-
|
|
|
0,08 А °'06 ~4 0,0't |
|
№ dm 0,006 |
|
0,001 |
|
WZ 2 ЗЬ56Ъ103 г ЗЬ56Ш* 2 ЗЬ568Ю5 2 ЗЬ56&Ю6 2 ЗЬ56ЪШУ Критерий Ре Рис. 14. Зависимость коэффициента трения от режима движения жидкости. |
Нести опытные данные, то получится прямая с постоянным углом наклона, на которую и ложатся точки в пределах ламинарного режима, т. е. в тех пределах, в которых применим закон сопротивления, соответствующий уравнению (1—72).
Из графика видно, что при значениях 2320 характер зависимости X от Re резко меняется, и для турбулентного движения приведенный выше закон сопротивления неприменим.
Здесь следует указать на общий принцип построения графиков, отражающих связь между критериями подобия, по которому был построен и график уравнения (1—71). Такими графиками приходится часто пользоваться.
Обычно связь между критериями подобия выражается степенной функцией вида
У = Ьхп
Логарифмирование которой дает
Lg у = lg n lg х
Обозначая
Lgy=Y\ lg b = B; \gx = X
Можно написать
Y = B+nX
Последнее выражение есть уравнение прямой, если оси координат построить в логарифмическом масштабе.
Вследствие этого построение связи между критериями подобия значительно упрощается, а график будет иметь небольшие размеры.
Сказанное выше относилось к ламинарному потоку жидкости в трубе круглого сечения.
|
А_ Re |
Если ламинарное движение происходит в трубах некруглого сечения, то коэффициент трения выражается уравнением
(1-73)
Где А—коэффициент, числовая величина которого зависит от формы поперечного сечения трубы (табл. 4).
Таблица 4
|
А |
57 |
|
0,58 а |
53 |
|
25 |
96 |
|
1,3а |
62 |
Значения эквивалентного диаметра d3KB. и коэффициента А для труб некруглого сечения
, Сечение трубы
Квадрат со стороной а........................................
Треугольник равносторонний со стороной а....
Кольцо шириной 8 .............................................
Прямоугольник со сторонами а и b (а=0,56)....
Формула (1—74) применима для числовых значений Re в пределах от 3-Ю3 до 1-Ю5. В области значений Re от 4-Ю3 до 6,3-106 для гладких труб применимо уравнение ВТИ:
(lg Ref[4]
В области значений ^?е>5000 можно пользоваться Филоненко:
? 0,303
|
(1-76) |
|
X: |
|
Уравнением (1-77) |
~~~{\gRe— 0,9)2
Формулы (1—73)—(1—77) справедливы для изотермических условий потока жидкости или газа.
В тех случаях, когда температура потока отличается от температуры стенки трубы, следует найденные по этим формулам числовые значения коэффициентов X умножить на величину k, равную: для ламинарного режима потока
|
Ргс |
|
(1-78) |
|
1 +0,22 |
|
K = |
|
Ргя |
Gr. Pr-M \o. i6
Rey
Для турбулентного режима потока
(1—78а)
Где ReM, Ргж и Єгж—критерии Рейнольдса, Прандтля и Грасгофа для данной жидкости при ее средней температуре и ReCT., Р/'ст. и Gact.—те же критерии для той же жидкости при температуре стенки трубы*.
Для случаев движения жидкости или газа внутри труб некруглого сечения коэффициент трения определяется по тем же формулам, что и для круглых труб, но в качестве линейного размера при подсчете числа Re принимается эквивалентный диаметр.
Для водяного пара практически в большинстве случаев с достаточной степенью точности можно принимать Х=0,03.
Влияние шероховатости стенок труб на сопротивление. При движении жидкости по трубам, не имеющим гладкой поверхности, как, например, по керамическим трубам с нешлифованной внутренней поверхностью, по загрязненным трубам и т. п., следует учитывать влияние шероховатости на величину X. В качестве характеристики шероховатости вводится понятие «относительной шероховатости» или «коэффициента шероховатости» п, представляющего собой отношение средней величины выступа шероховатости (или глубины впадины) г к радиусу трубы л, т. е.
П г
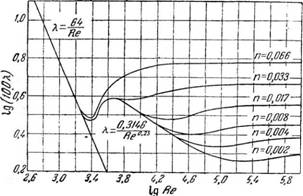
Зависимость коэффициента трения круглых труб от величины относительной шероховатости, найденная опытным путем с применением метода подобия, представлена на рис. 15.
|
РгГТ. \ |
Установлено, что:
1. Коэффициент трения при ламинарном движении (Re<2320) практически не зависит от шероховатости труб, а только от числового значения Re и определяется по формуле (1—71).
2. Переход от ламинарного к турбулентному движению (Re>2320) сопровождается увеличением коэффициента трения. В этом случае на величину коэффициента трения влияет шероховатость; и чем больше шероховатость, тем больше коэффициент трения.
|
Рис. 15. Зависимость коэффициента трения от относительной шероховатости труб и критерия Рейнольдса. |
Однако в пределах значений критерия Рейнольдса
Сопротивление шероховатых труб не отличается от сопротивления гладких труб.
В этой зоне значений Re для определения следует пользоваться уравнениями (1—74)—(1—77).
При дальнейшем увеличении турбулентности начинает заметно сказываться и влияние шероховатости.
3. В последующем коэффициент X достигает максимального значения и с изменением величины Re не меняется. Это постоянное значение X зависит от Re (так, например, для «=0,066 коэффициент трения ^=const достигается при Re^ 100 000).
В этой зоне значений Re гидравлическое сопротивление пропорционально квадрату скорости, и коэффициент трения для шероховатых труб может быть определен по формуле
^ = ^1,74 + 2 lg ~j~2 (1—79)
Или
|
( |
Г \-0,25
(1—79а)
Значение Re, при котором коэффициент Трения становится постоянной величиной, может быть ориентировочна принято
Re=m-
Є
При определении коэффициента трения для шероховатых труб можно вместо формулы (1—79) пользоваться также формулой
/ є \0,25
X = 0,111 (-^j (1-796)
Значения є зависят от материала трубы, а также от режима протекания в ней жидкости и могут быть приняты ориентировочно равными (в мм): для новых чугунных труб s«=0,3; для старых чугунных и керамических труб є=0,86—1,0 и для новых стальных цельнотянутых труб и оцинкованных труб s=0,l—0,2 (при протекании жидкостей, вызывающих сильную коррозию, є=0,8).
Местные сопротивления. При определении потери напора необходимо учитывать и местные сопротивления (в сужениях, на расширении и закруглении труб, в кранах, вентилях и др.). Коэффициенты местных сопротивлений определяют опытным путем.
Ниже приведены значения коэффициентов некоторых наиболее часто встречающихся местных сопротивлений.
|
F |
1. Вход в трубу. Коэффициент местного сопротивления в этом случае зависит от формы входной кромки трубы. Если края острые (рис. 16, /), то С=0,5, если же они тупые, то С=0,25. При закруглен-
|
Рис. 16. Формы входной кромки Рис. 17. Внезапное расширение (/) и сужение (//) Трубы: трубы, /—края острые; II—кромка закруглена. |
|
' п 1 II |
Ной кромке трубы (рис. 16, II) величина С в зависимости от радиуса закругления и шероховатости стенок трубы колеблется в пределах 0,06—0,005.
2. Выход из трубы. Коэффициент местного сопротивления может быть принят С=1.
3. Внезапное расширение трубы (рис. 17, /). В этом случае коэффициент местного сопротивления зависит от отношения узкого сечения fj трубы К ее широкому сечению f* и может быть принят равным:
/х: f2 . . . 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 : 0,81 0,64 0,49 0,36 0,25 0,16 0,09 0,04 0,01 0
При расчете потери напора следует учитывать, что приведенные выше значения С отнесены к скорости в узком сечении трубы
4. Внезапное сужение трубы (рис. 17, II). Коэффициент местного сопротивления при внезапном сужении трубы зависит от отношения узкого сечения /2 трубы К ее широкому сечению /j. Ниже приведены значения С, отнесенные к скорости в узком сечении трубы:
/,:/! . . . 0,01 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
:.............................. 0,5 0,47 0,45 0,38 0,34 0,3 0,25 0,2 0,15 0,09 0
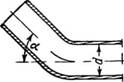
5. Колена в трубах. Коэффициенты местных сопротивлений колен зависят от угла наклона а (рис. 18) и шероховатости стенок колена (табл. 5).
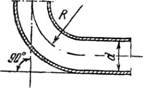
6. Закругления труб (отводы). Для закругления или отвода круглого сечения (рис. 19) коэффициент местного сопротивления определяют по формуле
С = |о, 131 + 0,16 (4-)S,6]w (1"80>
|
Таблица 5 Коэффициенты местного сопротивления в коленах
|
|
Рис. 19. Отвод. |
Подставив в формулу(1—80) разные значения-^-при и=90°, получим
D_
|
Рис. 18. Колено. |
|
R 0,25 0,4 0,6 0,8 1 0,13 0,14 0,16 0,20 0,29 |
R С.
|
На практике закругления |
Для наиболее часто применяемого (R=4d) коэффициент С «=0,13.
|
|
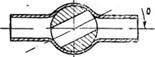
Рис. 20. Дроссельный клапан (а) и проходной кран (б).
Коэффициент местного сопротивления на закруглении (отводе) прямоугольного сечения определяют по формуле
|
D \3'6 |
|
К W |
|
(1-81) |
С = [0,124 + 0,274
7. Дроссельный клапан. Коэффициент местного сопротивления зависит от угла а открытия клапана (рис. 20, а) и может быть принят равным:
А° .... 5 10 20 30 40 45 50 60 70 С 0,24 0,52 1,54 3,91 10,8 18,7 32,6 118 751
8. Проходной кран. Сопротивление в проходном кране зависит от угла а поворота (открытия) пробки крана (рис. 20,6). Значения коэффициента местного сопротивления принимают равными:
А° .... 5 10 С 0,05 0,29
20 30 40 45 50 60 65 1,56 5,47 17,3 31,2 52,6 206 486
Принимать следующие средние значения коэффициента местного сопротивления: для нормального вентиля для косого вентиля С=1,40—1,85, для прямоточного вентиля С=0,5—0,8, для задвижки, параллельной с выдвижным шпинделем, С=0,15.
В инженерной практике часто учитывают местные сопротивления, приравнивая их к потерям напора на трение [см. формулу (1—70)] в прямой трубе длиной /экв.. Эквивалентную длину определяют в виде произведения некоторого коэффициента на внутренний диаметр трубы d, выраженный в метрах. Например, для колена с углом наклона 90° и d=9+60 мм /экв. = 30 d, для тройников приб/=25+100 мм /экв.=60+90 d, ДЛЯ Крестовин ^экв.== 50 d и т. д.
Если опытные значения коэффициентов местных сопротивлений известны, то, определив расчетом величину коэффициентов сопротивления, можно рассчитать гидравлическое сопротивление аппаратуры по общей формуле (1—66а).
Краткие сведения по гидравлическим расчетам некоторых распространенных аппаратов, например теплообменников и насадочных колонн, приведены в соответствующих главах книги.