Плотность и структура геля
Манегольд [127] рассматривал типы структур и упаковок, получающихся при регулярном расположении элементов сетки
Геля, когда изменяется «координационное число» частиц кремнезема, т. е. число частиц, связанных с данной частицей. В наиболее плотно упакованных гелях каждая отдельная сферическая частица соприкасается с 12 окружающими ее сферами, и в этом случае доля объема, занимаемая сферами, S равна 0,745. В случае наиболее открытой регулярной структуры сетки геля, показанной на рис. 3.27, каждая сферическая частица связывается с тремя другими сферами (т. е. «координационное число» равно трем) и величина S составляет только 0,05.
|
Щщ |
|
|
|
Рис. 3.27. Упаковка сферических частиц с «координационным числом» 3. (По данным Айлера [89] с разрешения Cornell University Press.) |
Однако частицы также могут образовывать короткие цепочки, в которых «координацион - і ное число» равно двум. Таким образом, в любом ряду частиц, образующих сетку, «координационные числа» меняются как 3, 2, 2, 3, 2, 2 и т. д., причем доля объема S составляет 0,0083. Этот случай, показанный на рис. 3.28, должен соответствовать гелю, сформированному из золя с содержанием кремнезема 0,83 % Si02 по объему или 1,8 % по массе. Тем не менее в случае достаточно маленьких частиц золь кремнезема способен образовывать слабую, но непрерывную по всему объему сетку геля даже при содержании в золе 1 % Si02 и менее. Тогда «координационные числа»
|
|
|
Рис. .3.28. Упаковка сферических частиц с «координационными числами» 3, 2, 2, 3. Каж- |
|
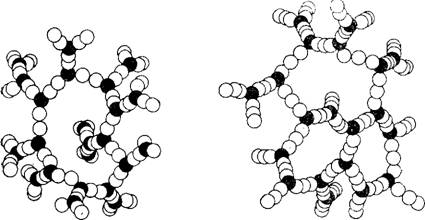
Рис. 3.29. Сетка геля, состоящая из частиц с «координационными числами» 3, 2, 2, 2, 3. |
|
Дая сфера, помеченная черным, связана тремя другими. |
Могут составлять ряд: 3, 2, 2, 2, 3 и т. д. Модель подобной очень открытой сетки со средним значением «координационного числа», соответствующим последнему случаю, показана на рис. 3.29.