ХАРАКТЕР ВЗАИМОСВЯЗИ МЕЖДУ ПОЛЗУЧЕСТЬЮ И ПРОЧНОСТЬЮ БЕТОНА
Попытки отыскать такую взаимосвязь неоднократно предпринимались в последние годы. Первая из них была сделана в 1950 г. в Цюрихской лаборатории испытания материалов [199]. Предельное значение меры ползучести неармированного бетона произвольного состава при за - гружейии его в возрасте 28 суток было предложено оценивать по формуле
Cm(28) = -|, (VI.7)
Где R — кубиковая прочность бетона в возрасте 28 суток; ki — безразмерный коэффициент, зависящий от относительной влажности среды 0. Например, при 0 = 70% h = =2500 • Ґ0-6.
Позднее эта формула была уточнена по предложению Вёльми [1991:
Ст(28) = ».Д/Д(Д + 0.33Ц) f (VI.8)
R
Где В и Ц — весовые расходы воды и цемента на 1 м3 бетонной смеси; — коэффициент, числовое значение которого для указанных выше условий влажности воздуха составляет 14 • Ю-6.
В 1959 г. А. Гуммель на основании результатов своих опытов с бетонами одинакового весового состава [157] предложил оценивать предельное значение меры ползучести бетона по формуле
Cm( (Vi.9)
R /(Rm/R)*
Где Vn — содержание пор по объему в цементном камне бетона, вычисляемое в предположении, что химически связанная вода составляет 15% веса цемента; Rm—предельное (при T оо) значение кубиковой прочности бетона; k3 — безразмерный коэффициент, который для условий опытов Гуммеля (г — 5 см, 0 = 65%) оказался равным 94 • Ю-6.
Рекомендации Европейского комитета по бетону [96] также позволяют представить меру ползучести в виде выражения, которое содержит в качестве одного из параметров марочную прочность бетона:
Ст(28) = --- , (VI. 10)
Где — коэффициент, зависящий от размеров сечения элемента и влажности окружающей среды. Например, для принятых исходных условий (г = 2,5 см, 0 = 70%) = = 0,92 - Ю-6.
Сравнивая рассмотренные выражения, приходим к выводу, что для одного и того же бетона и прочих равных условий они по-разному оценивают величину меры ползучести. В табл. И в качестве примера приведены расчетные значения Ст(28) по формулам (VI.7) — (VI. 10) для ориентировочных составов бетона марок 200, 400 и 600 в условиях загружения, принятых за исходные (г = 2,5 см, 0 = 70%, т = 28 суткам)[2].
|
Таблица 11
|
Расхождения в величинах Ст(28) для бетона заданной прочности будут сохраняться и при любых других возможных вариантах дозировки составляющих для получения бетона данной марочной прочности.
Аналогичные несоответствия обнаружены и в других известных в настоящее время рекомендациях, устанавливающих численные соотношения меры ползучести тяжелого бетона и его прочности (без учета других технологических параметров). Предлагаемые зависимости Cm(28) —f(R), сопоставленные между собой применительно к одинаковым исходным условиям загружения бетона, различаются не только количественно, но и качественно (см., например, кривые 3 и 4 на рис. 48).
Большинство рассмотренных зависимостей, как аналитических (табл. 11), так и в численной форме (рис. 48), относятся к бетонам обычной прочности (марки до 600). Трудно судить, в какой мере они применимы для бетонов
Высоких прочностей, тем более что попытка экстраполировать соответствующие зависимости в эту область приводят к разным результатам. В то же время надежное прогнозирование деформаций высокопрочного бетона возможно лишь при наличии устойчивой корреляционной связи
|
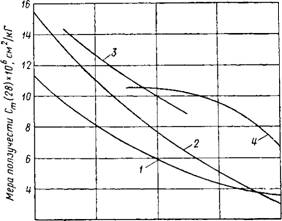
200 300 400 500 600 Рис. 48. Мера ползучести тяжелого бетона Ст(28) в зависимости от его марки R (приведенный радиус сечения элемента г = 2,5 см, относительная влажность воздуха 0= 70%, возраст в момент загружения т = 28 суткам) по данным ЦНИИС (1962 г.) [И]; 2 — Серегина [79]; 3 — Иванса и Конга [135]; 4 — комиссии ФИП [137] |
|
/?, кг/смг |
Между ползучестью тяжелого бетона и его прочностью в широком диапазоне изменения последней.
При анализе данных табл. 11 и рис. 48 возникает вопрос о том, насколько универсальны непосредственные связи такого рода для любого тяжелого бетона рассматриваемой категории. Существующие точки зрения на этот счет весьма противоречивы.
По мнению А. В. Саталкина [78], Невилля [171], Кли- гера [163], деформативная способность бетона закономерно уменьшается по мере роста его прочности в момент загружения (т. е. в данном случае марочной прочности). И. Н. Серегин [79] пришел к выводу, что марка тяжелого бетона сама по себе позволяет достаточно надежно судить
JJ9
О свойствах ползучести этого материала, и влиянием других технологических параметров можно пренебречь. По мнению других исследователей, в частности Лермита [52], форма соответствующей связи далеко не доказана, поскольку систематические исследования в этом направлении отсутствуют. И. И. Улицкий [94], утверждает, что прочность бетона вообще не может служить критерием для оценки свойств ползучести.
Однако экспериментальные результаты формально не дают достаточных оснований для любого из этих утверждений. В опытах Гуммеля [157] испытанию на ползучесть подвергались, например, два различных состава бетона ( на разных цементах), имеющего примерно одинаковую куби - ковую прочность в 28-суточном возрасте (504 и 519 кГ/см2). У образцов, загруженных в этом возрасте, через 1100 суток обнаружена различная ползучесть (мера ползучести 5х 10_6 и 8х 10~6 соответственно). В то же время в подобных испытаниях Хансона [150] ползучесть бетона двух составов, приготовленного на разных цементах и имеющего примерно одинаковую кубиковую прочность (485 и 550 кГ/см2), оказалась через 1000 суток также примерно одинаковой (мера ползучести 10,9 х 10~6 и 10,3 X Ю-6). Аналогичные результаты получены в опытах Уоша [205].
Отмеченные противоречия и расхождения не нашли до настоящего времени удовлетворительного объяснения. Учитывая характер влияния важнейших технологических факторов на ползучесть тяжелого бетона и его прочность, попытаемся проследить принципиальную форму взаимосвязи этих характеристик материала. Для этого проанализируем значение меры ползучести бетона в принятых исходных условиях загружения (г = 2,5 см, 8 = 70%,
% = 28 суток), полагая в выражении (VI. 1)
= =
Т. е.
Cn = Cm(28)=Q„(28)K& (VI.11)
Где Сн — так называемое нормативное значение меры ползучести, отражающее совместное влияние трех главных технологических параметров ВІЦ и рт) при прочих одинаковых условиях.
Подставляя в выражение (VI. 11) эмпирические зависимости (VI.2), (VI.3) и (VI.4), а также используя из-
В работе [1101 было показано, что числовые значения функции цементоводного отношения г (в квадратных скобках) при изменении аргумента в возможных пределах 2 = 1,54-3,25 (В/Ц= 0,3-^0,7) остаются практически неизменными и составляют 1,10—1,12. Влияние активности цемента R ц при заданной прочности бетона R также незначительно для любой из существующих марок портланд
От 1,25 —1,50. И в том, и в другом случае можно оперировать средними значениями обеих указанных функций, допуская максимальную погрешность не более ±10%. Принимая также среднее значение коэффициента А = 0,56, рекомендуемое для бетона на материалах среднего качества [82], удается свести выражение (VI. 12) к весьма простой зависимости:
|
|
(VI.13)
Где R — кубиковая прочность (марка) бетона в 28-суточ - ном возрасте; В — расход воды в литрах на 1000 л ( 1 м3) Бетонной смеси: Kn — постоянный безразмерный коэффициент, равный примерно 16х10~6.
Точно такой же результат получается [110], если оперировать значениями активности цемента Rn по старому ГОСТ 310—41.
Таким образом, в силу определенных взаимозависимостей трех главных технологических параметров бетонной смеси их суммарное влияние на ползучесть бетона может быть учтено через две независимые характеристики — марку бетона R и расход воды в бетонной смеси В. Преимущества данного пути с точки зрения упрощения методов оценки деформаций ползучести и удобства использования этих методов очевидны.
|
|
|
Цемента (300—600). Величина функций изменяется |
|
Вестное соотношение (1.1) для марочной прочности бетона R, получим
|
|
(г—0,5) (1+г)1 |
|
(VI. 12) |
Выражение (VI. 13) положено в основу методики оценки величины деформаций ползучести тяжелого бетона марок 150—600, рекомендованного «Указаниями по проектированию железобетонных мостов» СН 365—67 [92].
На основании полученного выражения (VI. 13) с учетом экспериментальных данных о влиянии старения бетона на деформации] ползучести (см. главу VIII) удается сформулировать [110] общее положение о характере связи между величиной меры ползучести бетона Ст(т) при загружении в произвольном возрасте т и его абсолютной прочностью Rx В том же возрасте. Подстановка эмпирического выражения (VIII.2), приведенного в главе VIII, в формулу (VI. 13) после несложных преобразований дает
(VI. 14)
Числовые значения функций в квадратных скобках весьма близки к единице при изменении аргумента Rx/R в диапазоне 0,7 ^ Rx/R ^ 1 и резко уменьшаются вне указанного диапазона. Таким образом, лишь при выполнении условия 0,7 ^ R%/R ^ 1
(VI.15)
И, следовательно, мера ползучести бетона может быть связана с его абсолютной прочностью в момент загружения Rx Только на определенной стадии твердения. Именно благодаря этому можно пользоваться формулой (VI. 13), представляющей частный случай выражения (VI. 15) при Rx = R.
При загружении бетона на более ранних или более поздних стадиях процесса твердения связь в форме (VI. 15) уже не прослеживается. При Rx/R < 0,7 оценка деформаций ползучести по абсолютной прочности бетона Rx Привела бы к их завышению за счет неучитываемого существенного влияния роста прочности после приложения нагрузки. При Rx/R > 1 возможно аналогичное явление, но уже за счет превалирующего влияния изменения гигро- метрического состояния твердеющего бетона (см. главу VIII). В пределах 0,7 ^ Rx/R ^ 1 действие обоих указанных факторов, по-видимому, таково, что оно взаимно уравновешивается.
|
|
Однако и в последнем случае, как следует из выражений (VI. 13) и (VI. 15), никакой однозначной зависимости между мерой ползучести бетона и его прочностью в момент загружения не существует. Эта зависимость представляется в виде серии гиперболических кривых, каждая из которых соответствует определенному постоянному расходу воды
в смеси. Поэтому нормирование деформаций ползучести различных по составу бетонов (даже при прочих равных условиях) в функции только их прочности является методически неправильным и неизбежно приводит к разноречивым результатам (см. рис. 48).
В выражении (VI. 13) это обстоятельство учитывается тем, что наряду с прочностью R здесь используется второй независимый параметр — расход воды в смеси В. Сравним полученное выражение с приведенными ранее аналитическими зависимостями (VI.7)—(VI. 10) применительно к одинаковым исходным условиям загружения бетона и попытаемся выяснить, чем обусловлены различия в форме этих зависимостей.
Формулы Вёльми (VI.8) и рекомендаций ЕКБ (VI. 10) можно рассматривать, как выражение (VI. 13), в котором наряду с множителем B/R вместо постоянного коэффициента kn фигурируют некоторые функции:
В формуле Вёльми (VI.8) k'n = 14(Ј/Z(+ 0,33) 10"6;
В формуле ЕКБ (VI. 10) ^-0,92/^(В/Д + 0,33)10~6.
Легко установить, что возможное в обычных пределах изменение числовых значений K'N и K"N оказывает по сравнению с множителем B/R второстепенное влияние на результаты подсчетов по обеим формулам. Эти значения достаточно близки к величине коэффициента Kn = 16 • Ю-6 в формуле (VI. 13), однако в формуле Вёльми они уменьшаются, а в формуле ЕКБ, напротив, увеличиваются по мере повышения марочной прочности бетона (наилучшее совпадение с Ku = 16 • Ю-6 получается соответственно у бетона низких или высоких марок). Наиболее стабильны при этом значения k"n в формуле ЕКБ, поскольку входящие в него параметры В/Ц и ]/"/? изменяются при прочих равных условиях взаимно противоположно.
Таким образом, формулы Вёльми и особенно ЕКБ в неявном виде отражают по существу те же принципиальные связи, что и выражение (VI. 13), но в более сложной форме (при переменных коэффициентах k'n и k'n). Зависимость (VI. 13) с постоянным значением коэффициента позволяет оправданно упростить практические расчеты, кроме того, она больше соответствует экспериментальным закономерностям (см. табл. 13).
Что касается формул Цюрихской лаборатории (VI.7) и Гуммеля (VI.9), то они представляют собой не более как частные случаи выражения (VI. 13).
Первая из них получается, если принять в формуле (VI. 13) 155 л! мг. Поэтому формула (VI.7) может давать удовлетворительные результаты лишь при оценке деформаций бетонов разной прочности, имеющих указанную постоянную дозировку воды.
Формула Гуммеля практически не отличается от выражения (VI. 13), если записать последнее применительно к конкретной величине расхода цемента в исследованных Гум - мелем бетонах (Ц ж 340 кг1мв = const), т. е. представить (VI. 13) в виде
Г 1П6_ 16-330В/Ц 5 44ОВ/Ц Сн'Ш R R '
Одновременно преобразуем формулу Гуммеля, учитывая, что входящее в нее значение пористости цементного камня Va для обычного диапазона изменения ВІЦ = 0,34-0,6 Примерно пропорционально этой величине, т. е. Va(%) ж « 0,8 ВІЦ • 100. Отношение Rm/RВ той же формуле колеблется обычно в узких пределах Rm/R =1,24-1,5 (см. главу VIII). С учетом этих соображений формула Гуммеля принимает вид
94-0,8В/Д. 100 (5 800 ~6 600)5/Д
Г (9R. 106 — =;_____ ; '
І" (1,13 - г 1,30)R R
(т. е. полностью совпадает с предыдущим выражением не только по форме, но и порядку величин). Поэтому формула Гуммеля (VI.9) может быть использована только для оценки деформаций бетонов с неизменным расходом цемента порядка 350 кг/м2.
Таким образом, полученное выражение (VI. 13) является наиболее простой и в то же время достаточно общей зависимостью деформаций ползучести от прочности бетона для тяжелых бетонов рассматриваемой категории.
Можно ожидать, что для высокопрочных бетонов наиболее близкие результаты при оценке величины деформаций могут быть получены по формулам (VI. 13) и ЕКБ. Формулы Гуммеля и Вёльми мало пригодны в этом случае и будут давать заниженные значения деформаций.