ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ

АНАЛИЗ И ОПТИМИЗАЦИЯ ГЕЛИОУСТАНОВОК МЕТОДАМИ ТЕОРЕТИКО-ГРАФОВЫХ ПОСТРОЕНИЙ

10.1. ГЕЛИОУСТАНОВКИ С СЕЗОННЫМ АККУМУЛИРОВАНИЕМ ЭНЕРГИИ

Изучение сложной системы, каковой является энергос­берегающая установка, предполагает ее представление в виде модели, позволяющей выполнить анализ поведения системы при различных внешних воздействиях. Следует подчеркнуть, что свойства элементов могут изменяться в процессе действия системы в целом. Оптимизацию изучае­мых явлений нужно основывать на методе системного ана­лиза, который ориентирует исследования на раскрытие це­лостности объекта и взаимосвязи его основных элементов.

Решение этих задач невозможно без математического моделирования. Реализация соответствующих математи­ческих моделей на ЭВМ позволяет проводить анализ и по­иск наиболее обоснованных проектных решений.

При проведении системного анализа целесообразно об­ратиться к методам теории графов. Теоретико-графовые методы весьма результативны при анализе и синтезе си­стем энергосбережения [129,130].

Технологическую схему системы можно изобразить в виде потокового графа G(A, Г), где вершины - это элемен­ты схемы, а дуги - физические потоки (термодинамиче­ские параметры, потоки массы, теплоты, энергии) между элементами.

Для анализа энергосберегающих систем обратимся к параметрическому потоковому графу (ППГ) и к эксергети - ческому потоковому графу (ЭПГ).

Параметрический потоковый граф является топологи­ческой моделью системы. При построении ППГ создается информационная схема по технологической схеме и далее представляется в цифровой форме. Цифровым описанием выступает матрица инциденций, которая полностью отра­жает топологическую структуру информационной схемы и позволяет перенести эту структуру на язык алгебры или теории множеств.

Эксергетический потоковый граф учитывает не только параметры системы, но и потоки эксергии. Под ЭПГ следует понимать граф Е(А, Г) = Е(А, U), множество А = {аг а2,.... ак} вершин которого соответствует эксергетическим потерям в отдельных элементах системы, множество дуг U = {ир.... Uj}, k Ф I - распределению эксергетических потоков в системе;

Г - многозначное отображение множества А в себя. ЭПГ по аналогии с ППГ представляют в матричном виде.

На рис. 1.57 изображена схема системы теплохладос­набжения с адсорбционным термотрансформатором. Ис­точником энергии служит солнечное излучение. Данная схема предназначена для работы летом, поэтому термо­трансформатор используется в режиме кондиционирова­ния [131].

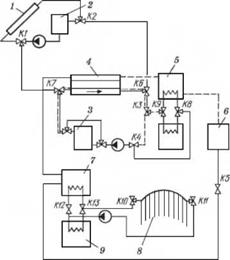Рис. 1.57.

Схема гелиоустановки с се­зонным аккумулированием энергии:

1 - солнечный коллектор; 2 — бак - аккумулятор солнечного конту­ра; 3 - бак-аккумулятор вторич­ного контура; 4 — теплообменник; 5, 7 - конденсаторы теплового насоса; 6 - расходный бак; 8 - се­зонный аккумулятор теплоты; 9 - испаритель

В ночное время суток хладагент из испарителя посту­пает в адсорбер. Теплота адсорбции отводится в грунто­вый аккумулятор-теплообменник. Часть вырабатываемо­го холода направляется потребителям, а остальная часть аккумулируется.

В дневное время используется холод, аккумулирован­ный в грунтовом теплообменнике.

Адсорбционные установки с твердым сорбционным по­глотителем имеют ряд преимуществ. Они не имеют движу­
щихся частей, не используют электроэнергию, просты в обслуживании.

В качестве сорбционных веществ используются цеоли­ты и силикагели. Более высокая сорбционная емкость до­стигается при применении в качестве адсорбента солей, на­пример, соединения СаС12 -2СН3ОН.

Основным термохимическим циклом СаС12—2СН3ОН в солнечной системе теплохладоснабжения будет следую­щий: солнечная энергия используется для разложения СаС12-2СН3ОН на СаС12 и пар при давлении около 300 мм рт. ст. Пар конденсируется при температуре 40 °С. Теплота конденсации может быть использована для нагрева воды, используемой на бытовые нужды. Этим завершается цикл генерации. Затем соль, отделенная от метанола, охлаж­дается и снова вступает в реакцию с паром. Жидкий ме­танол при испарении может охлаждаться до -25 °С. Обра­зующийся холод используется в системе хладоснабжения потребителей.

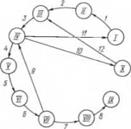На рис. 1.58 приведены параметрический потоковый граф анализируемой схемы и соответствующая матрица инциденций.

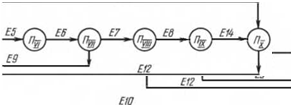Эксергетический потоковый граф и матрица инциден - ций схемы, показанной на рис. 1.57, изображены на рис. 1.59.

Сканируя по матрицам инциденций для ППГ и опреде­ляя булеву переменную на своем пути, ЭВМ рассчитывает все необходимые данные и находит значения параметров в данной узловой точке графа, значения тепловых и массовых потоков, условия оптимальной топологии схемы. Анало­гично по матрице ЭПГ ЭВМ вычисляет значения эксергии, эксергетических потоков и, следовательно, определяет сте­пень энергетического совершенства системы.

Математическая модель анализируемой системы тепло­снабжения или отдельных ее элементов может быть пред­ставлена в виде функционального оператора

где і - коды элементов (1, 2,п); Yt - вектор выходных па­раметров і-го элемента; Фг - вектор параметров функцио­нальных характеристик системы; дГ, , /£~ - нелинейные

вектор-функции i-ro элемента; X] - вектор входных вну­тренних параметров i-ro элемента; zTt — вектор режимных параметров і-го элемента; К - вектор конструктивных параметров і-го элемента: ТГ - топология подключения і-го элемента; Z - нелинейная функция критерия эффек­тивности; |/ - вид уравнения состояния; р, Т, h, s, р - со­ответственно давление, температура, энтальпия, энтропия, плотность рабочего тела; £, - параметр фазового превраще­ния в термотрансформаторе, для компрессионного тепло­вого насоса £ = 1.

Топология подключения і-го элемента определяет его место в схеме и его математическое описание по і-му ходу.

Уравнение баланса расходов і-го элемента:

= (1.259)

і=1

Уравнение баланса компонента для смеси рабочего тела теплового насоса:

Z Gjm^O. (1.260)

/=і

Уравнение баланса энергии і-го элемента с учетом топо­логии схемы:

+Nt=0. (1.261)

і=і

где Nt - внешняя энергетическая нагрузка на і-й элемент.

Уравнение гидравлического баланса потока в і-м элементе

^Р^ + Щ = 0. (1.262)

/=і

Изменения энтальпии потока в і - м элементе

j=h

^А/77іу + ДАу = 0. (1.263)

/=і

В этих уравнениях приняты обозначения: G - расход ра­бочего тела; APj - потери давления в данном элементе; ДЛу - изменение энтальпии раствора; пг. у - матрица инциденций.

Структурный анализ и оптимизация исходной много­контурной схемы основывается на следующем. Схемы представлены в виде параметрических графов, содержа­щих р разнопараметрических дуг S = (Sv S2, ..., S ) и и простых контуров (Lj, L2, ..., Lu). Необходимо в исходном параметрическом потоковом графе определить множе­ство особых дуг S* = (S1, S2, .... Sp), S* cz S, S* = p, p й и с минимальной суммой параметричностей. При этом не существует никакого другого подмножества R a S, R Ф S*, обладающего тем же свойством. Минимальная сумма пара­метричностей определяется соотношением р = min.

С энергетической точки зрения оптимум решения опре­деляется условием минимальных потерь эксергии:

^ПА=тіп. (1.264)

Изложим основные принципы синтеза энергосберегаю­щих систем.

Анализ схем энергосберегающих систем позволил уста­новить дискретность изменения параметров, структуру схемы и состав оборудования, нелинейность взаимосвязей между ними, нелинейность целевой функций и ограниче­нии. Поэтому данная задача является нелинейной задачей дискретной оптимизации. В качестве целевой функции могут быть приняты различные характеристики системы: технологические, энергетические, экономические и др. Будем исходить из того, что критерием оптимизации явля­ется энергетический показатель.

Пусть дан граф G(X, Г) = G(X, U), где X = {х.}, і = 1, 2, ..., п - множество его вершин, соответствующих некоторым численным значениям граничных и промежуточных зна­чений параметра. Задача заключается в том, чтобы найти кратчайший путь (по минимуму суммарного веса входя­щих в него дуг), т. е. минимизировать функцию

(1-265)

і і

для всех і и у, принадлежащих сети, і є х, у є х, і = 1, 2,..., п; j = 1, 2, ..., п - номера вершин; EL. - вес дуги і, /, т. е. за­траты первичной эксергии, соответствующие данной дуге;

1, если дуга i, j входит в рассматриваемый путь; О, в противном случае.

Граничные условия

1, k~s (источник), s-x0; О, для всех остальных хк ; -1, для k~t (сток), t~xn.

Сформулированная задача - это комбинаторная за­дача целочисленного дискретного программирования с булевыми переменными. Множество вершин X = {xj, i = l,2,..., п, формируется эвристически, исходя из опыта программирования.

Аналогично решается задача, если целевой функцией является один из экономических показателей.

Один из результативных методов оптимально­го синтеза энергосберегающих систем основывается на декомпозиционно-поисковом принципе. При этом возмож­ны несколько видов декомпозиции. Наибольший интерес представляет перспективно-отсекающая декомпозиция. Суть ее заключается в поиске оптимального решения Р* в подмножестве допустимых или перспективных решений {22}, т. е. Р*є {Е} с= {Р}, где {Р} - множество всех решений.