ТЕПЛОТЕХНИЧЕСКИЕ И ЗВУКОИЗОЛЯЦИОННЫЕ КАЧЕСТВА ОГРАЖДЕНИЙ ДОМОВ ПОВЫШЕННОЙ ЭТАЖНОСТИ
МЕТОДИКА РАСЧЕТА ПЛОСКИХ ТЕМПЕРАТУРНЫХ ПОЛЕЙ ЛЕГКИХ ОГРАЖДЕНИЙ
Все методы расчета плоских стационарных температурных полей ограждающих конструкций базируются на решении системы дифференциальных уравнений Лапласа. Однако теоретическое решение этой системы для плоских сечений современных конструкций в реальных условиях внутреннего и внешнего климатических воздействий неосуществимо, а решение математических уравнений с упрощениями не имеет практического значения. Главная трудность на пути таких исследований в сложности конфигурации узлов, а также в том, что в непрерывности значений теплопроводности на границе двух различных материалов возникают разрывы. В связи с этим в практике теплотехнических расчетов стали широко применять метод электротепловой аналогии, основанный на подобии явлений электро - и теплопроводности [16, 41, 45].
Распространенной электрической моделью с сосредоточенными параметрами являются устройства типа электроинтегратора Гутенмахера. Применение электроинтеграторов резко облегчило задачу расчетов температурных полей. Рассчитать плоское стационарное температурное поле на электроинтеграторе ЭИ-12 можно для сечения ограждающих конструкций любой конфигурации и при любых условиях тепло - и воздухообмена. Расчет отличается простотой подготовки исходных данных и наглядностью процесса решения задачи, что делает электромоделирующие устройства доступными и популярными среди инженеров-строителей. Однако точность расчетов на таких устройствах ограничена диапазоном омических сопротивлений (например, для ЭИ-12 от 0 до 100 Ом). Решение задач со сложной конфигурацией узлов и с материалами, имеющими большое соотношение значений теплопроводности (до 104) сильно осложняется, а иногда становится неосуществимым. Последнее относится к расчету легких ограждающих конструкций из алюминия и высокоэффективных утеплителей. Теплопроводность алюминиевых сплавов имеет порядок значений 2-102, а утеплителей — до 2-10~2 (отношение этих величин составляет 104). Поэтому и существующие методы расчета плоских температурных полей нуждаются в пересмотре и дальнейшем совершенствовании.
Универсальным методом решения системы уравнений Лапласа является конечно-разностный метод. Сущность его заключается в том, что вместо решения системы дифференциальных уравнений решают соответствующую ей систему уравнений в конечных разностях, которая получается либо благодаря замене производных их выражениями через конечные разности, либо составлением элементарных тепловых балансов. На основании построенной таким способом системы алгебраических уравнений до появления современных счетно-мо- делирующих устройств расчет выполняли вручную [45] с большими затратами труда и времени. Электронно - вычислительные машины позволили легко преодолеть трудности таких расчетов и, в свою очередь, дали сильный толчок развитию методов теории конечных разностей. В настоящее время разработаны самые разнообразные экономичные разностные схемы сложных физических задач и эффективные методы их практической реализации [11].
Для расчетов двумерных стационарных температурных полей плоских сечений ограждающих конструкций разработаны методика и программа на ЭВМ (см. приложение), основанные на методе конечных разностей. Разработка их преследовала две цели: во-первых, необходимо было, чтобы методика позволяла решать тот круг задач, который обычно решается с помощью электроинтеграторов, исключая такие характерные для последних недостатки, как ограничение в диапазоне значений теплопроводности; во-вторых, нужно было сохранить простоту и наглядность подготовки исходных данных, анализа окончательных результатов, характерные при работе с электромоделирующими устройствами.
Предлагаемая методика универсальна, т. е. предназначена для расчета двумерного стационарного температурного поля плоского сечения ограждающей конструкции любой конфигурации с различным сочетанием строительных материалов (металла, высокоэффективного утеплителя и др.), с разными значениями теплопроводности. Граничные условия и коэффициенты теплообмена могут быть заданы вдоль любой части границ рассматриваемого плоского сечения конструкции в следующих видах: в виде теплообмена между поверхностью конструкции и внутренним или наружным возду-i хом с определенной температурой и при известном значении коэффициента теплообмена; в виде теплообмена между поверхностью и замкнутым воздушным пространством с нулевой плотностью теплового потока или в одной и той же среде по поверхности, представляющей плоскость симметрии конструкции (в этом случае формально следует принимать коэффициент теплообмена равным нулю); в виде постоянной температуры на поверхности или в любой части внутри конструкции (стояки системы отопления или другие виды источников тепла); в виде дополнительного теплообмена на пересечении поверхностей, образующих между собой прямые углы (например, угол между перегородкой и наружной стеной). . Для построения метода расчета стационарных дву
Мерных температурных полей воспользуемся основными принципами, изложенными в работе [48][7].
Рассмотрим некоторый условный фрагмент плоского сечения конструкции (рис. 34). Предположим, что по поверхностям этого фрагмента (т— 1, т+1), (т— 1, п—я), (i, i-j-l) происходит теплообмен с наружным и внутренним воздухом с температурами и коэффициентами теплообмена, указанными на схеме рис. 34. Поверхность (/+1, i-f-1) является осью симметрии, вдоль которой коэффициент теплообмена принят равным 0, т. е. передачи тепла в направлении оси х от этой поверхности нет. В угловой точке I происходит дополнительный теплообмен с внутренним воздухом, коэффициент теплообмена — ауг. На плоское сечение нанесена прямоугольная неравномерная сетка, элементарные прямоугольники которой имеют размеры Ахи Ах2, Ау, Ау2, Az/з. Материалы конструкции в пределах каждого элементарного прямоугольника имеют постоянную теплопроводность. Это значит, что горизонтальные и вертикальные линии прямоугольной сетки проходят в первую очередь по границам примыкания материалов с различными теплофизическими свойствами. Размеры Ах, Ау принимают такими, которые обеспечивают требуемую точность разностной схемы и расчетов. Таким образом, в данном фрагменте синтезирована общность поставленной задачи.
|
TH,DL. |
Известно, что процесс передачи тепла в данном фрагменте описывается системой линейных двумер
ных дифференциальных уравнений Лапласа при условии сопряжения по контуру элементарных прямоугольников и с соответствующими граничными условиями. Для расчета температур в наиболее характерных точках фрагмента I—1, I, i+1, /—1 получаем следующую систему алгебраических уравнений [48, с. 61, и формулы (15)-(18)]:
Tn_! - i-1 - АН (Ah "I" A-V3) + kU-1 +
+ V-1. 1 + ku-1 h + ki-1, i-1 '/-1 =
= — ан (Аг/з + Ду3) ^я!
*«.< + ^-i. i U-i ~ [bN. i + kt-1.,+ ki+ut + khi +
+ АУг (Л*2 + U + kt+l. t *t+l + ki, i *] =
= ~'ayr (Лх2+Л^з) (18>
Ku+l U - (ki, i+1 + АВ Лх2 + k/+Wi+l) fi+1 + + kj+U+i
/_! - y_i + ан (Д^ + + kul_x +
+ k, n-, /—l] + k!,i-1 ^ + ^m-1, /-1 ^m—1 = = — <*H (Д'/l + Д^2) ^H i где величины & определяют в соответствии с системой (18), приведенной в работе [48]. Если коэффициенты при неизвестных температурах
Tn—, tn, t{_i, t., ti+1, t., tj+i, tm_i
Обозначить через а с соответствующими индексами, то матрица данной системы алгебраических уравнений будет иметь вид
J—I А, ,
|
X |
|
(19) |
А.
At+l. t ai, t+1 АЖ. i+1
Fl/+i. ж 0
Am—1,/—1
О
Очевидно, число столбцов данной матрицы равно числу определяемых температур и при расчете темпе-
Ратурного поля в обычных плоских сечспиях конструкций решение соответствующей системы алгебра][ческих уравнений чрезвычайно сложно даже при возможностях современных ЭВМ. Однако анализ матрицы (19) при ее дальнейшем расширении показывает, что число ненулевых элементов значительно меньше и они сосредоточены в некоторой диагональной полосе, осевую линию которой составляют элементы й, а.,а
Очевидно, число этих элементов равно числу определяемых температур, т. е. числу расчетных узлов по сечению конструкции Поэтому матрицу (19) можно переписать в виде
Где справа также приведена матрица, предстазляющая собой столбец значений правых частей системы уравнений (18).
Отметим некоторые особенности матрицы (20), облегчающие ее формирование и решение системы (18) методом исключения. Каждая строка матрицы (20) или уравнение системы (18) соответствует неизвестной величине (температуре), коэффициент при которой располагается в середине строки [по центральному столбцу матрицы (20)]. Слева и справа от центрального столбца расположены столбцы, содержащие соответственно коэффициенты при неизвестных температурах узловых точек, находящихся слева и справа от данной рассматриваемой узловой точки (см. рис. 34). Далее на каждой строке матрицы на некотором удалении влево и вправо от центрального столбца расположены элементы, соответствующие коэффициентам при неизвестных температурах узловых точек на верхней и нижней горизонтальных линиях по отношению к рассматриваемой узловой точке. Например, для узловой точки J такими узловыми точками являются I и т (см. рпс. 34). Удаленность этих точек от центрального столбца соответствует количеству узловых точек между рассматриваемыми при порядковом их отечете. Например, уда- ленносГь точки п—1 От центральной точки /—1 составляет число точек: п—1, п, т. е. две; а удаленность точки т от / составляет: т, т—1, /+1 точек, т. е. три. Следовательно, ширина матрицы (20) определяется величиной 2М--, где М — максимальная удаленность двух соседних по вертикальной линии узловых точек по всему данному плоскому сечению ограждающей конструкции. Размерность матрицы (20), очевидно, равна (2М-{-) N, Где N — общее число узловых точек, температуры в которых необходимо рассчитывать.
В матрице (20) элементы центрального столбца всегда отличны от нуля. Остальные элементы могут быть и нулевыми, что указывает на отсутствие соответствующих узловых точек на плоском сечении конструкции (например, при расположении основной расчетной точки на поверхности конструкции). Поэтому систему алгебраических уравнений (18) можно решить методом исключения по главным элементам следующим образом.
В матрице (20) рассматривают первые М-- строки и сдвигают влево элементы первой строки на М позиций, второй — на М—1 позицию и т. д. вплоть до последней, которая уже не подвергается сдвигу. В полученной системе исключают неизвестные до порядка М путем деления левых и правых частей системы уравнений (18) на главный элемент. Дальнейшее исключение неизвестных порядка выше т продолжается с последовательным присоединением к полученной последней строке (с предварительным сдвигом ее влево на одну позицию) остальных строк матрицы. Значения температур в узлах получают обратным ходом.
Таким образом, алгоритм описанного метода исключения довольно прост, легко реализуется и распространен при программировании систем алгебраических уравнений с матрицей ленточной структуры. Погрешность метода, складывающаяся из накопления ошибок округления, в данном случае, как показали специальные расчеты, невелика, а эффективность и скорость выполнения расчетов на ЭВМ вполне отвечают практическим требованиям.
Описанный метод расчета двумерных температурных полей с помощью ЭВМ сам по себе достаточно прост. Однако организация счета коэффициентов теплопередачи K в уравнениях (18), формирование основной матрицы и матрицы правых частей требуют в постановке задачи, в подготовке исходных данных и в программировании поиска и разработки наиболее рационального подхода. Возникающие на этом пути сложности являются следствием универсальности постановки задачи, необходимости учесть произвольность конфигурации сечения конструкции, воздействий тепловых источников, условий дополнительного теплообмена в углах конструкции и др. Приведенная в приложении программа на ЭВМ предназначена для практических расчетов двумерных стационарных температурных полей узлов ограждающих конструкций. На этой программе проиллюстрированы все приемы и методы реализации описанного выше алгоритма.
Оценка теплотехнического режима конструкций легких стеновых панелей (см. ниже) проведена на основе расчетов двумерных температурных полей по данной методике (по вычислительной программе на ЭВМ М-222). Все необходимые для расчетов теплотехнические показатели и характеристики теплообмена конструкций с внешней средой выбраны в соответствии с данными проектных документов, а также руководств [29, 35, 36, 45].
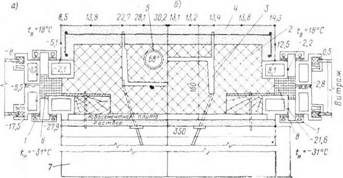
В качестве примера рассмотрим прежде всего наиболее часто встречающиеся конструкции примыканий витражей с металлическими элементами к наружной стеновой панели в эксплуатируемом здании библиотеки АН СССР (по Профсоюзной ул.). На рис. 35 показаны конструктивные решения данного узла: со стояком отопления в панели и с гернитовым шнуром между стальными профилями витражей (а), без стояка отопления, с утеплением стальных элементов витражей пенополи - стиролом (б). Фрагмент конструкции на рис. 35, а с методической точки зрения представляет собой наиболее общий случай для применения методики и программы расчета двумерных температурных полей. Поэтому этот фрагмент взят в качестве примера иллюстрации, и для него приведены расчетная сетка, подробный порядок подготовки исходных данных и расчет температурного поля с выдачей его в табличной форме (см. приложение).
Как показывает рис. 35, а, стояк отопления существенно не влияет на температурный режим элементов витражей, так как он утеплен значительным слоем ми-
|
Рис. 35. Температурное поле узлов примыкания витражей к наружным стенам в здании библиотеки АН СССР |
1 — металлические элементы витражей; 2 — минераловатиая плита, укладываемая в процессе строительства, 7=150 кг/м3; 3— швеллер № 14; 4— цементно - песчаная штукатурка по металлической сетке; 5 — стояк отопления (средняя температура воды 68° С); 6 — гернитовый шнур; 7 — пилон из известняка; 8 — Пенополистнрол, 7=30 кг/м3
|
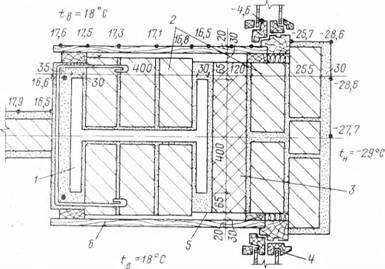
Рис. 36. Температурное поле несущей колонны с металлическими включениями в здании гостиницы на Университетском проспекте |
/ — металлическая колонна; 2 — кирпичная кладка, 7=1800 кг/м3; 3 — пеностекло, 7 = 400 кг/м3; 4 — оконный переплет; 5 — воздушная прослойка; 6 — древесноволокнистая плита, 7 = 600 1*г/м3
Нераловатной плиты. Большее значение имеет утепление стальных профилей витражей: в случае укладки герни - тового шнура температура на внутренней поверхности примыкания стальных профилей к стеновой панели равна минус 2,1° С, а в случае укладки пенополистирола (рис. 35,6) —плюс 8,1° С (более подробное температурное поле узла а приведено в приложении). Тем не менее указанные температуры поверхностей ниже температуры «точки росы» внутреннего воздуха и состояние внутренних поверхностей витражей в холодное зимнее время может оказаться неудовлетворительным. Во из< бежание образования конденсата на внутренних поверхностях металлических профилей необходимо дополнительное обогревание витражей горячим воздухом, что приведет, безусловно, к перерасходу тепла по витражам, но позволит создать в помещении требуемые са - нитарно-технические условия.
Другое температурное поле узла сопряжения наружной стены со стальной колонной (в здании гостиницы на Университетском просп.) показано на рис. 36. Результаты расчетов свидетельствуют о том, что температурный режим этого узла вполне удовлетворяет нормативным санитарно-гигиеническим требованиям. Минимальная температура на внутренней поверхности колонны равна 9,4° С, что превышает температуру «точки росы» (тр = 8,8° С при ф = 55% и TB= 18° С).
Ниже рассматриваются теплотехнические характеристики наружных ограждений с металлическими и другими теплопроводными включениями. Характеристики получены путем расчетов температурных полей на ЭВМ, а также на основании экспериментальных исследований.