Расчет длительности пребывания при температуре выше заданной
Длительность пребывания металла при температуре выше заданной ^зад выражается отрезком /н = *2 “ h на Рис - 7.1. Для определения /н необходимо, используя математическое выражение термического цикла ДО, вычислить корни t и О уравнения
Д0~Дад = 0. (7.13)
Рассмотрим два сварочных процесса: 1) наплавку на массивное тело и 2) однопроходную сварку листов встык, которые соответствуют расчетным схемам точечного источника на поверхности массивного тела и плоского источника в бесконечной пластине. Математические преобразования выполним для обеих схем, применяя модели быстродвижущихся источников теплоты и не учитывая теплоотдачи с поверхности (Ъ = 0). Используем выражения (6.37) и (6.41) для расчета термических циклов ДО, а также выражения
(7.3) и (7.4) для расчета максимальных температур Тт:
1) в случае трехмерного температурного поля при наплавке на массивное тело
/ (
|
(7.14) |
«w ч ^ Q/V г
|
т (r)-T =-^-v - • 1 mr f 1 h 2 ’ necpr |
|
(7.15) |
|
2) в случае двумерного температурного поля при однопроходной сварке листов |
|
Т(у, t)-T„= f - фл/ 4nat |
|
(7.16) |
|
ехр |
|
4at |
|
2 / / qlv I ne_____ 28cpy |
|
тт(у)-тн = |
|
(7.17) |
|
Разделив выражение (7.14) на (7.15), a (7.16) на (7.17), получим: |
|
‘Н _ |
|
1~ |
|
(7.18) |
|
ехр |
|
Tm-TH 4 at |
|
4 at |
|
Т-Т |
|
(7.19) |
|
ехр |
|
у] 4 at |
|
4 at |
|
З 2 Используя подстановку т =4at! г для выражения (7.18) и 2 т2 =4at/y для выражения (7.19), получим зависимости, которые Т-Т связывают безразмерную температуру 0 =---------------------- — с безразмерны ми параметрами времени т3 и т2: |
|
Т - Т Im ■'н |
|
]_ т3. 2_ *2 |
|
в(т3) = —■ехр х3 |
|
1- |
|
(7.20) (7.21) |
|
. уі2є е(т2) = -7=гЄХР 4х2 |
|
Уравнения кривых (7.20) и (7.21) описывают в безразмерных переменных термические циклы при нагреве тел быстродвижущи - мися источниками теплоты. Таким образом, все многообразие термических циклов для любых точек массивного тела или плас- |
|
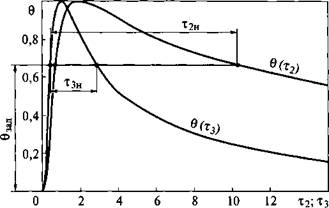
Рис. 7.3. Термические циклы в безразмерных переменных для схем нагрева массивного тела быстродвижущимся точечным источником 0(тз) И пластины быстродвижущимся линейным ИСТОЧНИКОМ 0(l2) |
тины при различных параметрах режима и разных теплофизических свойствах материалов выражается одной обобщающей кривой: 0(тз) - для массивного тела; 6(12) - для пластины (рис. 7.3). Сложная зависимость между многими переменными процесса распространения теплоты значительно упрощается и сводится к простой зависимости между двумя рационально выбранными безразмерными величинами, каждая из которых представляет собой простое сочетание нескольких переменных процесса. Из зависимостей, представленных на рис. 7.3, следует, что заданной безразмерной температуре 0зад соответствуют безразмерные длительности пребывания материала при температуре выше нее (тзн для
массивного тела и Т2Н для пластины).
Зависимости размерной длительности нагрева tH найдем, используя ее связь с безразмерными параметрами времени тзн и Т2Н (см. выше - определения параметров тз и 12):
|
(7.22) |
2 2 _ г _ у
'Зн-Т3н4^; '2н-Т2н4?
Расстояния г и у в (7.22) выражаем через максимальные температуры термического цикла, используя (7.15) и (7.17):
|
г2 = |
2 q/v
(7.23)
|
(7.24) |
|
У = |
v5
'її™ ср(Тт-Тн)
Подставляя выражения (7.23) и (7.24) в (7.22), окончательно получаем
/ =Т Г2 ^ТЗн 2 qlv
Зн Зн 4а 4алсф(гт-гн)
|
(7.25) |
т3н 2 qlv к 2 q/v.
4леЦ7и-Гн) 1ЦТт-Т„)'
|
ґ 2 ч_ vb |
|
JL у5 |
|
(7.26) |
|
Т - Т m 1н |
|
Т - Т m |
|
/ - т у - Т2н *2н - х2н~Г~~Г' 4а 4 а |
|
_ т2н 8 |
|
64 ле А. ср |
|
І2пе cp(Tm Гн) л2 = к2 |
|
Хер |
|
1 |
Входящие в выражения (7.25) и (7.26) коэффициенты кх = —^2-
4ле
х^
|
кї, к2 1,0 0,8 0,6 0,4 0,2 0 |
и к2= —— определяем по номограмме (рис. 7.4) в зависимости 64 пе
|
«і; к2 |
||
|
0,20 |
К |
|
|
0,15 |
- |
|
|
/кх |
||
|
0,10 |
V |
|
|
0,05 |
||
|
. J. - . J, . J______________ L. _L. _L _1________________ . |
0 |
I, . —— |
|
0,10 0,15 0,20 0,25 0 0,4 0,6 0,8 0 а б Рис. 7.4. Номограмма для определения коэффициентов к и к2 в зависимости от значений 0: 0,1... 0,3 (а) и 0,3... 1 (б) |
т - т
от безразмерной температуры 0 = -^-------------- —,------ где Тт - максималь-
Тщ ~ Тп
ная температура термического цикла в рассматриваемой точке изделия; Гзад - температура, длительность пребывания выше которой подлежит определению; Тн - начальная температура изделия.
Пример 7.4. Определить длительность пребывания при температурах выше 1000 °С точек околошовной зоны, лежащих вблизи зоны сплавления и испытавших нагрев до подсолидусных температур Тт = 1350 °С при электрошлаковой сварке стальных плит толщиной 6 = 800 мм. Эффективная мощность источника теплоты q = 130 кВт; скорость сварки v = 0,3 м/ч = 0,0083 см/с; начальная температура изделия Тн = 20 °С. Теплофизические коэффициенты: X = 0,40 Вт/(см • К); ср = 5 Дж/(см3 • К).
Решение. Поскольку при электрошлаковой сварке источник теплоты (шлаковую ванну) нельзя считать быстродвижущимся, то возможна лишь ориентировочная оценка. Применим схему линейного источника теплоты в пластине. Определяем безразмерную температуру:
|
0 = - |
Л _]000 - 20 = 0|73
Г.-Г. 1350-20
По номограмме (см. рис. 7.4) определяем значение коэффициента /:2 Для 0 = 0,73: *2 = 0,012.
Для определения длительности пребывания металла при температурах выше заданной используем выражение (7.26):
|
130000 0,0083-80 1350-20 |
|
_Я_ у6 |
|
= 1040 с * 17,3 мин. |
|
= 0,012 |
|
ha |
|
Хер |
|
Т - Т |
|
0,4-5 |