СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ СТЫКОВАНИЯ КРУГОВЫХ ЦИЛИНДРИЧЕСКИХ ТРУБ
Теоретическое решение
Рассмотрим случай стыкования длинных тонких стальных труб кругового поперечного сечения одинаковой толщины б и одинакового радиуса срединной поверхности R. Поместим начало координат в точке срединной поверхности на оси шва, направив ось х вдоль образующей трубы, а ось z — внутрь от срединной поверхности.
Обозначим через ± b, расстояние от оси шва до огибающих подвижной изотермы Тк предельного состояния нагрева, через ±Ь2— расстояние от той же оси до огибающих подвижной изотермы Ту, определяющей границы пластических деформаций нагрева в том же предельном состоянии. В соответствии с основной гипотезой вся область составной трубы, ограниченная сечениями
Ьл 4" b о і о
х = ± — 2 - — ± о, при прохождении электрода по замкнутой
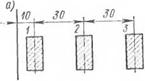
окружности получит активную пластическую деформацию сжатия а (Тк — Т0) в направлении перемещения источника. Другими словами, если каждый элемент, находящийся внутри этой области, освободить от остальных частей составной трубы в момент Т = Тк, то в результате прохождения электрода по замкнутой окружности и последующего остывания получим короткую трубу 1 длиной 2b и радиусом Rі = R [1 — а (Тк — Тр) ] и две длинные трубы 2. Толщина длинных труб 2 будет постоянна и равна 62 = б, а труба 1 будет иметь переменную по длине толщину, среднее значение которой обозначим через бх. При этих условиях задача определения приближенных значений сварочных деформаций (напряжений), возникающих в результате стыкования исходных труб, сведется к определению деформаций (напряжений) составной трубы, получающейся путем сшивания трубы 1 с длинными трубами 2.
В силу симметрии относительно плоскости х — 0 условия сшивания можем написать в виде:
| ш<‘> (Ъ) | + иКЧ (Ь) = Ra (Тк - Т0);
|
dwС*> |
dwВ) dx
|
(8.96) |
dx
м™(Ь) = м™(ьу,
Qi" (b) = q[2) (b).
Рассмотрим сначала упругое состояние составной оболочки. В этом случае прогибы к>(1) (х) и ьу(2) (х) в отдельных частях
составной трубы будут удовлетворять дифференциальному уравнению [120]
|
(8.97) |
|
dx* |
Р'У0 = 0,
где
|
Р? |
3(1 — и2)
2с2
>т
В силу симметрии относительно плоскости А = 0 к,,(|) (а) будет четной функцией от х:
ww (х) = CSX) ch [Зі*cos PiX - f СгХ> sh Pi* sin pi*. (8.98)
Аналогично для правой длинной трубы 2 будем иметь
W(2) (X) = е~ргХ (Cp cos р2А- + CP sin Р2а). (8.99)
Для определения постоянных интегрирования Сі1*, Ср, СР, Сг2)используем условия сшивания (8.96), которые, если иметь в виду соотношения:
|
(8.100) |
|
dsw dx3 |
Q(x) = —D
где
|
(8.101) |
Ed3
D.
12(1 — p2) ’
дадут следующую систему алгебраических уравнений: C^cosr]! сііці— С^1) sin T)x sh + (Cj2) cosT]2 + Cp sin Г]2)е~Чг = Ra {TK — T0);
Pi [Ci1} (cos hi sh t)i — sin i]i ch rjt) -f - - f CP (cos hi sh r)i - j - sin rji ch ці)] =
|
(8.102) |
= —p2 [Cp (cos T]2 + sin T)2)— Cp (cos r]2 — Sin 1]2)] e ^ 2Dipi (СІ1* sin r|i sh ці — CP cos hi ch hi) =
= —2DzP2 (Ci2) Sin Ц2 — CP cos - Hz) e p 2D$i [CiX) (cos Ці sh ці + sin ці ch ці) —
— CP (cos ці sh ці — sin Ці ch Ці)] =
=—2DzPl [CP (cos ц2—sin r)2)+CP (cos Цг+sin ц2)] 3
|
(8.103) |
где
hi = PA ha = Рг^-
|
Решением этой системы будет: £(1) _ _ Rg (Тк — То) ch ‘Mi cos тп |
|
+ |
|
ch2 г)! cos2 rj! + sh2 rj, sin2 ти 6- 2 |
|
j^ch % cos Hi cost]2 — (75^) stl 111 sin 111 sin ’1a] e ch2 in cos2 i]t ■{ sh2 in sin2 in j^ch TJj COS in sin Г)2 + s'n T'1 C0S ^2 j ch2 rn cos2 in + sh2 іц sin2 Пі £(i) __ _ Ra (TK — ^shrit sin rit, ch2 Hi cos2 rjx + sh2 in sin2 in ^sh in sin in cos t)2 + ch % cos % sin rj2 j < ch2 r]x cos2 in - h sh2 T]t sin2 in j^sh rjj sin rjt sin T)2 — C0STli cosr)2 j |
|
П2 |
|
(2) |
|
+C[ |
|
+ |
|
„-lb |
|
+ CP |
|
-Пи |
|
+ Cf>- + ci2) |
|
+ |
|
, Vl |
|
(21 ^ ^Tk c — |
- T0) ё*‘ |
к |
ж |
(-%) “s'fc |
] |
|
( +*(*: |
ЖI M |
>(*) ып |
*] = + ]-Ш |
V2 a |
|
ch2 Ці cos2 i]j + sh2 Пі sin2 i]i |
|
+ |
|
(8.104) |
|
Re^2a.{TK — T0) /2 d ^a(cosT)2— sin T)2)
|
|
+ |
|
Re"‘a(TK-T0) |
И |
’ 2 / Sj d j |
1 sin ТІ2 |
|
mh [ ЖЖ1Ж |
і + 9 < |
(№ зм+’і |
ЖГ‘ |
|
Re^a (TK — T0) /2 d [“ (cos i]2 + sin r]2) — |
|
с?1 |
|
+ |
|
~ 2 “(cosin — sin тп)!] (j_)V(57] i+ |
|
+ |
а = ch ті j sh г] г — sin ц t cos ;
a = ch T] t sh r) x 4- sin rj 1 cos tj x; d = ch2 r] j cos2 r] j sh2rj xsi n2 rjj; d! = ch2 t] і sh2 T] x + sin2 cos2 rjj
и принято Rx ^ R.
|
т°с |
|
|
В каждом конкретном случае, подсчитав численные значения постоянных интегрирования, по формулам (8.98)—(8.100) можно определить прогибы, изгибающие моменты и перерезывающие силы в отдельных частях составной трубы, находящейся в упругом состоянии. Но в зависимости от величины основного параметра а (Тк — Т0) составная труба после сшивания может оказаться в упруго-пластическом деформированном состоянии. Впервые пластические деформации возникнут j ч в тех точках составной трубы, где интенсив
ность деформаций
достигнет значения е1ь. Интенсивность деформаций является четной функцией z и для любого х по толщине трубы изменяется от своего минимального значения
|
®I mln |
|
на срединной поверхности 30 г, мм д0 своего максимального значения |
(8.106)
'—-ЙУтШ'+т, (-£-)' (fU07>
на поверхности трубы при z — ± —.
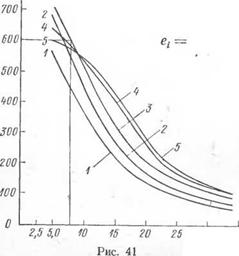
Рассмотрим численные значения et для стальных труб, использованных для опыта. Проведенное исследование показало, что предел текучести металла трубы в исходном состоянии os = = 2400 кПсм2. Радиус срединной поверхности трубы R = 18, 35 см, толщина стенки (см. п.41) 6 = 62 = 0,5 см. На рис. 41 приведены температурные кривые 1—5, соответствующие отсчетам 7—10. Как показали замеры температуры в процессе сварки, в данном случае b «=* 2,0 см. Подсчеты показали, что средняя тол
щина трубы 1 с учетом наплавленного металла 6j = 0,57 см. Принимая для стали Е = 2 • 106 кГ/сма, р, = 0,3, по формулам (8.104) для постоянных интегрирования получим:
С}1^ —0,207Ясс(Тк —Т„);
|
С{2 с[2). |
|
(8.108) |
’"-(1) ~ • — 0,296/?а (Тк — Т0);
^,305Re^a(TK — Toy,
> 0,565Rev‘cc (Тк — Т0);
При этом для минимальных и максимальных значений ег в сечениях х = 0, х — ±Ь труб 1 и 2, используя выражения (8.98),
(8.99) , по формулам (8.106) и (8.107) будем иметь:
SHAPE * MERGEFORMAT

|
е*4-' w min е(1) Єї max Єї min e{1) Єї ша е(2) ■ Єї min е(-2) Єї та |
|
(8.109) |
(0) ~ 0,207а (Тк — Т0); (0)0,602а (Тк — То); (Ь) 0,389а (Тк — Т0);
х (6)^ 0,481а (Тк — То);
(6) л, 0,614а (Тк — Т„); х (6)*«0,717а (Тк - То).
Отсюда ясно, что при сшивании труб 1 и 2 пластические деформации впервые появятся в точках х = ±b, z = ± —труб2при
том значении основного параметра а (Тк—Т0), которое определится из условия
. (Ь) = 0,717а (Тк - То) = 0,717аТк,
6is — max
что при еи = - д-(1 + Iі) eso [1171, а = 12,5-10 6 eso = 0,2%
дает Тк = 193° С.
При последующем увеличении основного параметра пластические деформации будут распространяться во внутренние точки сечения х = Ь трубы 2. Для простоты приближенно можем принять, что пластические деформации во всех точках сечения х — b трубы 2 возникают одновременно при том значении основного параметра, при котором m,-n (b) достигает величины els. Соответствующее значение этого параметра найдется из равенства
С/ min (^) = Cis,
которое дает Тк = 225° С.
Здесь рассматриваем малые деформации труб 2, металл которых, имея площадку текучести, в пределах малых деформаций следует схеме идеальной текучести. Поэтому с известным основанием можно принять, что при значении Тк = 225° С основного
параметра в сечениях х = ±b составной трубы появляются пластические шарниры и при последующем увеличении основного параметра до его нормального значения а (Тк — Т0) деформации, изгибающие моменты и перерезывающие силы во всех сечениях составной трубы, кроме сечений х — ±Ь труб 2, останутся неизменными. Другими словами, прогибы, изгибающие моменты и перерезывающие силы в отдельных сечениях составной трубы после сшивания приближенно определятся по формулам (8.98)—
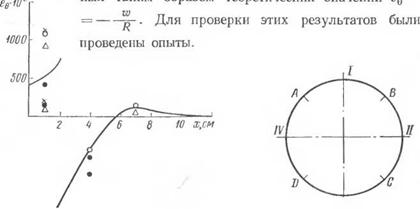
(8.100) , если в выражения коэффициентов (8.98) вместо Тк— Т0 подставить Тк = 225° С. На рис. 42 приведена кривая получен-
...п ных таким пбпяапм теппртичрских янянрний —
|
|
|
0 |
|
о |
|
ш Рис. 43 |
|
Рис. 42 |
Опытная проверка [7]
Для опытов были использованы заготовки — две трубы малоуглеродистой стали, каждая из которых имела длину I = 500 мм, толщину 11 мм, наружный диаметр 378 мм, внутренний диаметр 356 мм.
Эти трубы протачивались изнутри и снаружи на одинаковую глубину на токарном станке до остаточной толщины стенки б — = б2 = 5 мм. Таким образом, радиус срединной поверхности каждой из подготовленных к стыкованию труб был равен R = = 183,5 мм. Торцовые сечения этих труб были разделены на четыре одинаковых участка (рис. 43) и их стыкование производилось по участкам в следующей последовательности: сначала заваривался участок от Л до Б (рис. 43), затем — от С до D, от Б до С и, наконец, отD до А. Температура в процессе сварки измерялась путем одновременных отсчетов по восьми гальванометрам, к которым были подключены термопары, прикрепленные к образцу. Первая термопара была установлена на расстоянии 2,5 мм от
кромки трубы, вторая — на расстоянии 5 мм от кромки и все последующие через каждые 5 мм. На рис. 41 приведены температурные кривые нагрева и остывания, построенные по данным отсчетов 7, 8, 9, 10, 11. Кривая отсчета 9 может быть принята за температурную кривую предельного состояния нагрева. Для металла трубы as = 2400 кПсм2, Тк = 600е С, в силу чего по кривой отсчета 9 получим f>i = 7,8 мм, Ь2 = 32,5 мм и, следовательно, b — 20 мм.
|
|
Для замера деформации были использованы проволочные датчики сопротивления, которые приклеивались к поверхности трубы после сварки и полного остывания изнутри и снаружи друг против друга вдоль четырех симметрично расположенных обра-
|
5) /Г-ЧЪ-Та)
|
зующих /, II, III, IV (рис. 43) в соответствии со схемой на рис. 44, а. Датчики с внутренней стороны имеют номера 2', 3'. После сушки и стабилизации показаний по всем этим датчикам были сняты начальные замеры, а затем каждая пара датчиков вырезалась из трубы и по ним снимались последующие замеры. Датчики 1, V, 3, 3'(1); /, 2'{II); Г, 2, 2', 3, З'(Ш); /, 2, ґ(IV) не дали показаний после вырезки из-за повреждения при вырезке.
Опытные значения ев показаны на рис. 42 по сечениям; / — • II— О; III— X; IV— Д. Сравнение опытных и теоретических значений ев указывает на их удовлетворительное соответствие, причем результаты, приведенные в этом параграфе, подтверждают то, что было установлено опытным путем другими авторами [93].
Сварочные деформации и напряжения, возникающие в результате стыкования толстостенных труб, могут быть найдены или методом сшивания, использованным выше, или методом мгновенного охлаждения зоны активных пластических деформаций нагрева, при котором в простейшем случае задача сводится к определению деформаций и напряжений длинной толстостенной трубы в результате мгновенного охлаждения до 7’. = —(Тк — Т0) ее средней части (рис. 44,6).
Упругие тепловые напряжения вблизи сварного соединения разнородных труб рассмотрены в работе [16]. В ней анализированы только упругие деформации при нагреве, обусловленные различием коэффициентов теплового расширения. Возникновение
пластических деформаций при нагреве и влияние на них различия в параметрах Тк металлов этих труб не рассматривается. Тем не менее в этой работе схвачена основная черта этого класса задач — разрыва в соответствующих составляющих тензоров напряжения и деформаций.
В работе [90] дано исследование деформаций тонкой цилиндрической оболочки от сварки кольцевого шва. Эти работы базируются на теории Н. О. Окерблома [83, 85, 86]. Для определения пластических деформаций нагрева используется гипотеза плоских сечений без какого-либо обоснования. Кроме того, как и в теории Н. О. Окерблома, автор работы [90] не учитывает, что пластическая деформация нагрева, соответствующая а (Т — Тк) при Т > Тк, не оказывает влияния на остаточные сварочные деформации и напряжения (п.28). Автор не дает сравнения своих теоретических результатов с опытными данными.
Изложенные в этом параграфе результаты относятся к стальным трубам. При сварке труб из алюминиевых сплавов, имеющих значительно больший коэффициент теплопроводности, чем сталь, большое влияние на пластическую деформацию зоны нагрева, где Т 5= Тк, может оказать температурное расширение всей остальной зоны, где Т <<ТК (см. стр. 149 в работе [201).