СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ С ПРИМЕНЕНИЕМ ПЛАСТМАСС
Расчет трехслойных оболочек
Расчет трехслойных оболочек, имеющих несомненные перспективы применения в строительных конструкциях, представляет актуальную задачу строительной механики. Элементы оболочек, как и трехслойные панели, могут иметь по контуру ребра или быть чисто трехслойными.
Анализируя исследования по расчету трехслойных оболочек, проведенные применительно к авиации, можно отметить, что они в большей части посвящены расчетам конструкций, представляющих малый интерес для строительства: например, круговому цилиндру, коническим, сферическим оболочкам, цилиндрическим оболочкам, опертым по контуру. Между тем в строительстве находят основное применение цилиндрические оболочки, опирающиеся на криволинейные края или на три стороны (у оболочек, расположенных в торцах здания).
С целью определения влияния деформаций сдвига на деформиро - ванно-напряженное состояние цилиндрической трехслойной оболочки в ЦНИИСК был разработан точный метод расчета с учетом деформаций сдвига по среднему слою [112].
В основу этого метода положены следующие предпосылки (гипотеза Рабиновича-—Райснера):
1) модуль упругости среднего слоя в направлении срединной поверхности оболочки равен 0, продольные усилия и моменты воспринимаются только обшивками;
2) поперечные силы воспринимаются средним слоем, который также передает нормальные силы в направлении, нормальном к срединной поверхности;
3) средний слой рассматривается как упругий материал;
4) нормальные напряжения распределяются равномерно по толщине обшивок.
Вывод уравнений равновесия для трехслойных цилиндрических оболочек был сделан по схеме Райе - нера [91]; для решения полученной системы из пяти дифференциальных уравнений в частных производных, в вычислительном секторе ЦНИИСК составлена стандартная программа.
Точный метод расчета трехслойных цилиндрических оболочек очень трудоемок и требует участия электронной счетно-вычислительной машины. Имея в виду, что влияние деформаций сдвига при наличии жестких ребер из бакелизированной фанеры вдоль ската оболочки с шагом 1,5 м (рис. 1.33) должно быть незначительным, был применен для расчета оболочек метод перемещений, разработанный И. Е. Милейковским применительно к однослойным оболочкам и проверенный на оболочках из железобетона [70]. В расчет помимо общих предпосылок, принятых для однослойных оболочек, были введены следующие дополнительные допущения, учитывающие характер распределения усилий в трехслойной конструкции:
1) нормальные усилия NI и N2F нормальные напряжения от поперечных изгибающих моментов М, сдвигающие усилия 5 (рис. 5.25) воспринимаются обшивками;
2) поперечные силы Q воспринимаются средним слоем (в натурной конструкции — ребрами, а при отсутствии ребер — пенопластом);
3) средний слой обеспечивает устойчивость сжатой обшивки и восприятие местной нагрузки.
В зависимости от соотношения длины 1 и ширины /2 цилиндрические оболочки разделяются на три группы: длинные /i//2>3, средние
1 3 и короткие L/l2 < 1.
2
|
|
|
Г ': 1 Рис. 5.25. Схема цилиндрической оболочки А — общий вид; б — поперечное сечение |
Расчет длинных и средних трехслойных цилиндрических оболочек представляет наибольший практический интерес.
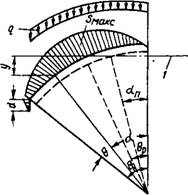
Расчет длинной оболочки. На основании опыта теоретических и экспериментальных исследований тонкостенных и пространственных конструкций, в основном железобетонных [47], было установлено, что длинная цилиндрическая оболочка или призматическая складка, имеющая открытое симметричное сечение со свободно висящими продольными краями, при симметричной нагрузке деформируется в продольном направлении, как балка с жестким поперечным контуром; продольные перемещения по высоте поперечного сечения распределяются в соответствии с гипотезой плоских сечений. При расчете определяются нормальные усилия в пЬперечных и продольных сечениях оболочки N± и N2 (см. рис. 5.23), сдвигающие усилия 5, поперечные изгибающие моменты М и соответствующие им поперечные усилия Q. Изгибом поперечного контура, в соответствии с изложенным, пренебрегают.
|
Рис. 5.26. Эпюра сдвигающих усилий в поперечном сечении цилиндрической оболочки |
|
J — нейтральная ось |
_ Для определения продольных нормальных напряжений в обшивках а2 и вертикальных прогибов VB можно использовать обычные формулы сопротивления материалов, которые для равномерно распределенной нагрузки имеют вид:
GR В1 i
У кГ/см2;
10 qR^n
VB = — . —=------------------------------ CM,
В 384 Е J
Где q—вертикальная равномерно распределенная по поверхности нагрузка в кГ/см2;
R—радиус срединной поверхности оболочки в см;
0! — половина центрального угла поперечного сечения оболочки (по срединной поверхности);
1г— пролет оболочки в см
Е— модуль упругости материала обшивок в кГ]см2
J—момент инерции сечения оболочки относительно нейтральной оси; положение нейтральной оси и момент инерции можно определить по формулам [99], принимая сечение оболочки однослойным с толщиной, равной толщине двух обшивок;
У—расстояние от рассматриваемого волокна сечения оболочки до нейтральной оси.
Положительное значение VB соответствует прогибу вниз, а положительное значение а2—растяжению.
Величины остальных усилий определяются из уравнений равновесия отдельных частей оболочки.
Сдвигающие усилия 5 можно определить из условия равновесия элемента оболочки Dx Ds относительно оси х (рис. 5.26):
S = Гi*. dF=8R Г ^dB КГ/См. (5.97)
J d* J dx
F e
Сдвигающие усилия по пролету изменяются пропорционально изменению поперечной силы от внешней нагрузки и достигают максимального значения на опорах (см. рис. 5.26). Исходя из допущения о восприятии сдвигающих усилий обшивками, легко найти величину касательных напряжений, действующих в обшивках вдоль осей х и S:
Rx, s=xs. x=^-Kr/cM (5.98)
Если найдена в общем виде зависимость продольных нормальных напряжений а2 в среднем поперечном сечении оболочки от угла (5.95), то после некоторых преобразований формулу (5.98) для обшивок можно записать в виде:
Тх.. «Т,.. (5"99)
1 е
Для бортового элемента *
Т= (5.100)
1 D
Сдвигающие усилия положительны, если направлены по касательной к контуру сечения в сторону его середины.
При использовании формул (5.95), (5.99), (5.100) для приближенного расчета длинных однопролетных оболочек следует иметь в виду, что расчет тем точнее, чем меньше высота сечения, так как усилия определяются относительно срединной поверхности. При вычислении момента инерции сечения и вертикального прогиба этой неточностью можно пренебречь. Но при вычислении максимальных нормальных напряжений в обшивках при относительно большом расстоянии между ними следует проверить ог2 при значениях у, соответствующих нижнему и верхнему крайним волокнам реального контура сечения.
Усилия, действующие в продольных сечениях оболочки и отличающие ее от балки корытообразного профиля, устанавливают из условия равновесия поперечной полосы единичной ширины под действием внешней нагрузки и сдвигающих усилий [70]. Каждая такая поперечная полоса находится в равновесии, так как внешняя нагрузка уравновешивается разностью сдвигающих усилий между соседними поперечными сечениями — приращением сдвигающих усилий AS на единицу длины оболочки. Так как при равномерно распределенной нагрузке изменение сдвигающих усилий S по пролету носит линейный характер, то их приращение на единицу длины можно определить следующим образом:
AS = J*»-КГ/см-см, (5.101)
1х! 2
Где S0— сдвигающее усилие в опорном сечении; /х/2—половина пролета оболочки.
Внешняя нагрузка Q и приращение сдвигающих усилий вызывают в поперечной полосе изгибающие моменты М, соответствующие им поперечные силы Q й нормальные силы NЗначения М, Q и N± можно найти, рассматривая поперечную полосу как криволинейную балку, нагруженную внешней равномерно распределенной вертикальной нагрузкой и действующими в срединной поверхности усилиями AS.
Для цилиндрической оболочки, не имеющей бортовых элементов, усилия от действия А5 выразятся следующим образом:
А ап
Мп = j" dMn = j AS/?2 [ 1 — cos {a — An) da; (5.102)
0i 0i
DM* dMsn i dMsn Qn --------- - - — • (5.103)
Ds Rda R da 4
A an
Na= j' ASR cos (a — an) da. (5.104)
01 01
Для определения M, Q и Nx от внешней равномерно распределенной по поверхности нагрузки можно использовать формулу [70]
Мп = QR2 (ап sin Ап + cos Ап — 8i sin Ап — cos 0!); (5.105)
= ЛИ* 1 = ^ _ ^ cQs ^ ^ Ш6)
Аа
N°in=qR (0i - оО sin Ап. (5.107)
После определения усилий, действующих в поперечном направлении, можно определить нормальные напряжения, зависящие от Мп = = М°п + Msn и Nl П = iVJ я + касательные напряжения, завися
Щие от Qn = + Q® .
Если при рассмотрении работы оболочки в продольном направлении можно было с известной степенью точности пренебречь расстоянием между обшивками и считать оболочку однослойной, то при расчете оболочки в поперечном направлении следует учитывать особенности расчета трехслойных конструкций (см. выше). Для определения нормальных напряжений можно пользоваться обычными формулами сопротивления материалов с учетом допущения, что нормальные напряжения воспринимаются обшивками, а касательные — средним слоем:
(5Л09)
Где М, Ni и Q определяются по формулам (5.102) — (5.107).
Расчет оболочка средней длины. Для расчета модели оболочки средней длины был принят метод перемещений [70]. В расчете применяются указанные ранее допущения, общие для длинных и средних оболочек, а также учитываются деформации изгиба поперечного контура. Допускается, что напряженное состояние такой оболочки характеризуется нормальными и сдвигающими усилиями Nu N2 5, изгибающими моментами М и поперечными силами Q.
Из рассмотрения деформаций системы определяются усилия N2 и моменты М. Остальные усилия определяются из условия равновесия элементов оболочки относительно соответствующих осей.
В [70] получена система алгебраических уравнений для однопролет - ной оболочки, выражающих условие равновесия поперечной полосы ши-
риней Dx в виде работы всех внешних и внутренних сил на возможных перемещениях:
• I (5Л10)
I
(j,i = О, 1,2,..., с),
Где а. £ — коэффициенты, учитывающие работу продольных усилий N2 И характеризующие жесткость поперечного сечения оболочки на растяжение (сжатие);
SjЈ — коэффициенты, учитывающие работу поперечных моментов М и характеризующие жесткость поперечного контура оболочки на изгиб;
F? — неизвестные параметры, получившиеся при разложении функций перемещений в тригонометрические ряды и определяемые из системы (5.110);
<7/— свободные члены уравнений, представляющие собой интегральную сумму по сечению работ внешних вертикальных сил на единичные вертикальных перемещениях;
Для определения коэффициентов системы (5.110) можно воспользоваться формулами, приведенными в [70]. Следует, однако, помнить, что при определении коэффициентов, характеризующих жесткость поперечного контура, нельзя пренебрегать толщиной среднего слоя.
Для трехслойной оболочки
= & ®l-Yajh (5.111)
J б (с + б)2 „ „
Где «/= —*—5—------- момент инерции трехслойной полосы единичнои ширины;
Б — толщина обшивки; K — L/R — кривизна оболочки;
Из системы (5.110) определяются параметры функций перемещений, и при заданных в различных вариантах единичных функциях можно найти нормальные напряжения а2 и поперечные моменты Л1, а затем и другие искомые величины.
Особенности расчета светопрозрачных конструкций
Светопрозрачные конструкции разделяются на две основные группы (см. главу 1): 1) изготовляемые на основе светопрозрачных волнистых листов и 2) трехслойные с обшивками из плоских листов стеклопластика и средним слоем различного вида.
Формулы для статического расчета трехслойных светопрозрачных конструкций, относящихся к панелям типов I и И, описаны выше. Поэтому ниже указываются лишь некоторые особенности статического расчета светопрозрачных конструкций, связанные со спецификой их конструи-
Рования (закрепленные по контуру), а также данные по статическому расчету волнистых листов. Кроме того, приводятся данные по светотехническому расчету конструкций.
Особенности статического расчета светопрозрачных конструкций. Расчет конструкций из волнистых листов, при надлежащем их креплении на опорах, может производиться по формулам, принятым для балок
|
|
|
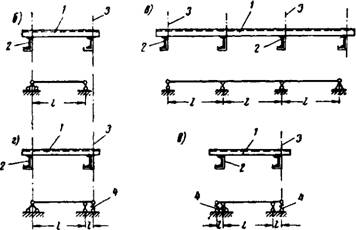
Рис. 5.27. Схемы для расчета волнистых листов А — сечение листа; б, в, г, д — возможные расчетные схемы: 1 — волнистый лист; 2—прогон; 3 — ось крепежного болта; 4 — податливая опора |
С недеформируемым контуром, т. е. по формулам сопротивления материалов.
Геометрические характеристики волнистых листов (рис. 5.27, а) на единицу ширины определяются по следующим формулам. Момент инерции
J = 0,035 /3 Н------------ (5.112)
В в BB sin А0 /
Момент сопротивления
(5.113)
HB+ о
Площадь поперечного сечения
F = 0,64 6 f 1 + 2Нв (5.114)
bB sin А0/
В формулах (5.113) —(5.114) ао вычисляется из условия
I 3,14йв
Tg«o= . »
Момент инерции /в, момент сопротивления WB и площадь поперечного сечения Fв одной волны могут быть определены также по табл. 31.
|
Таблица 31
|
Внутренние усилия и прогибы листов вычисляются по схеме балки, расчетный пролет которой равен расстоянию между прогонами или другими несущими конструкциями в свету (рис. 5.27,6 и в).
В случае опирания листа на стальные или железобетонные прогоны определение внутренних усилий и прогибов допускается производить с учетом упругой податливости крепления (см. рис. 5.27, г и (9). Податливость крепления при растяжении в см/кГ в расчете на один крепежный болт принимается равной:
Q-1.65 -/^ = 1,65 |/А.. (5.115)
|
Прочность волнистого листа проверяется по формулам: М _ мь W WB |
|
(5.117) (5.118) |
Гряется по формулам: <Яя; (5.116)
М __ MbB 1,92£бЛв
W Гв 4 + BlB 0,75 Q sin oc0 ^ D
Трехслойные светопрозрачные конструкции в ряде случаев имеют дополнительные закрепления на опорах, необходимые в связи с повышенной гибкостью конструкций из стеклопластика, имеющего низкий модуль упругости.
Расчет панелей с закрепленными опорными кромками может быть произведен с использованием работ [17, 103], в которых рассмотрены случаи шарнирного закрепления опор и закрепления с частичной заделкой.
Для поперечного изгиба панелей равномерно распределенной нагрузкой расчет производится по следующим формулам:
|
17* |
259
А) при шарнирном закреплении опорных кромок
/„("); (5-119)
' 384 Е J V V
Ммакс = Фо ("); (5.120)
О
Б) при частичной заделке опорных кромок вводится понятие о коэффициенте опорной пары г] = ( ) ' К0Т0РЬ1]"С 0ПРЕДЕляется отношением фактической величины изгибающего момента в опорных сечениях панели при данной степени их заделки M0TY к той величине момента, которая соответствует полной заделке обоих ее концов.
При этом
/ = ^ [5 (1 - г]) /о (и) + Nf (и)}; (5.121)
Ммакс = - ц) ф0 (и) + ЛФо («)]. (5.122)
Величины /о (и),Фо (и)> Fi(U) их (и) носят название параметров Буб-
/ 772
Нова и могут быть определены для значений и = —^ от 0 др 24 по
Рис. 5.28, а для значений и>2,4 по таблицам, приведенным в работе [17]. Параметр и, а следовательно, продольная растягивающая сила J и Т
Цепные напряжения а = — для случая шарнирного закрепления или ча-
Е
Стичной заделки кромок панели находятся по рис. 5.28 в зависимости от вспомогательного параметра
V=HVK~T' (5123)
Здесь
, _ 5Ql* /о —
384 Е J
F и J — площадь и момент инерции сечения панели;
/гм = --------------------- —коэффициент массивности опор.
^опоры + ^панели
Если соседние конструкции достаточно массивны, то кж =1. Однако для светопрозрачных панелей, опирающихся, как правило, на легкие конструкции покрытия, ku можно принять равным 0,5.
Расчет панелей с полной заделкой опорных кромок можно производить по обычным формулам сопротивления материалов, так как и в этом случае влияние продольных растягивающих усилий незначительно. Однако осуществление полной заделки, равно как и чисто шарнирного закрепления опорных кромок (см. рис. 5.29,а), конструктивно относительно сложно. Гораздо проще осуществляется частичная заделка опорных кромок путем выпуска за торец панели части верхней или нижней обшивки (рис. 5.29, б ив). При этом кроме реактивной продольной силы Т возникает опорный момент, который в зависимости от направления уменьшает или увеличивает прогиб, и напряжения в пролете панели. Если сечение
Панели симметрично относительно нейтральной оси, то величина опорного момента при частичной заделке приближенно определяется по формуле
+ (5.124)
М0.у = + Т-
Знак ( + ) относится к случаю верхней частичной заделки, знак (—) к случаю нижней частичной заделки.
Таблица 32
|
Минимальные значения первоначального коэффициента светопропускания Тх одного листа стеклопластика, применяемого при изготовлении панелей
|
|
Рис. §.28. График для определения параметров Бубнова |
|
V W |
|
V О? |
|
If |
|
V Ф V |
|
V |
|
Гр и |
Светотехнический расчет конструкций [53]. Один из основных факторов, определяющих конструктивное решение светопрозрачной ребристой панели из стеклопластика,— стью максимального свето - пропускания панели.
Для достижения минимально требуемой свето-
Прозрачности, не уступаю - w/s/A ' v//w.
Щей показателям традиционных конструкций для светопрозрачных ограждений, следует применять стеклопластики, удовлетворяющие требованиям табл. 32.
|
-it- |
|
Рис. 5.29. Возможные схемы закрепления панелей на опорах и их расчетные схемы А — шарнирное закрепление; б — частичная заделка с выпуском верхней обшивки; в — то же, с выпуском нижней обшивки |
Общий коэффициент
Т
Светопропускания т0 ограждений не должен быть ниже 0,35.
Расчет общего коэффициента светопропускания панелей из стеклопластиков производится по формуле
Т = kxx т2 т3 т4, (5.125) где K — коэффициент, учитывающий старение стеклопластиков, принимается равным:
|
|
![]()
|
Т |
При однослойных конструкциях — 0,90;
При двухслойных и трехслойных с ребристым средним слоем — 0,85;
При трехслойных со средним слоем из волнистого стеклопластика — 0,80;
|
, здесь Тр Ti |
|
Ко- |
|
(ysctfa |
|
Рис. 5.31. График значений коэффициента т2 |
|
Эффициенты светопропускания соответственно обшивок и среднего слоя панели; |
|
Рис. 5.30. График значений коэффициента т2 |
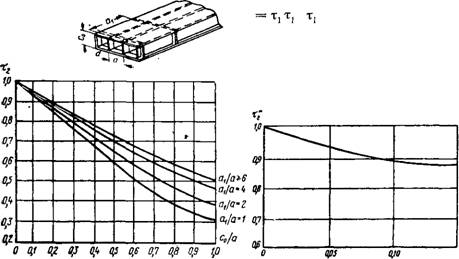
Коэффициент светопропускания стеклопластиков, образующих панель при однослойных панелях принимается равным свето - пропусканию одного листа стеклопластика; при двухслойных и трехслойных с ребристым средним слоем определяется из выражения Tj = т[т'2, здесь Т'г и т2 —коэффициенты светопропускания соответственно наружной и внутренней обшивок панели; при трехслойных со средним слоем из волнистого стеклопластика — из выражения Xl =
Т2—коэффициент, учитывающий затемнение конструктивными элементами панели и определяемый: при однослойных и двухслойных панелях по формуле
Т8 = 0,95 , (5.126)
•^общ
Здесь Snp — площадь светопропускающей части панели; S06m — площадь светопроема в свету; 0,95 — поправочный коэффициент, учитывающий толщину затемняющих элементов; при трехслойных панелях с ребристым средним слоем — по формуле Т2 = т2Т2, здесь х2 и х2 определяются соответственно по
Рис. 5.30 и 5.31;
Т3— коэффициент, учитывающий понижение светопропускания за
Счет загрязнения панели; т4—коэффициент, учитывающий затемнение светопроема фермами, балками, пересекающими светопроем и прочими конструктивными элементами. Значение коэффициентов т3 и т4 принимается согласно работе [48].