СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Оценки качества
В новейшей литературе, посвященной автоматическому управлению, подчеркивается важность математической формулировки понятия качества системы управления и методов его оценки. Современная теория управления предполагает, что инженер способен количественно определить требуемое качество системы. Количественная оценка качества крайне важна для работы адаптивных систем управления, для автоматической оптимизации параметров систем управления и для синтеза оптимальных систем.
Оценка качества — это численный показатель качества системы, который выбирается так, чтобы подчеркнуть наиболее важное требование, предъявляемое
к системе.
Система считается оптимальной системой управления, если ее параметры выбраны таким образом, что оценка качества принимает экстремальное (обычно минимальное) значение. Чтобы оценка качества имела реальный смысл, она должна представлять собой число, которое всегда положительно или равно нулю. Тогда наилучшей системой будет та, в которой эта оценка имеет минимальное значение.
Одним из видов оценки качества может служить интеграл от квадрата ошибки (ИКО), который определяется как
ИКО= fV(r)dr. (5.37)
Jo
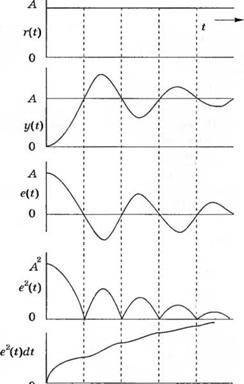
Верхний предел интегрирования Т выбирается достаточно произвольно, так, чтобы интеграл стремился к конечному значению. Обычно удобно выбирать Т равным времени установления Ts. На рис. 5.25 (б) изображена реакция некоторой системы управления с обратной связью на ступенчатое воздействие, а на рис. 5.25 (в) изображен график ошибки системы. Соответственно на рис. 5.25 (г) приведен график квадрата ошибки, а на рис.5.25 (д) — интеграла от квадрата ошибки. Этот критерий позволит выделять системы с очень большим и очень малым затуханием. Минимальное значение интеграла будет иметь место при компромиссном коэффициенте затухания. Оценка (5.37) удобна в практическом применении, т. к. легко могут быть реализованы схемы возведения в квадрат. К тому же квадрат ошибки удобен с математической точки зрения при аналитических расчетах и вычислениях на ЭВМ.
Другим легко используемым видом оценки качества является интеграл от модуля ошибки (ИМО), имеющий вид
ИМО= Ґ e(t)dt. (5.38)
Jo
Этот показатель в частности удобен при имитационном моделировании систем на компьютере.
Чтобы уменьшить вклад большой начальной ошибки в интеграл (5.38) и учесть ошибку, появляющуюся в дальнейшем, была предложена следующая оценка:
ИВМО= f7 te(t)dt, (5.39)
Jo
которая определяется как интеграл от взвешенного модуля ошибки (ИВМО). Весьма схожим показателем является интеграл от взвешенного квадрата ошибки (ИВКО):
ИВКО= te2(t)dt. (5.40)
Jo
Рис. 5.25
|
|
|
и |
Вычисление интеграла от квадрата ошибки
|
б) |
|
в) |
|
г) |
|
д) |
а)

Оценка качества ИВМО является наилучшей из рассмотренных, т. к. с ее помощью проще всего находить минимальное значение интеграла при изменении параметров системы. В общем случае интеграл, оценивающий качество системы, имеет вид
1 = f, (5.41)
Jo
где/есть функция ошибки, входного и выходного сигналов, а также времени. Используя различные комбинации переменных системы и времени, можно получить много разных оценок качества. Отметим только, что практическую ценность чаще всего представляют оценки ИМО и ИКО. Например, минимизация одной из оценок качества может быть непосредственно связана с минимизацией расхода топлива самолетом или космическим аппаратом.
Оценки качества играют большую роль при анализе и синтезе систем управления. Их использование мы проиллюстрируем двумя примерами.
Пример 5.6. Критерии качества
На рис 5.26 изображена одноконтурная система управления, где принято нормированное значение собственной частоты а>„ = 1. Замкнутая система имеет передаточную функцию
1
|
|
|
|
|
т О |
|
0.0 0.4 |
|
0.8 1.2 С |
|
1.6 2.0 |
|
Рис. 5.26. Одноконтурная система управления |
|
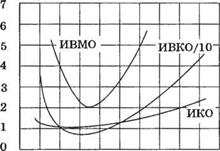
Рис. 5.27. Три оценки качества для системы второго порядка |
|
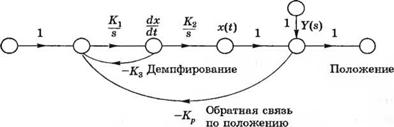
На рис. 5.27 представлены три оценки качества — ИКО, ИВКО и ИВМО, вычисленные для различных значений коэффициента затухания при ступенчатом входном воздействии. Эти кривые показывают хорошую избирательность оценки ИВМО по сравнению с показателем ИКО. На основе оценки ИВМО целесообразно выбрать значение коэффициента затухания Q = 0,7, что для данной системы второго порядка обеспечивает наиболее быстрое протекание переходного процесса с перерегулированием 4,6%. Пример 5.7. Система управления орбитальным телескопом На рис 5.28 изображен сигнальный граф системы наведения орбитального телескопа. Требует - ся выбрать значение коэффициента Къ, позволяющее минимизировать влияние возмущения D(s). которое в данном случае эквивалентно начальной ошибке по положению. Передаточная функция замкнутой системы по отношению к возмущению, полученная с помощью формулы Мейсона, имеет вид: |
|
ЧІ+Л^зО |
|
sU+KJC j) |
|
Y(s) D(s) A (s) l+KlK3s~' + KlK2Kps-2 s2+KtKis + K]K2Kp |
|
(5.43) |
|
Коэффициенты имеют следующие типичные значения: К, = 0,5 и К1К2Кр = 2,5. Следовательно, собственная частота аппарата fn = - fl3l2n = 0,25. При единичном ступенчатом возмущении минимальное значение оценки ИКО можно вычислить аналитически. Положение у(t) описывается выражением VIo' |
|
(!<**) |
|
е-0,25К,1 5щ |
|
(5.44) |
|
у(<) = |
|
где Р = K^(K2/tt)- 5. Возведение >’(/) в квадрат и интегрирование дает: |
|
к |
|
10 |
|
|.,+¥ |
|
°10 - о |
|
■-с |
|
-0£К31 |
|
^ sin2 |
|
—cos(Br + 2w) 2 2 |
|
dt = -- + 0,lK,. |
|
(5.45) |
|
Р* U ) •'opz Продифференцировав (5.45) и приравняв результат нулю, получим: |
|
di dK, |
|
= - Kl + 0,1 = о |
|
(5.46) |
|
Таким образом, минимум ИКО имеет место при К3 = VTo = 3,2. Это значение Къ соответствует коэффициенту затухания Q = 0,50. На рис. 5.29 приведены графики оценок ИКО и ИМО. Мини- |
|
°) Возмущение D(s)
|
б)
|
|
|
R(s) |
|
Возмущение D(s) |
|
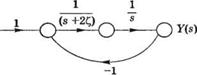
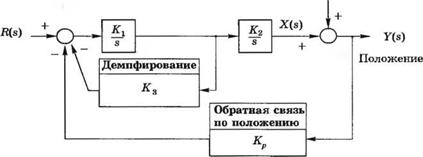
Рис. 5.28. Система управления наведением орбитального телескопа. (а) Структурная схема, (б) Сигнальный граф |
|
2 3 4 56789 10 Кя |
Рис. 5.29 1.5
Оценки качества системы управления. 3
орбитальным телескопом
в зависимости от параметра Аз 1.1
0.9 0.7 0.5
мум ИМО получается при Къ = 4,2 и С, = 0,665. Хотя критерий ИКО и не столь избирателен, как ИМО, тем не менее очевидно, что минимум этой оценки может быть вычислен аналитически. Что касается минимума ИМО. то он находится путем измерения этого показателя для нескольких значений варьируемого параметра системы.
Если выбранная оценка качества принимает минимальное значение, то система считается оптимальной. Однако оптимальные значения параметров непосредственно определяются тем, на основании какой оценки качества они получены. Так, в примерах 5.6 и 5.7 мы обнаружили, что оптимальная настройка системы является разной для разных оценок качества.
Для передаточной функции замкнутой системы общего вида
|
Г(*)_ R(s) sn+h |
|
(5-47) |
|
T(s) = |
|
'n-ls" ' +---+Ьі5+ ^0 |
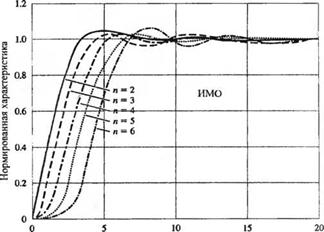
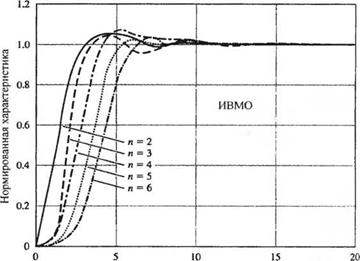
были определены значения коэффициентов, которые минимизируют оценку ИВМО в случае ступенчатого входного сигнала. Заметим, что подобная система обладает нулевой установившейся ошибкой, а ее передаточная функция имеет п полюсов и не содержит нулей. Оптимальные значения коэффициентов по критерию ИВМО приведены в табл. 5.6. На рис. 5.30 изображены переходные характеристики, соответствующие оптимальным значениям коэффициентов для критериев ИКО, ИМО и ИВМО, причем графики построены в зависимости от нормированного времени, соКроме рассмотренных, сушествуют и другие оценки качества, которые могут помочь проектировщику при решении конкретной задачи выбрать область изменения коэффициентов. Ниже приводится заключительный пример, иллюстрирующий использование оценки ИВМО.
|
Рис. 5.30 Переходные характеристики, соответствующие оптимальным коэффициентам нормированной передаточной функции, для критериев (а) ИКО, (б) ИМО, (в) ИВМО. Характеристики изображены в зависимости от нормированного времени, (!)„/. |
|
а) |
|
|
|
10 Нормированное время |
|
20 |
|
(rhk .......... / / /.......... V. |
|||
|
rrf h I 1 ; !i1 / |
|||
|
//tf/- |
-n = 2 л — 3 |
ИКО |
|
|
14 rf- її і!— /// // |
**■ n — 5 - n = 6 |
||
|
! і І! и / 11 ч |
|||
|
ft /7 / // // W4S |
|
1.0 |
|
0.8 |
|
* 0.6 |
|
о 0.4 |
|
0.2 |
|
15 |
|
1.2 |
Рис. 5.30
|
Нормированное время |
|
в) |
(продолжение)
Пример 5.8. Управление двумя камерами
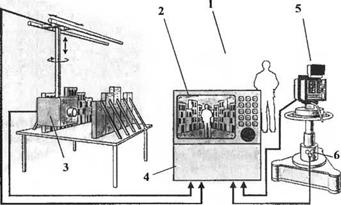
Чтобы дать возможность актерам выступать на фоне сложных миниатюрных декораций, необходима высокоточная и быстродействующая система управления. На рис. 5.31(a) изображена такая система, состоящая из двух камер, одна из которых направлена на актера, а другая — на миниатюрную декорацию.
Задача состоит в получении быстрой и точной координации двух камер путем использования информации, поступающей отдатчика, связанного с камерой переднего плана, для управления движением камеры заднего плана. На рис 5.31(6) приведена структурная схема системы управления движением камеры заднего плана по одной оси.
Замкнутая система имеет передаточную функцию
T{S) = ~j------------------------ KaK, A--------------------------------------------------------------- (54g)
s + 2Cfn0s + <»„s + KaKm4)f,
В соответствии с табл. 5.6, для системы третьего порядка необходимо выполнение условий:
2С<»>0 = 1,75<о„, Шо = 2,15со2, КаК„, ш2 = ш3.
Таблица 5.6. Оптимальные значения коэффициентов T^s), основанные на критерии ИВМО, при ступенчатом входном сигнале
■У + (О„
s2 + I,4toHs + o)jj .у3 + 1,75(0,,s2 + 2,15to^s - ь со,3, s4 + 2,1(0,+ 3,4 и,]s2 + 2,7(0, ss + 2,8(о,^ + 5,0(о,;s3 + 5,5(o3rv2 + 3,4 + (of,
j6 + 3,25(o, fv5 + 6,60(o, У + 8,60(o, У + 7,4 5(o, У + 3,95(0+ со*
Из рис. 5.30(e) мы видим, что для и = 3 время установления (нормированное) равно приблизительно 14 с. Следовательно, = 8. Поскольку желательно иметь как можно большее быстродействие, то (о„ следует выбрать достаточно большим, чтобы время установления было менее 1 с. Поэтому примем ю„ = 10 рад/с. Тогда согласно критерию ИВМО параметры Г(х) должны быть следующими:
ш0 = 14,67 рад/с и С, = 0,597.
Далее определяем коэффициент усиления усилителя и двигателя:
КЛт=4 = -^ = ^ = 4.65.
Шо 2,15т;; 2,15
В результате передаточная функция замкнутой системы принимает окончательный вид:
ГМ-j___________ Ш----------------------- =----------------------------------- Ш-------------------------------------- . (5.49)
s + 17,5s + 215s+ 1000 (s+ 7,08)(s+ 5,21+ >10,68)(s+ 5,21- yiO.68)
|
|
Положение полюсов замкнутой системы, предписываемое критерием ИВМО, приведено на рис. 5.32. Комплексным полюсам соответствует коэффициент затухания С, = 0,44, однако эти полюсы не являются доминирующими. Действительная реакция на ступенчатое входное воз-
Я)
|
Камера заднего плана |
|
Положение камеры заднего плана |
|
Положение камеры_____ |
|
б) |
|
переднего плана |
|
Усилитель |
Двигатель |
|
|
К |
кт |
|
|
S |
|
О |
|
s2 + 2£w0s + |
Рис. 5.31. Камера переднего плана, которая может быть либо кино - либо видеокамерой, направлена на голубой вогнутый экран. Электронная следящая система позволяет управлять одновременно двумя камерами. Камера заднего плана нацелена на миниатюрную декорацию и одновременно с помощью перископических датчиков воспроизводит в миниатюре все движения камеры переднего плана. Видеоконтроллер позволяет объединять изображения и вести их прямую запись.
1 — голубой матовый экран, 2 — видеоконтроллер, 3 — камера заднего плана,
4 — электронная система управления, 5 — камера переднего плана, 6 — датчики
действие, полученная путем компьютерного моделирования, показывает, что перерегулирование составляет всего 2%, а время установления (до вхождения реакции в зону 2% от конечного значения) равно 0,75 с.
Для передаточной функции замкнутой системы общего вида
+ b0
|
(5.50) |
7» = -
sn + bft_xsri~ +...+bfi + bQ
были определены значения коэффициентов, которые минимизируют оценку ИВМО в случае линейного входного сигнала. Заметим, что такая система отрабатывает линейный входной сигнал с нулевой установившейся ошибкой. Оптимальные значения коэффициентов приведены в табл. 5.7. Передаточная функция (5.50) предполагает, что G(s) содержит два или более интегратора, как и требуется для получения нулевой установившейся ошибки.
|
]<о
|
Рис. 5.32
Полюсы замкнутой системы, дающие минимум ИВМО
Таблица 5.7. Оптимальные значения коэффициентов T^s), основанные на критерии ИВМО, при линейном входном сигнале
s2 + 3,2rnirs + а>2 s3 + l,75coirs2 + 3,25co^s + я4 + 2,41cojrs3 + 4,93fi)^s2 + 5,14rn^s + to4 ss + 2,19ct„s4 + 6,50e4s3 + б. ЗОш^2 + 5,24to4s + to*