Second law analysis

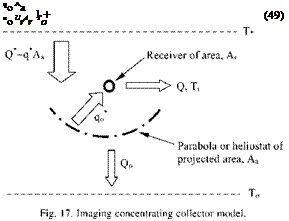
Tr. The remaining fraction Qo represents the collector - ambient heat loss:

Qo = Q* - Q (46)

For imaging concentrating collectors Qo is proportional to the receiver-ambient temperature difference and to the receiver area as:

Qo = UrAr(Tr - To) (47)

The analysis presented here is based on Bejan’s work [105,106]. The analysis however is adapted to imaging collectors because entropy generation minimisation is more important to high temperature systems. Consider that the collector has an aperture area (or total heliostat area) Aa and receives solar radiation at the rate Q* from the sun as shown in Fig. 17. The net solar heat transfer Q* is proportional to the collector area Aa and the proportionality factor q* (W/ m2) which varies with geographical position on the earth, the orientation of the collector, meteorological conditions and the time of day. In the present analysis q* is assumed to be constant and the system is in steady state, i. e.

Q* = q* Aa (44)

where Ur is the overall heat transfer coefficient based on Ar. It should be noted that Ur is a characteristic constant of the collector.

Combining Eqs. (46) and (47) it is apparent that the maximum receiver temperature occurs when Q = 0, i. e. when the entire solar heat transfer Qp is lost to the ambient. The maximum collector temperature is given in dimension­less form by:

(48)

o

Combining Eqs. (45) and (48):

For concentrating systems q* is the solar energy falling on the reflector. In order to obtain the energy falling on the collector receiver the tracking mechanism accuracy, the optical errors of the mirror including its reflectance and the optical properties of the receiver glazing must be considered.

Therefore, the radiation falling on the receiver qo is a function of the optical efficiency, which accounts for all the above errors. For the concentrating collectors, Eq. (33) can be used. The radiation falling on the receiver is:

* *

qo = no q

(45)

The incident solar radiation is partly delivered to a power cycle (or user) as heat transfer Q at the receiver temperature

= 1 +

(50)

Q,

(51)

S

gen

Qo Q

To Tr

Q

T,

(54)

Therefore, hc is a linear function of collector temperature. At stagnation point the heat transfer Q carries zero exergy or zero potential for producing useful work.

This equation can be written with the help of Eq. (46) as:

S

gen =

TO[Q'( 1 -1) — Q(■ — Tf)]

(55)