Solar energy in progress and future research trends

Unrestricted model

An alternative unrestricted method (UM) is proposed by §en [128] for preserving the means and variances of the global irradiation and the sunshine duration data.

In the restrictive regression approach (Angstrom equation), the cross-correlation coefficient represents only linear relationships. By not considering this coeffi­cient in the UM, some nonlinearity features in the solar irradiation-sunshine duration relationship are taken into account. Especially, when the scatter diagram of solar irradiation versus sunshine duration does not show any distinguishable pattern such as a straight-line or a curve, then the use of UM is recommended for parameter estimations.

All the aforementioned equations are based on the classical least squares estimation, which has hidden restrictive assumptions of the linearity, normality, homo - scadascity, correlation coefficient and error free data measurements [15]. Nonlinear models (Eqs. (41)-(44)) are based on nonlinear regression technique, which impose further assumptions on the parameter estimations. Hence, it is expected that all these models are affected by a set of assumptions, the validity of which are almost not checked in any practical study. It is therefore, necessary to provide a simple model, which will not require the restrictive assumptions.

In practice, the estimation of model parameters is achieved most often by the least squares method and regression technique using procedural assumptions and restrictions in the parameter estimations. Such restrictions, however, are unnecessary because procedural restrictions might lead to unreliable biases in the parameter estimations. One critical assumption for the success of the regression equation is that the variables considered over certain time intervals are distributed normally, i. e. according to Gaussian probability distribution function. As the time interval becomes smaller, the deviations from the Gaussian (normal) distribution become greater. For example, the relative frequency distribution of daily solar irradiation or sunshine duration is more skewed compared to the monthly or annual distributions. On the other hand, the application of the regression technique to Eq. (36) imposes linearity by the cross-correlation coefficient between the solar irradiation and sunshine duration data. However, the averages and variances of the solar irradiation and sunshine duration data play predominant role in many calculations and the conservation of these parameters becomes more important than the cross-correlation coefficient in any prediction model. In Gordon and Reddy [48], it is stated that a simple functional form for the stationary relative frequency distribution for daily solar irradiation requires knowledge of the mean and variance only. Unfortunately, in almost any estimate of solar irradiation by means of computer software, the parameter estimations are achieved without caring about the theoretical restrictions in the regression approach. This is a very common practice in the use of the Angstrom equation.

The application of the regression technique to Eq. (36) for estimating the model parameters from the available data

leads to [16]	to the following equations
(£) =a' + b'(S0) - and Va^H/H) = b'2 Var(S/S0) (51) where for distinction the unrestrictive model parameters are shown as a' and b', respectively. These two equations are the basis for the conservation of the arithmetic mean and variances of global solar irradiation and sunshine duration data. The basic Angstrom equation remains unchanged whether the restrictive or unrestrictive model is used. Eq. (50) implies that in both models the centroid, i. e. averages of the solar irradiation and sunshine duration data are equally preserved. Furthermore, another implication from this statement is that both models yield close estimations around the centroid. The deviations between the two model estimations appear at solar irradiation and sunshine duration data values away from the arithmetic averages. The simultaneous solution of Eqs. (50) and (55) yields parameter estimates as b'= / Var(H/H) (52) Var(S/S0) and
(46)
(47)
where rhs is the cross-correlation coefficient between global solar irradiation and sunshine duration data, Var() is the variance of the argument; and the overbars, (-) indicate arithmetic averages during a basic time interval. Most often in solar engineering, the time interval is taken as a month or a day and in rare cases as a season or a year. As a result of the classical regression technique, the variance of predic - tand, given the value of predictor is Var[(H/H0)/(S/S0) = S/S0] = (1 _ r2)Var(H/H0) (48)
This expression provides the mathematical basis for interpreting r;?s as the proportion of variability in (H/H0) that can be explained by knowing (S/S0). From Eq. (48), one can obtain after arrangements
Var(H/H0) _ Var[(H/H0)/(S/S0) = S/S0] Var(H7H)
(49)
If, in this expression the second term in the numerator is equal to 0, then the regression coefficient will be equal to 1. This is tantamount to saying that by knowing S/S0, there is no variability in (H/H0). Similarly, if it is assumed that Var[(H7H0)/(S/S0) = (S/S0)] = VarF/H), then the regression coefficient will be 0. This means that by knowing (OVERLINEMATHMODEONLYS/S0), the variability in (H/H0) does not change. In this manner, r2 can be interpreted as the proportion of variability in (H/H0), that is explained by knowing (S/S0). In all these restrictive interpretations, one should keep in mind that the cross­correlation coefficient is defined for joint Gaussian (normal) distribution of the global solar irradiation and sunshine duration data. The requirement of normality is not valid, especially if the period for taking averages is less than one year. Since, daily or monthly data are used in most practical applications, it is over-simplification to expect marginal or joint distributions to abide with Gaussian (normal) function. There are six restrictive assumptions in the regression equation parameter estimations such as used in the Angstrom equation that should be taken into consideration prior to any application [66]. These six restrictions in the solar irradiation estimation are normality, linearity, conditional distribution means, homoscedascity (variance constancy), autocorrelation and lack of measurement error [128]. The unrestricted parameter estimations require two simultaneous equations since there are two parameters to be determined. The average and the variance of both sides in Eq. (36) lead without any procedural restrictive assumptions
Ft Var(H/H0) S H Var(S/S0) S0
(53)
a
Physically, variations in the solar irradiation data are always smaller than the sunshine duration data, and consequently, Var(S/S0) $ Var(H/H0) For Eq. (52) this means that always 0 # b' # 1. Furthermore, Eq. (52) is a special case of Eq. (46) when rhs = 1. The same is valid between Eqs. (47) and (53). In fact, from these explanations it is clear that all of the bias effects from the restrictive assumptions are represented globally in rhs, which does not appear in the unrestrictive model parameter estimations. The second term in Eq. (53) is always smaller than the first one, and hence a is always positive. The following relationships are valid between the restrictive and unrest­rictive model parameters b b' = — (54) rhs and

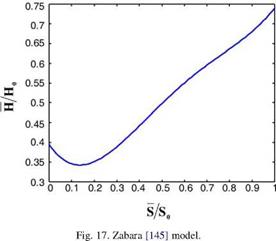
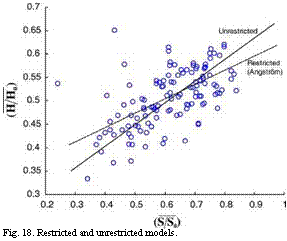
on a Cartesian coordinate system (Fig. 18). As mentioned previously two methods almost coincide practically around the centroid (averages of global solar irradiation and sunshine duration data). This further indicates that under the light of the previous statement, the unrestricted model overestimates compared to the Angstrom estimations for sunshine duration data greater than the average value and underestimates the solar irradiation for sunshine duration data smaller than the average. On the other hand, Eq. (55) shows that a' < a. Furthermore, the summation of model parameters is

a + b 1 H

rhs rhs H0

These last expressions indicate that the two approaches are completely equivalent to each other for rhs = 1. The new model is essentially described by Eqs. (50), (54) and (55). Its application supposes that the restricted model is first used to obtain a', b and r. If r is close to 1, then the classical Angstrom equation coefficients estimation with restrictions is almost equivalent to a' and b'. Otherwise, the new model results should be considered for application as in Eq. (50).

Through the unrestricted model, it has been observed that in the classical regression technique, requirements of normality in the frequency distribution function and of linearity and the use of the cross-correlation coefficient are imbedded unnecessarily in the parameter estimations. Assumptions in the restrictive (Angstrom) model cause overestimations in the solar irradiance amounts as suggested by Angstrom for small (smaller than the arithmetic average) sunshine duration and underestimations for large sunshine duration values. Around the average values solar irradiation and sunshine duration values are close to each other for both models, however, the unrestricted approach alleviates these biased-estimation situations. Additionally, the suggested unrestricted model includes some features of non-linearity in the solar energy data scatter diagram by ignoring consideration of cross-correlation coefficient.