Solar energy in progress and future research trends
Power solar radiation model
As explained above, there are many effects, which render the relationship between the solar terrestrial irradiation and the sunshine duration data into a nonlinear character This physical basis poses questions about the validity of basic Angstrom model in Eq. (36) for all the practical cases in the world. It is a physical fact that whatever the possibilities of nonlinear characters, these are reflected either in the sunshine duration or terrestrial solar irradiation measurements. Hence, it may not be physically plausible to suggest nonlinear models by adding integer valued power terms other than 1 as in Eqs. (41)-(44). However, the following type of power model is suggested first time in this paper
H
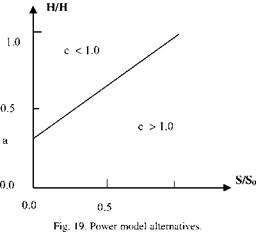
Ho0 where the exponent c reflects all the possible atmospheric non-linearity effects in the relationship between the global solar terrestrial irradiation and sunshine duration data. It is not necessary that c should have integer value. In fact, in natural occurrences, it should have non-integer values. In Eq. (57), a and b have the same physical interpretations as in for the classical Angstrom approach (Eq. (36)). It is known that a corresponds to the relative diffuse radiation on any overcast day and the summation of a and b represents the relative cloudless-sky global irradiation. This means that a and b parameters are reflections of extreme states which are full overcast, and completely cloudless cases. Hence, the power model as defined in Eq. (57) does not change the physical meanings of a and b. The extreme cases in the Angstrom formulation are also preserved in this a model. The power c provides the whole expected dynamism from the modeling. It is a parameter that represents the most occasional situations between the two extreme cases. It is obvious mathematically that power model reduces to Angstrom equation, if c = 1. Any nonlinear effect due to the atmospheric composition, the joint behaviors of irradiation and sunshine duration phenomena are reflected in this power value. Depending on the values of c different non-linearity trends are accounted in the power model in Fig. 19. There are two ways of determining the three model parameters in Eq. (57) from the available global solar irradiation and sunshine duration data at a given site.
The first approach benefits from the features of the classical Angstrom model. As already explained in Section 10.1, since the two parameters, namely, a and b, are equivalent to Angstrom coefficients at extreme cases, one will expect that these parameters will have the same values at the two boundary cases, i. e. for very low (S 0 0) and high (S 0 S0), values. It is, therefore, necessary to determine the Angstrom coefficient values through any available technique in the literature by using Eq. (40). The regression technique is the most commonly used tool in practice for estimating Angstrom coefficients. Hence, a and b values will be known. Subsequently, the substitution of these values
|
|
into Eq. (57) leaves one unknown, which is the power. Angstrom parameters are substituted into Eq. (57) and then by taking the logarithms on both sides the global estimate of c can be calculated as
c=log( S0 H2 a)2 log b] (58)
This is the mathematical formulation way of determining the power value.
Another way of finding power model parameters is through trial-and-error method where the Angstrom model parameter estimations (a and b) are not known. For this purpose, a set of plausible a and b values are taken as initial parameter values and subsequently (S/S0)i data are plotted versus [(H/H0)i 2 a]/b values on a double logarithmic paper. Of course, the scatter of points might not yield to a straight-line on the double logarithmic paper, and accordingly, the values of a and b are adjusted to have another scatter diagram with the improvement towards a better straight-line. The repetition of this procedure with different a and b values is continued until the best straight-line is obtained. The one that appears as the best straight-line on the double logarithmic paper provides automatically the estimates of a and b in addition to c value which is equal to the straight-line slope.