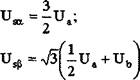В СИСТЕМАХ DTC
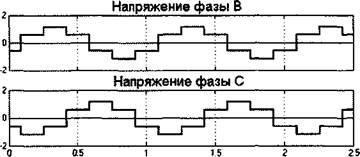
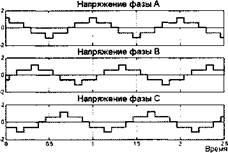
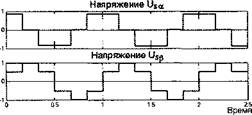
Фазные напряжения на выходе автономного инвертора - это ступенчатые функции, которые могут видоизменяться в зависимости от алгоритма управления электронными ключами. Изменения возникают в том случае, если в цикле переключений возникают паузы. На рис.1.2 показаны кривые изменения фазных напряжений при отсутствии коммутационных пауз в цикле работы автономного инвертора. Эти кривые полностью соответствуют той последовательности переключений, которая приведена в табл. 1.3.
Поскольку в дальнейшем все расчеты выполнены в системе относительных единиц, кривые на рис. 1.2, как и все последующие, построены при частоте 1 Гц и при амплитуде постоянного напряжения на входе, равной 1. Для анализа пространственного положения результирующего вектора выходного напряжения целесообразно перейти из трехфазной системы координат в эквивалентную ортогональную двухфазную, также неподвижную в пространстве и жестко связанную с направлением вектора напряжения фазы А, систему координат (а - (3). Это преобразование выполняется с помощью известных выражений:
|
Напряжение фазы А |
|
-г1--------------------- *--------------------- 1--------------------- •---------------------- L |
|
Время Рис. 1.2. Фазные напряжения на выходе автономного инвертора. |
При симметричном характере изменения фазных напряжений система уравнений (1.2) может быть преобразована к более простому виду. Благодаря этому при реализации системы управления можно обойтись без идентификации одного из фазных напряжений, например, напряжения фазы С. Преобразованная система уравнений выглядит следующим образом [17]:
|
|
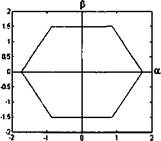
На рис.1.3 показаны кривые изменения во времени составляющих напряжения Usa и Us(3, соответствующие фазным напряжениям рис. 1.2.
|
Рис. 1.4. Годограф результирующего вектора напряжения на вы ходе автономного инвертора. |
Годограф имеет форму правильного шестиугольника, вершины которого соответствуют установившимся положениям результирующего вектора напряжения в пространстве в периоды между коммутациями электронных ключей. Если в кривых фазных напряжений присутствует пауза между положительной и отрицательной полуволнами, характер изменения положения результирующего вектора напряжения в простран-
стве изменяется в зависимости от продолжительности паузы
качественных изменений в годографе результирующего вектора напряжения не наблюдается, поскольку в кривых фазных напряжений сохраняется интервал одновременного включения трех электронных ключей. Просто длительность этого интервала сокращается. В качестве примера на рис.1.5 приведены кривые фазных напряжений при длительности паузы между полуволнами выходного напряжения автономного инвертора ДТ = 30 эл. град.
|
Рис. 1.5. Фазные напряжения на выходе автономного инвертора при длительности паузы между полуволнами АТ = 30 эл. град. |
Для построения годографа результирующего вектора выходного напряжения здесь также необходимо перейти из трехфазной системы координат в эквивалентную двухфазную. Сделать это можно с помощью выражений (1.2, 1.3) или, если исключить из системы уравнений (1.2) напряжение фазы А - с помощью выражений:
U** = “(Ub+Uc);
На рис. 1.6 показаны кривые изменения во времени составляющих напряжения Usa и Us(3, соответствующие фазным напряжениям рис.1.5.
Кривая изменения составляющей напряжения Usa, по-прежнему- повторяет в масштабе кривую изменения напряжения фазы А на выходе автономного инвертора. В то же время, кривая изменения составляющей напряжения Us(3 существенно изменилась. В ней появились шесть ярко выраженных участков длительностью 30 эл. град. в каждой полуволне. Тем не менее годограф результирующего вектора напряжения на выходе автономного инвертора свой характер не поменял - рис. 1.7.
|
|
•2 •' О I 2
Рис.1.7 Годограф результирующего вектора напряжения на вы ходе инвертора при длительности паузы между полуволнами АТ = 30 эл. град.
Годограф сохраняет форму правильного шестиугольника и ориентирован в координатной плоскости (а - (3) так же, как и годограф, приведенный на рис.1.4. Изменилась только амплитуда результирующего вектора напряжения.
Это объясняется тем, что при АТ > 60 эл. град, из алгоритма переключения электронных ключей автономного инвертора исчезает интервал одновременного включения трех электронных ключей. На рис. 1.8 приведены кривые фазных напряжений при граничной длительности паузы между полуволнами выходного напряжения АТ = 60 эл. град.
|
Напряжение фазы А
|
Рис. 1.8. Фазные напряжения на выходе автономного инвертора при длительности паузы между полуволнами АТ = 60 эл. град. Кривые фазных напряжений представляют собой последовательность прямоугольных импульсов длительностью 120 эл. град., со сдвигом между фазами 120 эл. град. и с интервалами между импульсами прямой и обратной полуволн АТ = 60 эл. град. Такая форма выходного напряжения широко использовалась в тиристорных преобразователях частоты с искусственной коммутацией второй половины прошлого века [7]. Составляющие напряжения в системе координат (а - (3) в этом случае имеют вид, представленный на рис. 1.9.
|
Рис. 1.9. Составляющие напряжения на выходе автономного инвертора в системе координат (а - (3) при длительности паузы между полуволнами АТ = 60 эл. град. |
Сопоставление этих кривых с кривыми, представленными на рис.1.3, показывает, что фазовый сдвиг между составляющими напряжения Usa и Us(5 90 эл. град., естественно, сохраняется, но форма кривых как бы поменялась местами. Теперь прямоугольный импульс, повторяющий в масштабе кривую изменения напряжения фазы А, соответствует составляющей напряжения USa, а составляющей напряжения Us(3 соответствует ступенчатая функция той же формы, которая присутствует в составляющей напряжения Usa при АТ = 0
Как видно из рис. 1.10, установившиеся положения результирующего вектора напряжения получили дополнительный фазовый сдвиг на угол 30 эл. град. Дальнейшее увеличение времени паузы между полуволнами фазных напряжений не приводит к качественным изменениям в характере годографа вектора результирующего напряжения.
В качестве примера на рис. 1.11 приведены кривые фазных напряжений при длительности паузы между полуволнами выходного напряжения автономного инвертора АТ = 75 эл. град. Теперь в них присутствует разрыв в каждой полуволне, так как коммутационные функции электронных ключей оказались сдвинуты друг относительно друга более, чем на 60 эл. град. Такое состояние инвертора не характерно для систем прямого управления моментом. Тем не менее, для сохранения общности рассмотрения вопроса об управлении автономным инвертором в системах DTC далее для этого случая приведены также графики составляющих напряжения в осях (а - (3) - рис. 1.12 и годограф результирующего вектора напряжения - рис. 1.13.
Годограф результирующего вектора выходного напряжения автономного инвертора сохраняет форму звезды Давида и ориентирован в координатной плоскости (а - (3) так же, как и годограф, приведенный на рис.1.10, но с уменьшением амплитуды результирующего вектора напряжения. В периоды пауз внутри полуволн составляющих напряжения Usa и Us(3 годограф обращается в ноль.
|
|
Таким образом, в системах прямого управления моментом частотно-регулируемого электропривода переменного тока преобразователь частоты представляет собой дискретное звено, имеющее шесть установившихся состояний и еще шесть промежуточных.
|
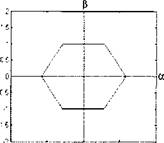
Рис. 1.14. Разбиение фазовой плоскости |
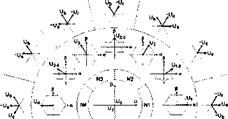
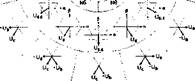
Поэтому при построении системы DTC фазовую плоскость в системе координат (а - (3) условно разбивают на шесть фазовых секторов. Сектора нумеруют от 1 до 6 по направлению вращения вектора потокосцепления статора асинхронного двигателя. Фактически каждый сектор соответствует определенной комбинации включенных электронных ключей. Размер сектора составляет 60 эл. град. Распределение секторов на фазовой плоскости и соответствующие им векторные диаграммы напряжений показаны на рис.1.14 [31].