ШИНЫ. НЕКОТОРЫЕ ПРОБЛЕМЫ ЭКСПЛУАТАЦИИ И ПРОИЗВОДСТВА
Математическое описание процессов, протекающих с выделением небольшого количества газов
Для определения температуры парогазовой смеси можно использовать уравнение теплового баланса для парогазовой фазы.
Рг„ • Сс„ • У.„с1Т = - ат • (т - Тж )• 80В ■ с1т -121 • рсм • Ссм • Т ■ (1т +
(1)
|
|
|
Ш |
|
П |
Левая часть уравнения (1) отражает результирующее изменение теплосодержания парогазовой смеси, первый член в правой части уравнения - подвод тепла за счет теплообмена с поверхностью источника газовыделения, второй член - отвод тепла
С удаляемой парогазовой смесью, третий член - подвод тепла с выделяющимися парами.
Плотность рсм и мольную теплоемкость смеси Ссм можно определить по правилу аддитивности, используя уравнение Менделеева-Клапейрона [458]:
TOC o "1-5" h z ш п
|
(2) |
![]() Х'Мш Рш+ 2^МГ] Сн
Х'Мш Рш+ 2^МГ] Сн
= .И
Рсм ^.7
|
П |
![]() Ш
Ш
|
Мш Рт |
![]()
|
МГ|' Р^ |
![]() 1+1 j=l
1+1 j=l
(3)
Ссм
Т п
Р ш + ^ Рг]
Ы }=1
Для жидкой или твердой фаз, в зависимости от типа технологического процесса, уравнение теплового баланса будет иметь вид:
Рж -Сж уж сГГж=яр ёх + ост (Т-Тж) Без ёх-
|
Гп п ^ 1пП+ ^ 1г 1] 1=1 ]=1 |
![]() Ш
Ш
|
СМ ЙСВ |
![]() •т-с1Т-8св^Л1пНАНу| (4)
•т-с1Т-8св^Л1пНАНу| (4)
1=1
Плотность и теплоемкость жидкой (твердой) фазы можно найти по формулам:
Ш
|
(5) |
![]()
|
Ж |
1 = 1
Ш
|
(6) |
![]()
|
Ж1 |
![]() Сж= 1Х[С
Сж= 1Х[С
Левая часть уравнения (4) отражает изменение теплосодержания жидкой или твердой фазы, первый член в правой части характеризует приток тепла в результате химической реакции, второй член - отвод тепла за счет теплообмена с парогазовой смесью, третий член - отвод тепла с удаляемой парогазовой смесью, четвертый член - затраты тепла на парообразование.
В уравнениях (1)-(6) фигурируют теплоты парообразования жидкостей и теплоемкости жидких, парообразных и газовых компонентов. Для расчета этих величин можно получить соответствующие уравнения.
Теплота парообразования чистою вещества определяется аналитически как решение уравнения:
|
ДН, |
![]()
|
(7) |
С!(1/Т)
Величину при нормальной температуре кипения можно определить по формуле [459]:
10,5
1
(8)
Подставив выражение (8) в(7) и выразив в явном виде величину АНУ, можно получить расчетную формулу для определения АНУ при нормальной температуре кипения [460]:
0,5
|
Рс * Тв |
|
АН |
|
Л/в |
|
|
|
|
|
|
Где Ку - эмпирическая константа, зависящая от температу-
|
Ры: |
![]() 1,04 при 200К<Т<300К Ку 1 1,045 при ТВ>300К.
1,04 при 200К<Т<300К Ку 1 1,045 при ТВ>300К.
Для учета зависимости теплоты парообразования от температуры можно использовать корреляцию Ватсона [461]:
|
0,38 |
|
1 ~ Тг2 1-Тп |
|
|
|
|
Подстановка (9) в (10) при условии дНу1=дНув, дНу2=дНу приводит к уравнению:
|
0,5 |
|
0,38 |
|
1_Тг2 |
|
(П) |
|
1-Тп. |
|
Рс-Тв |
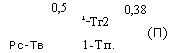 |
|
|
|
|
|
Таким образом можно вычислить теплоту парообразования 1-го компонента при произвольной температуре.
Для расчета теплоемкостей жидких компонентов при про - извольной температуре можно использовать следующую формулу [462]:
Сж (ТЖ)=А+В Тж+С Тж2 (12)
Константы А, В, С для различных веществ приводятся в таблицах [463].
Теплоемкости газов и паров при протекании технологического процесса будут изменяться в зависимости от давления. Поскольку теплоемкость связана с энтальпией соотношением
|
ДН |
![]() [464]:
[464]:
То изменение теплоемкости при изменении давления можно записать в виде:
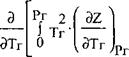
|
•<Ц1пРг) (14) - Рг |
![]() О
О
Ср Ср І
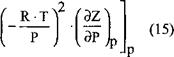 Последнее выражение после преобразований приводит к уравнению:
Последнее выражение после преобразований приводит к уравнению:
Э2Н э
|
|
Следует отметить, что теплоемкости газов и паров практически не зависят от температуры при постоянном давлении
[465].
Дифференциальные уравнения материального баланса могут быть получены по отдельным компонентам смеси. Для парогазовой смеси уравнение материального баланса по 1-му компоненту пара записывается в виде:
Іпіі $св - 1п2і Спі (ІТ — Усв (ІСпі (16)
Первый член в уравнении (16) отражает приток 1-го компонента паровой смеси в камеру за счет испарения ьго жидкого компонента с поверхности обрабатываемого изделия, второй член - отвод 1-го компонента паровой смеси из камеры в систему улавливания; правая часть уравнения (16) характеризует результирующее изменение парциальной концентрации ьго компонента паровой смеси.
Аналогично можно записать уравнение материального баланса по ]-му компоненту парогазовой смеси:
Г 1] $св с! т -1г2] Сг] .ёт - Усв (17)
Первый член в уравнении (17) отражает приток ]-го газового компонента в камеру за счет реакции в жидкой (или твердой) фазе, второй член - отвод ]-го газового компонента из камеры в систему улавливания; правая часть уравнения (17) характеризует результирующее изменение парциальной концентрации ^го газового компонента в камере.
|
СпГМа’Рв |
![]() Парциальные давления компонентов связаны с их массовыми концентрациями следующей формулой [466]:
Парциальные давления компонентов связаны с их массовыми концентрациями следующей формулой [466]:
(18)
Формула (18) справедлива как для паровых, так и для газовых компонентов.
В уравнения (16), (17) входят величины объемных производительностей системы улавливания токсичных выбросов по различным паровым и газовым компонентам. В общем случае связь объемной производительности с концентрацией компонента может быть выражена степенной зависимостью [467]:
(19)
|
С; |
![]()
|
М. |
![]() Где
Где
(20)
3=1 м ] »=1 м
121 = А-РП
|
(21) |
![]() В уравнения (16), (17) входят также величины парциальных потоков паровых и газовых компонентов 1п1Ь 1г1^Их можно рассчитать следующим образом.
В уравнения (16), (17) входят также величины парциальных потоков паровых и газовых компонентов 1п1Ь 1г1^Их можно рассчитать следующим образом.
Можно предположить, что совокупность жидких компонентов, содержащихся в обрабатываемом изделии, является идеальной системой. Тогда парциальные давления паровых компонентов вблизи поверхности обрабатываемого изделия могут быть записаны по закону Рауля для идеальных систем:
В соответствии с допущениями, принятыми в п. 5.3.1, давление паров чистого компонента рассчитывается по уравнению Антуана [ 468]:
Д._В[
Р01 = е (23)
При подстановке уравнения (23) в (22) получается формула для расчета парциальных давлений паровых компонентов над поверхностью обрабатываемого изделия при произвольной температуре:
|
Р. = х;е т <24> |
1 * ^
Дифференцирование обеих частей уравнения (24) приводит к формуле для расчета приращений парциальных давлений паровых компонентов над поверхностью изделия при изменении температуры на величину <1Т:
Ар. =хі~єАі т сіт + ах. • І 1 т2 і
|
Л_ВІ Аі р |
![]() Согласно принятым в п. 5.3.1 допущениям, компоненты парогазовой смеси подчиняются законам идеальных газов. Поэтому парциальная плотность компонента парогазовой смеси над поверхностью изделия может быть найдена по уравнению Менделеева-Клапейрона [458]:
Согласно принятым в п. 5.3.1 допущениям, компоненты парогазовой смеси подчиняются законам идеальных газов. Поэтому парциальная плотность компонента парогазовой смеси над поверхностью изделия может быть найдена по уравнению Менделеева-Клапейрона [458]:
|
(26) |
![]()
|
РІ |
![]() Рі’Мі ЯТ
Рі’Мі ЯТ
Дифференцирование обеих частей уравнения (26) приводит к:
|
(27) |
![]() Л Мі Рі - Мі <1Т
Л Мі Рі - Мі <1Т
' ят 1 я т2
После подстановки выражения (25) в (27), получается формула для расчета приращений парциальных плотностей паровых компонентов смеси над поверхностью обрабатываемого изделия при изменении температуры на величину с1Т:
|
Ві А‘ х Хі—Г‘е * сІТ + СІХІЄ Т2 |
|
М сіТ 77'^' |
|
Аі у |
|
(28) |
|
Аі- |
|
Мі Ят |
|
Фі |
В формулу (28) входит мольная доля компонента Х{. Для ее расчета необходимы следующие формулы.
Парциальная масса і-го жидкого компонента, содержащегося в обрабатываемом изделии, убывает в результате испарения по закону:
= ГП|0 ~ Всв Пп] |(Т)^Т
Мольная доля ьго компонента выражается через его парциальную массу соотношением [469]:
XI =-------- —----------------------- (30)
П 1П 1
|
Т 1 |
![]() ГП
ГП
]=1 М ] 1=1 1УП
Можно выразить массу 1-го парового компонента смеси через плотность и объем:
Тг Р* V (31)
Дифференцирование правой и левой части уравнения (31) по времени и деление их на площадь поверхности обрабатываемого изделия, приводит к следующему уравнению:
1 с! пгн _ V ^Р| /"*9^
£ с! т ~ Б с1т
Поскольку высота, объем и площадь поперечного сечения камеры связаны соотношением Н =У/8, а левая часть уравнения (32) представляет собой поток иго парового компонента, то это уравнение можно переписать в виде:
П11 ёх
Подставляя формулу (28) в (33), можно получить уравнение, позволяющее рассчитать парциальные потоки паров, выделяющихся с поверхности обрабатываемого изделия:
Парциальный поток ]-го газового компонента I, входящий в формулу (17), определяется следующим образом. Кинетическое уравнение реакции, протекающей внутри или на поверхностном слое обрабатываемого изделия, записывается в следующем виде [470]:
С (35)
Зависимость константы скорости химической реакции от температуры определяется законом Аррениуса:
— (36)
К = г-е кт
Подставляя (32) в (31) и учитывая, что интенсивность га - зовыделения пропорциональна скорости химической реакции и площади поверхности обрабатываемого изделия, можно получить:
Е
Т,.-7-е кт • С‘р|-С(рь<;
Агу ~ ^ с '-жк Ьизд