ПРИНЦИПЫ ЛАЗЕРОВ

ПРОДОЛЬНАЯ НАКАЧКА

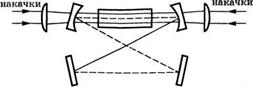
Для продольной накачки излучение диодного лазера обычно необходимо сфокусировать в активной среде в малое (с поперечным размером 0,1-1 мм) пятно по возможности кругового сечения. На рис.6.11 а-в представлены три наиболее распространенных лазерных конфигурации. На рис 6.11а показан лазерный стержень, помещенный в плосковогнутый резонатор; плоское зер­кальное покрытие нанесено непосредственно на тот торец стержня, на кото­рый фокусируется пучок накачки. На рис 6.116, в пучки накачки от двух разных диодных систем фокусируются с двух концов стержня в его центре. Резонатор лазера может иметь либо кольцевую конфигурацию в виде сло­женной петли (рис 6.116), либо линейную конфигурацию, с изломами в виде буквы «z» (рис. 6.Не). Для последних двух конфигураций ось резонатора обозначена пунктирной линией.

Зеркала с высоким коэффициентом отражения

Мі=йІ

V

Рис. 6.11

Типичные конфигурации продольной накачки излучением диодных лазеров:

А) накачка с одного конца стержня в простом плосковогнутом резонаторе; б) накачка с двух концов стержня для кольцевого резонатора сложенного типа и в) накачка с двух концов стерж­ня для 2-образного линейного резонатора.

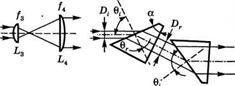Рис. 6.12

(а) Схема системы передачи излучения накачки однополоскового диодного лазера с компенсацией астигматизма; (б) простая анаморфотная система из двух цилиндрических линз; (в) анаморфотная пара призм

Рассмотрим теперь вопрос о том, каким образом для данных резонаторов преобразовать пучок излучения накачки так, чтобы внутри лазерного стерж­ня он имел наиболее близкое к круговому сечение подходящего размера.

Рассмотрим вначале однополосковый диодный лазер (рис. 6.9а), кото­рый используют как источник накачки для маломощных устройств. (С по­мощью накачки однополосковым лазером могут быть получены выходные мощности вплоть до десятков мВт.) Эллиптичность сечения сильно расходя­щегося пучка от лазерной полоски может быть скомпенсирована с помощью комбинации из двух сферических линз и анаморфотной оптической систе­мы, схематически изображенной на рис. 6Л2а прямоугольником. На этом рисунке сплошные линии показывают изменения продольного сечения пуч­
ка в плоскости р-п перехода диодного лазера; в свою очередь, пунктирные линии соответствуют изменениям такого сечения в плоскости, перпендику­лярной к плоскости р-п перехода. Линза Lx с фокусным расстоянием /* пред­ставляет собой короткофокусную сферическую линзу с большой числовой апертурой, предназначенную для коллимации сильно расходящегося пучка от лазерного диода. Поскольку 0± = 40ц, то поперечное сечение пучка после прохождения линзы имеет форму эллипса с размерами осей dL = 2/itan0Х (так называемая «быстрая» ось, перпендикулярная плоскости р-п перехода) и с/ц =2/х tan ©л («медленная» ось в плоскости р-п перехода). Таким образом, в типичном случае dL/d\ = tan Gj^/tan 6ц = 4. Коллимированный линзой пучок с эллиптическим поперечным сечением пропускают через анаморфотную оптическую систему, обеспечивающую различную степень расширения это­го пучка вдоль двух осей эллипса. Если, например, система обладает рас­ширением пучка 4:1 вдоль медленной оси и не изменяет поперечный размер пучка вдоль быстрой оси, то в результате такого преобразования получится пучок с круговым сечением. Возможно, наиболее просто такой анаморфот­ный расширитель можно получить, используя две цилиндрических линзы L3 и L4, установленных в конфокальной, или телескопической, конфигура­ции (рис. 6.126). Если две этих линзы фокусируют в плоскости, содержа­щей медленную ось, то результирующее расширение пучка составит /4//3, где f4 и /3 — фокусные расстояния линз для продольного сечения пучка в этой плоскости (сплошные линии). В то же время в ортогональной плоско­сти рассматриваемые цилиндрические линзы ведут себя по отношению к пуч­ку просто как плоскопараллельные пластинки, не влияя на его поперечный размер в направлении быстрой оси.

Однако анаморфотная система, показанная на рис. 6.126, не часто ис­пользуется на практике, поскольку для нее требуются хорошо скорректиро­ванные на аберрации линзы с высокой числовой апертурой, которые доволь­но дороги. Поэтому наибольшее распространение получила анаморфотная пара призм, показанная на рис. 6.12в [6]. Снова рассмотрим изменения по­перечных размеров пучка только в плоскости медленной оси (изображены на рисунке сплошными линиями). Используя простые геометрические сообра­жения, можно показать, что после преломления на передней поверхности первой призмы ширина падающего пучка увеличивается от Dt до Dr так, что Dr/Dj = cos 6r/cos 0г, где 6г и 0Г являются соответственно углами падения и преломления для поверхности призмы. Если задняя грань первой призмы почти перпендикулярна направлению пучка, то на ней не возникает прелом­ления, так что пучок проходит через нее без изменений. При таких условиях увеличение ширины пучка М после прохождения первой призмы составит

M = ^L = cos0L (6.3.1)

Д cos 0j

Рассмотрим теперь прохождение пучка через вторую призму. Если эта приз­ма идентична первой, ориентирована так, как показано на рис. 6.12в, а угол падения на входную грань снова равен 0*, то после прохождения второй приз­мы ширина пучка снова увеличится в М раз. Таким образом, результирующее увеличение ширины выходящего пучка составит М2, а его ось будет парал­лельна оси входящего, хотя и смещена в поперечном направлении. В плоско­сти быстрой оси две рассматриваемых призмы эквивалентны простым плоско­параллельным пластинкам и поэтому не приводят к уширению пучка. Таким образом, если в схеме, показанной на рис. 6.12а, использовать анаморфот­ную пару призм с подходящими величинами угла 0*, показателя преломле­ния п и угла при вершине а, то можно получить М = 2, т. е. полное увеличе­ние М2 — 4. Таким образом, сечение пучка после прохождения пары призм будет круговым. Если коллимирующая линза Ьх на рис. 6.12а имеет доста­точно большую числовую апертуру, чтобы пропустить сильно расходящийся вдоль быстрой оси пучок, и не имеет аберраций, то после этой линзы, а сле­довательно, и после пары призм, пучок полностью сохранит дифракционно­ограниченный характер первоначального пучка, выходящего из диодного лазера. Следовательно, расходимости вдоль двух осей оказываются теперь одинаковыми, поскольку после прохождения через пару призм пучок имеет круговое сечение. Используя сферическую линзу Ь2 с соответствующим фо­кусным расстоянием f2, можно сфокусировать это излучение в круглое пят­но нужного размера в фокальной плоскости линзы (рис. 6.11а), т. е. там, где удобно поместить активную среду. Если линза Ь2 также не имеет аберраций, то пучок в фокальной плоскости обладает круговой симметрией и является дифракционно-ограниченным.

Пример 6.2. Расчет анаморфотной пары призм для фокусировки излу­чения однополоскового диодного лазера. Рассмотрим систему, изображен­ную на рис. 6.12, и однополосковый лазер с 0± = 20° и 0ц = 5°. Предполагая при этом, что распределения интенсивности дифракционно ограничены и гауссовы, можно положить d± = 1,4 мкм и d\ = 5,8 мкм (X = 780 нм). Возь­мем коллимирующую линзу Lx с фокусным расстоянием fx = 6,5 мм. После линзы Ьг диаметры сечения пучка вдоль быстрой и медленной осей равны соответственно D± = 2/х tan 0± = 4,73 мм и 2)ц = 2/xtan 0ц = 1,14 мм. В этом случае каждая призма должна обеспечивать увеличение М = (D±/D^1/2 ^ 2. Предполагая, что призмы изготовлены из плавленого кварца, так что по­казатель преломления на длине волны ~800 нм равен п = 1,463, можно из соотношения (6.3.1) и закона Снеллиуса (sin 0* = nsin 0Г) определить углы 0* и 0Г. Их величины можно легко получить либо графически, либо с помо­щью быстрой итерационной процедуры. Для ее проведения присвоим уг­лу 0* некоторое начальное значение, а затем, используя закон Снеллиуса при п = 1,463, вычислим первое значение угла 0Г. Полученную величину подставим в соотношения (6.3.1)сМ = 2и вычислим новое значение уг­ла 0*, соответствующее первому шагу итерации, и т. д. Если начать, напри­мер, со значения 0* = 70°, то данная процедура через несколько итераций быстро сойдется к значениям 0f = 67,15° и 0r s 39°. Поскольку предполага­ется, что пучок выходит перпендикулярно ко второй грани призмы, то простое геометрическое рассмотрение показывает, что угол при вершине призмы должен быть равен а = 0Г = 39°. Таким образом, после второй приз­мы получается пучок кругового сечения с диаметром D = D± = 4,73 мм. Положим теперь фокусное расстояние линзы Ь2 равным /2 = 26 мм и до­пустим, что пучок остается дифракционно ограниченным после этой лин­зы. Размер пятна в фокальной плоскости второй линзы составит в таком случае <1 = 4f2lnD =5,52 мкм (здесь снова использовано выражение, от­носящееся к фокусировке гауссова пучка; см. формулу (4.7.28)). Отме­тим, что, в принципе, можно получить очень малое значение диаметра пучка накачки. Действительно, видно, что воздействие оптической сис­темы в плоскости быстрой оси (рис. 6.12а) сводится к созданию изобра­жения распределения интенсивности на выходном торце диодного лазера с /2//1 = 4-кратным увеличением. Поскольку <2Х = 1,4 мкм, то ожидается, что с1 = (f2/fl)dL = 5,6 мкм. Однако, для того чтобы получить такое малень­кое пятно, необходимо, чтобы используемые линзы, и особенно коллими­рующая линза Ьи были хорошо исправлены на сферическую аберрацию. В обычной ситуации, с учетом ограниченности разрешающих способностей линз Ь1 и Ь2, можно рассчитывать получить диаметр пучка в фокальной плоскости линзы Ь2 в 5-10 раз больше. В любом случае, из геометрических соображений, расходимость пучка в фокальной плоскости линзы Ь2 опре­деляется выражением 0 = £>/2/2, где В — диаметр пучка на линзе. Если вблизи фокальной плоскости помещен стержень из материала с показате­лем преломления Яд, то из-за преломления расходимость пучка в стержне будет примерно в пя раз меньше. Если теперь положить пЕ= 1,82, что соот­ветствует кристаллам Кс1:УАО, то получим 0П = D|2f2nIІ = 0,05 рад £ 3°.

Для линейки диодных лазеров шириной, например, 200 мкм, поскольку углы расходимости 0± и 0ц приблизительно такие же, как и в случае одиноч­ного полоскового лазера, конфигурация, показанная на рис. 6.12а-в, все еще может быть использована для получения круглого пятна после анаморфот­ной пары призм. Однако ввиду того, что расходимость пучка вдоль медлен­ной оси примерно в 40 раз больше дифракционного предела, пятно в фокаль­ной плоскости линзы Ь2 будет представлять собой эллипс с отношением осей 40:1. В соответствии с примером 6.2, в случае хорошо скорректированной на аберрации коллимирующей линзы Lx эллиптичный пучок может иметь раз­меры, например, 2,8 мкм х 112 мкм. В реальной ситуации аберрации опти­ческой системы, которые сильнее проявляются в направлении быстрой оси, приводят к более близкой к круговой форме пятна, с поперечными размера­ми порядка 150 мкм. Другой широко применяемый с линейками диодных лазеров способ доставки излучения накачки в активную среду связан с ис­пользованием многомодового оптического волокна. Для линейки шириной 200 мкм можно использовать волокно с диаметром сердцевины 200 мкм, непосредственно пристыкованное к ее выходной грани. Однако в такой кон­фигурации числовая апертура волокна NA (NA = sin 0Л где Qf — входная угловая апертура волокна) должна быть достаточно большой для того, что­бы обеспечить ввод в него сильно расходящегося пучка диода, т. е. должно выполняться соотношение sin 0^ > sin 0± = 0,4. После того как излучение прой­дет в волокне достаточно большое расстояние, сечение пучка на выходе из волокна становится круговым, а его расходимость становится равной число­вой апертуре волокна АГА, т. е. имеем Qout = Таким образом, в результате распространения по волокну расходимость вдоль медленной оси ухудшается от Qin = 0ц до 0ouf = 0^ s 0±. Для того чтобы уменьшить начальную расходимость пучка, между линейкой и волокном можно разместить сильно короткофо­кусную цилиндрическую линзу, коллимирующую пуч~к вдоль быстрой оси так, чтобы его ширина стала равной диаметру волокна. Тогда можно исполь­зовать волокно с числовой апертурой АТА, приблизительно равной расходи­мости пучка вдоль медленной оси, т. е. взять = 0±. В этом случае, который более подробно рассмотрен в примере 6.3, пучок от линейки шириной 200 мкм можно сфокусировать в волокно диаметром 250-300 мкм и числовой аперту­рой АТА = 0,1.

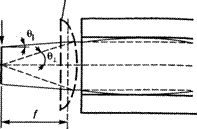
Пример 6.3. Фокусировка излучения линейки диодных лазеров в много­модовое оптическое волокно. Рассмотрим простую конфигурацию, изобра­женную на рис. 6.13, в которой цилиндрическая линза с малым фокусным расстоянием f коллимирует пучок вдоль быстрой оси (пунктирные ли­нии). Ширина пучка вдоль этой оси после линзы будет равна DL =2ftg 0±. В плоскости медленной оси цилиндрическая линза действует на пучок как плоскопараллельная пластинка и поэтому не влияет на его ширину вдоль этой оси (непрерывные линии). Для того чтобы отразить этот факт на рисунке, цилиндрическая линза изображена пунктиром, который пока­зывает, что она фокусирует только в плоскости быстрой оси. Ширина пучка в плоскости медленной оси после линзы будет примерно равна Z)||« La + 2/tg 0ц, где La — длина линейки. Если теперь задаться условием Щ = DL, то полу­чим, что f = La/2(tg 0± - tg 0ц). Полагая La = 200 мкм, 0Х = 20° и 0ц = 5°, нахо­дим, что f = 350 мкм. Такую величину фокусного расстояния можно полу­чить при использовании волоконных микролинз. При столь малом фокус­ном расстоянии диаметр пучка после линзы будет составлять D = D\ = D± = = 2/tg0± = 254 мкм, так что это излучение может быть легко введено, на­пример, в многомодовое волокно диаметром 300 мкм, сопряженное с микро­линзой. Если волоконная микролинза хорошо скорректирована, то расхо­димость пучка после нее будет преимущественно определяться нескомпен - сированной расходимостью пучка вдоль медленной оси. Таким образом, числовая апертура волокна должна составлять NA = sin 0/ > sin 0ц = 0,09. Рас­ходимость пучка излучения на выходе из волокна, если оно достаточно длин­ное, будет равна в этом случае числовой апертуре волокна.

В случае блока линеек диодных лазеров шириной 1 см можно применить одну цилиндрическую микролинзу длиной 1 см для того, чтобы сфокусиро­вать излучение каждой из линеек блока в отдельное многомодовое волок­но. Поскольку каждая диодная линейка имеет здесь характерную ширину 100 мкм (см. рис. 6.10а), то для них можно использовать волокна с диамет­ром сердцевины 200 мкм и числовой апертурой АТА = 0,1 (рис. 6.13). Таким способом можно ввести пучок от блока линеек в 20 волокон, концы кото­рых могут затем быть собраны в круглый жгут волокон диаметром 1-1,5 мм с суммарной расходимостью, равной числовой апертуре одного волокна (ЫА = 0,1). Пучок, испускаемый этим жгутом волокон, отображается на торец лазерного стержня вдоль одного (см. рис. 6.11а) или двух (рис. 6.116, в) продольных направлений. Было показано, что в такой конфигурации накач­
ки можно достичь полного пропуска­ния передающей системы до 85%. При использовании стержня из К(1:УУ04, накачиваемого двумя состыкованны­ми с волокном блоками лазерных ли­неек, были получены выходные мощ­ности до -15 Вт в моде ТЕМ00 с эффек­тивностью преобразования излучения в излучение -50%.

Был продемонстрирован также ин­тересный альтернативный подход, ко­торый позволяет изменить форму силь­но асимметричного пучка на выходе из линейки лазеров или блока линеек та­ким образом, чтобы получить одинаковые размеры и расходимости пучка вдоль заданных направлений быстрой (вертикальной) и медленной (гори­зонтальной) осей. Подход заключается в том, что пучок от линейки лазеров или блока линеек после коллимации волоконной линзой вдоль быстрой оси направляется на пару параллельных и наклоненных относительно оси пучка зеркал. Эта пара зеркал за счет многократных отражений эффективно делит первичный пучок на несколько вторичных, смещенных относительно друг друга в горизонтальном направлении, и направляет их друг над другом, фор­мируя таким образом на выходе из системы пучок прямоугольного сече­ния [7]. При выравнивании размеров пучка в горизонтальном и вертикаль­ном направлениях уменьшение интенсивности вторичных пучков в верти­кальном направлении компенсируется ее увеличением в горизонтальном направлении, так что в среднем обеспечивается равномерное распределение интенсивности в поперечном сечении суммарного пучка на выходе. Пучок с таким сечением дает возможность осуществлять очень интенсивную продоль­ную накачку, которая особенно эффективна для квази-трехуровневых лазе­ров с низким усилением, которые плохо накачиваются другими методами.