ПОЛУПРОВОДНИКОВЫЙ ЭЛЕКТРОПРИВОД
УПРАВЛЕНИЕ В СТАТОРНЫХ ЦЕПЯХ
2.1.1. ФАЗОВОЕ УПРАВЛЕНИЕ
При работе преобразователей в процессе фазового управления образуются схемы несимметричного подключения трехфазного асинхронного двигателя к питающей сети, в частности режим двухфазного включения. Для исключения периддинеских коэффициентов в диф^ереніШаТьнй^уравнениях, описывающих несимметричные режимы, необходимо, чтобы система координат была неподвижна относительно того элемента машины (статора или ротора), в котором возникает несимметрия. Поэтому выберем неподвижные координатные оси а, р(сок=0).
При рассмотрении короткозамкнутых асинхронных двигателей или двигателей с контактными кольцами при одинаковых сопротивлениях, включенных в фазы ротора, иаг=Щг=0.
|
Ucs UC U00' UCci |
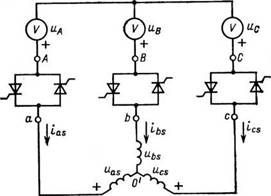
Расчетная схема для систем фазового управления в статоре приведена на рис. 2.1. Мгновенные значения фазных напряжений питающей сети (и а, ив, ис) описываются (2.11). В общем случае фазные напряжения статора (рис. 2.1) определяются следующим образом:
|
Ubs ив 1100' 11 вь |
|
Рис. 2.1. Расчетная схема для систем фазового управления в статоре: uas’ ubs< ucs ~ напряжение фаз статора |
где м0О, — напряжение между нулевыми точками питающей сети и обмотки статора; иАа{ивь, «се) — напряжение на тиристорах, включенных в фазу а(Ь, с статора.
|
(2.42) |
Как показано в [42], при симметричной трехфазной нагрузке И уравновешенной системе ТОКОВ (ias+ibs+*cs = 0)
^00' («а0 | «foo b wco)/3>
где иа0(иьо, tico)—напряжение между выводом фазы а(Ь, с) обмотки статора и нулевой точкой питающей сети.
|
(2.43) |
Как следует из рис. 2.1:
|
«ао |
UA" |
~UAa |
|
II О а |
ив~ |
~ ивъ |
|
г> о II |
иС иСс• |
При (ок==0 и совмещении фазы а статора с вещественной осью связь между проекциями обобщенных векторов статора (*as, и реальными фазными величинами (jeas, Xbs, *cs), как следует из
(2.4) , выражается в виде
х = хп
|
(2.44) |
as а
XVs=(Xbs—Xcs)/V3 •
Зная особенности различных схем фазового управления в статоре и используя (2.41) — (2.44), можно определить зависимость вектора напряжения асинхронной машины U от и№ и I. Учтем также, что для рассматриваемых схем матрица К=0, т. е. Ft= = Ri, а при выбранном значении toK однозначно определяются вектор Ujv и его проекции (2.13) и матрица Н (2.18).
Схема ЗТТ (см. рис 1.1,а). В этой схеме в течение одного периода питающего напряжения включаются в работу шесть тиристоров, и при симметричном управлении для фазных напряжений двигателя имеет место как полуволновая симметрия
|
(2.45) |
Has (т)= — Uas (*'+*)’. ubs (x) = — ubs (T + *); ucs (z) = — Ucs (*+*).
|
(2.46) |
так и трехфазная симметрия
Uas (T) = Ubs (z + 2іс/3) = Ucs (x — 2lt/3),
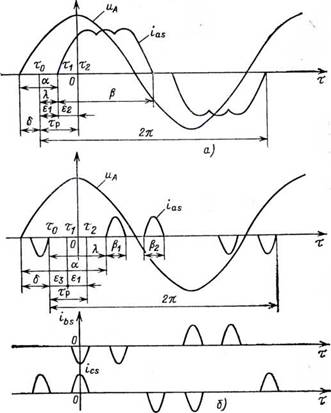
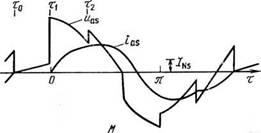
что обеспечивает шеститактную симметрию (g=6). Поэтому тР= = я/3, а /п=300 Гц (2.34). Как показано в [30, 37], при исследовании установившихся режимов этой схемы в качестве параметра управления целесообразно использовать не угол а, а параметр X (рис. 2.2), представляющий собой интервал между коммутациями тока сопряженными вентилями одной фазы. Если 0^ ^Яг^пс/З, реализуется так называемый дограничный режим работы [37] и происходит чередование интервалов двухфазной (єі) и трехфазной (е2) проводимости (рис. 2.2,а), т. е. тр=єі+Є2. Если я/3<Х<2я/3, осуществляется сверхграничный режим, при котором чередуются интервалы нулевой (е3) и двухфазной проводимости, И Тр—Є3-}-Єі.
Целесообразно ввести в рассмотрение параметр б — угол запаздывания тока в цепях с индуктивной нагрузкой, отсчитываемый от нулевого значения следующей полуволны питающего напряжения (рис. 2.2), и совместить с ним начало расчетного интервала, т. е. то=—jt/2+б. Как видно из рис. 2.2, а=8+А, в догра - ничном режиме Я=єі, и угол проводимости каждого из тиристоров р=л—Я. В сверхграничном режиме кфєі, каждый тиристор коммутирует два импульса тока (Pi и Рг) одинаковой длительности, поэтому p=i(31-f-(32=2pi, Я,=єі+2є3=2тр—Єї.
Определим компоненты матрицы Аг, соответствующие различным схемам включения асинхронной машины.
В режиме трехфазной проводимости (схема ЗФ—С) ias^0,. ibs¥=0, ics¥= 0 и (так как тиристоры каждой фазы проводят ток) UAa=uBb=uCc— 0. Как следует из (2.41) — (2.43), при этих условиях U-00'== 0 и uas—uA, ubs = uB, ucs = uc. Анализ (2.13) и (2.44) для рассматриваемого случая показывает, что Uas — UaN и wps= = wpjv, т. е. вектор напряжения статорных цепей U может быть выражен только через вектор входа JN. Следовательно, при трехфазной проводимости (присвоим матрицам этого режима порядковый номер i=l), как следует из (2.14), Рх = 0 и Bi = Lb Матрицы Bi = Li; Fi = Ri могут быть определены из уравнения (2.8) при записи его в виде (2.10) . Эта матрица, а также Nj приведены в. табл.^2.1. Дву7хфазное включение {схема 2Ф—С) возникает при ^нулевом токе одной из фаз статора. При анализе преобразователя |ЗТТ достаточно рассмотреть эту схему при ias=0 (i=2). Условие
|
Рис. 2.2. Диаграмма фазного напряжения питающей сети (иА) и тока фаз статора (ias, ibs, ics) при управлении от преобразователя по схеме рис. 1.1,а: а — дограиичный режим (по ошибке не показана часть кривой ias до точки Т0); б — сверх - граничный режим |
ias = О ПРИВОДИТ К їа5=0. При *as = 0 И СОк=0, КДК СЛедувТ ИЗ ПЄр-¥
вого уравнения системы (2.8), составляющая напряжения статора!; по оси а равна ЭДС eas, наводимой на обесточенной фазе статора/ (фазе а) электромагнитным полем ротора, т. е. >
Has — Has — & as — L>oDiar' (2-47)
Если /a5=0, то вектор состояния асинхронной машины I описывается ТОЛЬКО тремя компонентами (i$s, іаг, ip г), поэтому квадратные матрицы L, R, Р, В, F при описании этой схемы имеют размер 3X3. Однако по условиям стыковки матричных уравнений необходимо, чтобы указанные матрицы для различных схем включения имели один размер 4X4. Для дополнения матриц до размера 4X4 целесообразно использовать следующий прием: для того чтобы ток в фазе а был равен нулю, необходимо приложить
|
Таблица 2.1. Компоненты матрицы А і для различных схем іключения статорных цепей
со 00 |
к этой фазе напряжение той же величины, что и наведенная в ней (ЭДС, т. е. L0Diar, что и обеспечит исходное условие ias = 0. При таком подходе правые части исходной системы дифференциальных уравнений (2.8) остаются без изменений, в них формально присутствует составляющая ias, поэтому R2 = Rb L2 = Li. При необходимости аналогичный прием будет использоваться и при описании других схем.
В схеме двухфазного включения (ias=0) ивь=иСс=0, поэтому из (2.43) получаем иаъ=иА—иАа, ив0 = ив, ис0 = ис, а из (2.42) следует и00'=—1/3иАа- Подставим эти результаты в первое уравнение системы (2.41). Тогда при Uas — Є as •
u00' = (eas — иа)/2; (2.48)
|
|
|
«С (^as U-д) /2, (wc |
Чbs = U в feas Ид)/2 — (W ЕС
(2.49)
С учетом (2.44) и (2.49) получаем щ8=у1={ив—uc)=u$N.
Приведенные соотношения позволяют определить компоненты матрицы А2 для схемы 2Ф—С (ias=0). Они приведены в табл. 2.1.
При нулевой проводимости фаз статора (0Ф—С) ias — ibs — = ics=0, поэтому t'as=;ps=0. При этом условии
|
<РКг 1 Dv> J |
и _ = LnDi
|
(2.50) |
as
u$s Lfli
т. e. напряжения, приложенные к статору по осям а и р, не связаны с вектором напряжения питающей сети. Для определения матрицы А і (і—3) используем тот же прием, что и при рассмотрении схемы 2Ф—С, поэтому R3 = Ri, L3 = Li. Компоненты матрицы приведены в табл. 2.1.
Зная матрицы Аь А2, А3, можно рассчитать вектор начальных условий V(т0), а затем и вектор состояния V(t). Уравнения, приведенные к виду (2.29), имеют следующие матрицы W, определяемые по (2.30):
для дограничного режима
W = T —eA,<v'V, x; (2.51)
для сверхграничного режима
W - Т — еКг (2тр_Х)^а* (Х_тр) . (2.52)
Подматрица S, входящая в Т, определяется по (2.26) при ок= = 0 и Тр=л/3.
|
w2 |
I Ы |
||
|
W3 |
W4 |
(v> |
Матричное уравнение (2.29) можно записать в виде
где Wi размера 4X4, W2 размера 4X2, W3 размера 2X4, W4 размера 2X2 — подматрицы матрицы W.
Как указано в [30], подматрицы W3 и W4 тождественно равны нулю. Тогда при т0=—зт/2+6 из (2.53) получаем
|
(2.54) (2.54) ; |
Wjl(—3X/2+6)+W2Ujv(—jT/2+б) =0; I (—зт/2+6) = MU* (—я/2+6) ,
|
(2.56) |
где М—матрица размера 4X2,
|
ти |
тп |
|
т21 |
т22 |
|
тй і |
т32 |
|
щ 1 |
т42 |
|
м = —Wr'W2 |
|
(2.57) |
Запишем (2.55) в развернутом виде:
|
las (— */■2 + 8) |
тп |
Щл |
|
|
(— */2 + 8) |
т21 |
||
|
f«r(— 7С/2+ 8) |
т31 |
||
|
*pr (~ w/2 + Щ |
т42 |
|
UaN (~ ,t/2+S); U$N ( 7С/2 “Ь 8)* |
Значение т0 выбиралось из условия, что ias (то)=0, с учетом этого из (2.57) получаем:
0—mnUaN (—зт/2+8) --fti12tipfj (—зт/2+6). (2.58)
Так как иаы{—л/2+8) = cos (—я/2+6), a u$N{—зт/2+8)► = = sin(—л/2+8), то из (2.58) следует
т0=—ji/2+8=arctg(—тп/ти). (2.59)
Таким образом, из (2.59) определено значение то, которое зависит от параметров двигателя, угловой скорости ротора и задаваемого значения Я. Для конкретного типа двигателя при ю= = const значение т0 однозначно связано с параметром Я. При известном То по (2.58) определяются ifiS{ То), *аг(т0), /рг(то), т. е. начальный вектор состояния V(to), а затем и V(t).
При шеститактной симметрии, какой обладает схема ЗТТ, токи и напряжения различных фаз статора и ротора симметричны. В напряжении основной гармоники, которая является полезной составляющей, образующей средний момент двигателя [6], присутствует только система прямой последовательности.
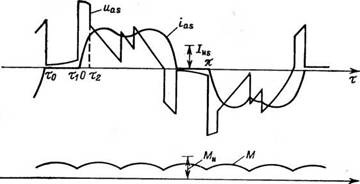
На рис. 2.3 и 2.4 показаны некоторые из рассчитанных с помощью ЦВМ зависимостей, иллюстрирующих работу двигателя МТ012-6 с закороченным ротором при управлении от преобразователя по схеме ЗТТ.
Для наглядности ряд параметров, характеризующих работу двигателя (действующие значения фазных токов и напряжений, средний момент), удобно выражать в других относительных единицах, приняв за базовые величины номинальные значения: для момента Мм, для напряжения U$N (действующее значение номинального фазного напряжения); для токов статора и ротора Isn (действующее значение номинального фазного тока статора). Для новых относительных единиц будем использовать соответствующие буквенные обозначения с индексом звездочка, а для момента введем специальное обозначение:
|
Рис. 2.3. Расчетные осциллограммы напряжения и тока фазы а статора и момента электродвигателя МТ012-6 при фазовом управлении в статорных цепях» схемы рис. 1.1,а; |
|
<0=0,4; а=90°; р,=0,58
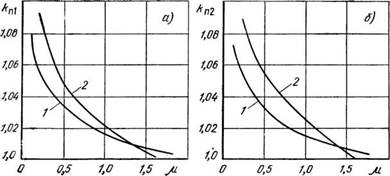
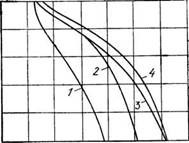
Рис. 2.4. Зависимости kni=f(n) (а), &П2=/(р) (б) для электродвигателя МТ012-6 при фазовом управлении в статорных цепях, схема рис. 1.1,а: / — со=0,2; 2 — <в=0,8 |
Схема ЗТД (см. рис. 1.1,6). В течение периода питающего напряжения включаются три тиристора, фазные напряжения двига-
Рис. 2.5. Расчетные осциллограммы напряжения ито - ка фазы статора и момента электродвигателя МТ012-6 при фазовом управлении в статорных цепях, схема рис. 1.1,6:
|
|
(0=0,4; а=90°; ц=1,24
|
гг |
теля обладают трехфазной симметрией (2.46), поэтому обеспечивается трехтактная симметрия, т. е. g=3, а тР=2я/3 [37], частота пульсаций момента /п= 150 Гц (2.34), токи фаз двигателя симметричны. Как и в схеме ЗТТ, при изменении Я от 0 до тР имеет место дограничный режим (чередование схем включения ЗФ— С и 2Ф—С), а при изменении от тР до 2тр — сверхграничный режим (чередование схем включения 2Ф—С и ОФ—С). Следовательно, для схемы ЗТД справедливы те же расчетные выражения, что и приведенные ранее для схемы ЗТТ, с той лишь разницей, что тр=2я/3. Работу схемы ЗТД иллюстрирует рис. 2.5.
Схема ITT (см. рис. 1.1,г). Предполагается, что тиристоры включены в фазу а статора (см. рис. 2.1). В течение периода питающего напряжения происходит коммутация двух тиристоров через равные интервалы л. Фазные напряжения двигателя удовлетворяют условию полуволновой симметрии (2.45), действующие токи фаз двигателя различны. В схеме преобразователя ITT g= = 2, тР=л, /п = 100 Гц. При изменении % в пределах 0^Х^тР происходит чередование схем включения ЗФ—С и 2Ф—С, следовательно, для определения V(t0) можно использовать (2.51) с учетом того, что подматрица S рассчитывается по (2.26) при тР= =я. Когда Я=тр=зт (чему соответствует а—п), фаза а статора отключена от питающей сети (/as=0), и в течение всего времени работы двигателя реализуется схема включения 2Ф—С. Работу схемы ITT иллюстрируют рис. 2.6, 2.7. Укажем, что на рис. 2.6 заштрихована фигура, площадь которой пропорциональна значению q, определенному по (2.35).
Схема 2ТТ (см. рис. 1.1,в). При рассмотрении схемы 2ТТ предполагаем, что тиристорные элементы включены в фазы а и b статора (см. рис. 2.1). Анализ показывает, что в процессе управления двигателем помимо режима 2Ф—С (ias — 0) возникает еще один вариант двухфазного включения 2Ф—С (ibs=0) [43].
В рассматриваемом случае ibs=0, ias=—ics, ias—Us, i$s= =iaS/y3, uAa = uCc=0, на обесточенной фазе статора наводится ЭДС ebc, т. е. ubc=ebs. Указанные особенности позволяют опреде-
|
(2.61) |
|
|
|
Рис. 2.6. Расчетные осциллограммы напряжений (иа&, иьв, uct) и токов (іав, іь«, іс.) фаз статора и момента электродвигателя МТ012-6 при фазовом управлении в статорных цепях, схема рис. 1.1,г: со=0,4; а=120°; |Л=0,95 |
|
лить составляющие напряжения статора по осям а и р и величину ebs: |
|
(2.60) |
ebs = -0,5L0Diar + V3 L0Dipr[2.
Зная ebs и записав фазные напряжения сети через проекции обобщенного вектора питающего напряжения в соответствии с
(2.5) , определим зависимость U от ІІдг и I, что позволит найти компоненты матрицы At - (і=4) для схемы 2Ф—С {ibs=0). Они приведены в табл. 2.1.
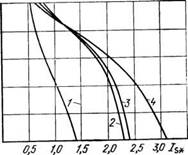
Рис. 2.7. Действующие токи различных фаз статора электродвигателя МТ012-6 при фазовом управлении в статорных цепях, схема рис. 1.1,г, а=90°:
|
|
|
OjB |
|
0,5 1,0 /,5 2,0 2,5 |
/—1 а& 2 — Ibs; 3 — Ig при работе электро - 0,6 двигателя на естественной характеристике;
4 ~ Ofi
Анализ показывает, что из-за полуволновой симметрии фазных токов и напряжений в схеме 2ТТ расчетный период тР=я, а в качестве параметра управления целесообразно выбрать угол а.
Диапазон угла а, обеспечивающий изменение среднего момента от значения на естественной характеристике до нуля, составляет ф^а^7л/6. В зависимости от угла а и скорости возможны четыре режима, отличающиеся на расчетном периоде тР количеством интервалов k, соответствующих различным схемам включения асинхронной машины, и порядком их чередования, на отрезке тР [43]. Режимы I, И, III имеют место при ф<Са<С5я/6, режим IV при 5я/6<а<7я/6. Эти режимы характеризуются следующим значением k и порядком чередования схем включения: режим I, 6 = 4, 2—I—4—1
режим II, k=4, 2—3—4—1
режим III, k=4, 3—2—3—4;
режим IV, k=2, 3—4,
где схемы включения обозначены присвоенными им порядковыми номерами соответственно табл. 2.1.
В схеме 2ТТ на расчетном интервале (тР=я) до нуля падает не только ток ias, но и ток фазы b ibs. Совместим начало расчетного интервала (т=то) с моментом, когда ias=0, и запишем матрицы W (2.29) и М (2.56) для моментов времени, когда ias=О и ibs=0. Обозначим эти матрицы W°, Ма (для тока ias=0) и Wb, Мь (для тока ibs—0) и получим выражения для определения моментов переключения вентилей в различных режимах.
Для режима 1
|
(2.62) (2.63) (2.64) (2.65) (2.66) |
|
22 |
|
где triij |
|
х3 = тс/6-f-a; = 'Ео + 7С> элементы матрицы М (2.56). |
|
т0 = arctg (— mau/mai2); = 7с/2 -{-- OtJ тх — l/З ть2, |
|
г12 — V3 тЬ |
|
х2 = arctg |
Рис. 2.8. Расчетные осциллограммы напряжения (иая, иъе, иС8) и токов (ias, іь«> ісг) фаз статора и момента электродвигателя МТ012-6 при фазовом управлении в статорных цепях, схема рис. 1.1,в:
Ь)=0,4; а=90°; ц.=0,92
Для режима II т0 и Т4 определяются по (2.62) и (2.66):
|
(2.67) (2.68) (2.69) |
г1= arctg (—mzijmw)', Т2 = —я/2+а; Тз=я/6-Ьа.
Для режима III т0, ті и т4 определяются по (2.62), (2.67),
|
(2.70) (2.71) |
Т2= arctg (—/7X21/^22); Тз=—зх/2+а.
Для режима IV то, ті, т2 определяются по (2.62), (2.68), (2.66). Рассмотрим составление алгоритма для расчета на ЦВМ при различных режимах схемы 2ТТ на примере режима I. По (2.62) и
Рис. 2.9. Действующие токи различных фаз статора двигателя МТ012-6 при cj
|
|
фазовом управлении в статорных цепях, схема рис. 1.1,в, а=90°: 0,8
1-Ibs; 2 Ias; 3 — Ict; 4 Is при работе двигателя на естественной характеристике Qfi
0,4
О
(2.65) при заданном а определяются времена п и т3. Принимаются начальные приближения для моментов включения вентилей в фазах а(г0) и Ь(%г). Затем определяются матрицы Wa, Wb, Ma и Мь и уточненные значения т0 и т2 [по (2.62), (2.63)]. Вычисления то и Т2 повторяются несколько раз и заканчиваются при совпадении значений в начале и в конце шага итерации с требуемой точностью. При известном то определяется вектор начальных условий V(to), затем рассчитывается вектор состояния на интервале тР= =п.
По аналогичной методике производится расчет для других режимов.
Поскольку границы между режимами I—III не могут быть выражены в явном виде через исходные параметры, в программе расчета на ЦВМ должен быть предусмотрен последовательный счет, по формулам каждого из указанных режимов, до тех пор пока не найдется решение, удовлетворяющее всем условиям.
Работу схемы 2ТТ иллюстрируют рис. 2.8 и 2.9.