ПОЛУПРОВОДНИКОВЫЙ ЭЛЕКТРОПРИВОД
УПРАВЛЕНИЕ В РОТОРНЫХ ЦЕПЯХ
2.1.2. ФАЗОВОЕ УПРАВЛЕНИЕ
|
|
Из-за мгновенной несимметрии роторных цепей, возникающей при фазовом управлении, примем о)к=*о и обозначим систему координат, вращающихся со скоростью со, через d, q, совместив ось d с фазой а ротора. В этом случае в систему дифференциальных уравнений входят реальные (непреобразованные) значения роторных величин. Связь между проекциями обобщенных векторов ротора (Xdr, xqr) и фазными величинами (хаг, Хы, хсг) выражается, как видно из (2.4), в следующем виде:
(2.79)
|
|
Расчетная схема для систем фазового управления в роторе, показанных на рис. 1.4, приведена на рис. 2.12. При управлении в роторных цепях к статору всегда приложено неизменное напряжение питающей сети, поэтому Uds=UdN, uqs=uqNi а составляющие вектора uN определяются из (2.13) при сок=со с учетом того, что при записи в относительных единицах s=l—to:
(2.80)
Для всех схем фазового управления в роторе матрицы N; •одинаковы и равны матрице Ni, приведенной в табл. 2.1. Матрицы Ні для всех схем также равны друг другу и определяются по (2.18) при сок=о). Главное отличие систем фазового управления в роторе, по сравнению с аналогичными системами в статорных цепях, заключается в том, что период переменного напряжения ти изменяется в зависимости от скорости, т. е. tu=23x/s. Рассмотрим с учетом этой особенности методику определения матриц А і для различных схем включения ротора [47].
|
} |
|
(2.81) |
|
тр =‘tu/g= n/3s> fn — 6f0S. |
|
При анализе схемы ЗТТ в качестве параметра управления выбирается угол 2., который представляет собой интервал между коммутацией тока сопряженными вентилями одной фазы ротора. При работе схемы имеют место два режима: дограничный (O^taOT/З), когда происходит чередование режима трехфаз - ной проводимости ротора (ЗФ—Р), обозначим этот интервал через е2', и двухфазной проводимости (2Ф—Р) — интервал є/; сверхграничный (л;/3<А,^2л/3). В этом случае чередуются режимы 2Ф — Р и ОФ — Р, когда все три фазы ротора обесточены (интервал Єз'). |
Схема ЗТТ (см. рис. 1.4,а). Работа этой схемы аналогична работе схемы ЗТТ в статорных цепях. В течение одного периода напряжения включается шесть тиристоров, токи ротора обладают трехфазной и полуволновой симметрией, поэтому g=6 и
2Ґ
|
|
|
і).., ' |
|
|
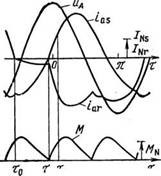
Рис. 2.13. Расчетные осциллограм- ■ jy - мы токов фаз а статора ias, рото-
51 2 pa iar и момента двигателя
~Т I МТ012-6 для фазового управления
І в роторных цепях, схема рис. 1 А, а:
------------------------------ -------------------------------------------------------------- (0=0,4; ц=1,4
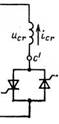
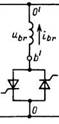
Рис. 2.12. Расчетная схема для систем фазового управления в роторе.
В рассмотрение вводится угол запаздывания тока в фазе а роторной цепи (б), с которым совмещается начало расчетного интервала т0=(—зт/2—{—6)/s.
В рассматриваемом случае составляющие Udr и идг вектора напряжения О не равны нулю при несимметричных схемах включения ротора. Для их определения, как это предложено в [42], будем рассматривать симметричную асинхронную машину, питаемую со стороны ротора от эквивалентного источника с несимметричной системой ЭДС. Тогда по аналогии с несимметрией в статор, ных цепях получаем общие выражения для фазных напряжений ротора (рис. 2.12):
иаг — иа' о и0'0»
иЬг — ub'Q и0'С> (2.82)
Ucr = Ис/0 Uq, q,
где и0,о — напряжение между нулевыми точками обмотки ротора и тиристорного преобразователя.
В рассматриваемой расчетной схеме, так как іаг--іьг--ісг=0, из (2.82) получаем
и0’0 — (иа'о + *Vo + ис'о)/3, (2.83)
Величины иа, о, «ь. о, иСго представляют собой ЭДС, которые, как видно из рис. 2.12, могут быть выражены через падение напряжения на тиристорах, включенных в фазы а, Ь, с ротора (ита, шь, итс), т. е. ^а> “й'О” ‘—
UC'0 ~ ^тс-
При реализации схемы ЗФ — Р все три фазы ротора проводят ток, поэтому Ura = UTb = UTC = 0 И Н0'О=0, следовательно, Uat*=Ubr = Ucr—0 И Uar—Uqr^0. В этой схеме включения (присвоим ее матрицам порядковый номер і—9) Pg=0, Kg=0 и Bg=L9, F9=R9. Матрицы Rg и L9 определяются из уравнения (2.8) при приведении его к виду (2.10) с учетом ТОГО, ЧТО С0к=(0. Полученные компоненты матрицы Ад приведены в табл. 2.2.
Определим матрицу А,- 0=11) для схемы 2Ф — Р, считая, что iar=0. В этом случае (2.79) idr=0, поэтому из третьего уравнения системы (2.8) получаем
tldr==Uarc:=LoDi(is, (2.84)
т. е. в обесточенной фазе ротора наводится ЭДС ear—uar=LoDid8-
В схеме 2Ф — Р (iar = 0) Ujij = итс — 0, ub, Q~uc, Q — 0 и, как следует из <2.83),
а0'0 — иа'0І^~ а/3. (2.85)
Тогда из первого уравнения системы (2.82) получаем
«тс = —1,5 ваг (2.86)
й и0'0 = 0,5
иьг=—0,Ъеаг ^ (2.87)
Пег — 0,5бат- f
Так же как и при рассмотрении схемы 2Ф — С, будем считать, что для выполнения условия idr — 0 необходимо приложить напряжение Udr — edr, оставляя
.неизменным исходные матрицы R и L. Тогда из (2.79) с учетом (2.87) следует,
что u. dr=L0Dids, uqr=0. Матрица Rii = Rg, Lu = Lg. Эти условия позволяют определить компоненты матрицы Ац, приведенные в табл. 2.2.
Рассмотрим схему 0Ф — Р (/=13), когда іаг=іьг=ісг=0. Аналогично схеме 2Ф—Р и в этом случае Ri3=R9, L13=Lg. Напряжения по осям ротора определяются так:
udr = L0Dids; I (
Uqf — L0DlqS. )
Указанные особенности схемы 0Ф — Р позволяют определить компоненты матрицы Аіз, приведенные в табл. 2.2.
В рассматриваемой схеме фазового управления в роторе выражения для W приобретают следующий вид: дограничный режим
у = Т (rt/3—^)/seAii^/s' (2 89)
сверхграничный режим
уу __ 'J'____ —*/3)/s ^2 90)
Подматрица S матрицы Т определяется из (2.26) при {ок=со и tp=3t/3s. Преобразовывая уравнение WV(t)=0 к виду (2.57), определяем, используя условие idr (то) —0, время то и начальный вектор состояния V (т0), а затем по (2.27) и вектор V(t). Таким образом решается задача расчета установившихся режимов при использовании в роторных цепях схемы ЗТТ. Работу этой схемы иллюстрирует рис. 2.13.
Схема ЗТТ с последовательным включением добавочных сопротивлений (см. рис. 1.4,6). Методы расчета этой схемы и схемы ЗТТ (рис. 1.4,а) во всем аналогичны, с той лишь разницей, что при записи матрицы вместо нужно использовать сумму (/?2-М? д)* Матрицы As, Лю, Ai2 приведены в табл. 2.2. Укажем различия в диапазоне регулирования момента этих двух схем. Если в пер
вом случае семейство регулировочных характеристик расположено между естественной характеристикой и осью ординат, то во втором — между искусственной механической характеристикой, соответствующей включению в роторные цепи сопротивления Ra, и осью ординат.
|
'1 ч |
|
Рис. 2.14. Расчетные осциллограммы токов фаз а статора ias, ротора Іат И МОМеНТЭ ДВИ- гателя МТ012-6 для фазового управления в роторных цепях, схема рис. 1.4,в: (0=0,5; Яд=39Я2; |л=0,8 |
|
|
Схема ЗТТ с параллельным подключением добавочных сопротивлений (см. рис. 1.4,в). В этом случае при трехфазной проводимости ротора чередуются три различных схемы включения асинхронной машины. Для двух из них, когда ток проводят тиристоры всех фаз ротора и когда тиристоры всех трех фаз закрыты, матрицы Ад и А8 уже получены.
Рассмотрим схему, когда тиристоры одной из фаз не проводят тока и в нее включено Rn (i= 14). Будем считать, что ток тиристоров фазы а ротора гТОг=0. Тогда в расчетной схеме (см. рис. 2.12) между точками а' и 0 включено Ra и иа, о==—iarRДг. иь о=0, ис'о=0. Как следует из (2.83), и0'0=—iarRJ3.
Тогда из (2.82) получаем:
|
(2.91) |
иаГ ~ 2їаГ/?я/3;
Щг = ‘агЯд/3,
^сг ^аг^д/3-
Значения Udr и идг могут быть определены при подстановке (2.91) в (2.79):
|
(2.92> |
Udr = 2/иГ/?д/3,
uqr = 0.
Как видно из (2.92), в рассматриваемом случае вектор U = = uqs, udr, uqrT зависит от вектора состояния I, а не от его производной, как это было в ранее проанализированных схемах. Поэтому, как следует из (2.14), Кнт^О, Рі4=0. Указанные особенности позволяют определить компоненты матрицы Ah, приведенные в табл. 2.2.
Методика определения вектора начальных условий V(xo) и вектора состояния V (т) полностью аналогична методике, рассмотренной при анализе схемы ЗТТ (см. рис. 1.4,а), с той лишь разницей, что для определения W по (2.89) и (2.90) используются матрицы А8, Ag, Aie.
При работе преобразователя регулировочные механические характеристики заключены между естественной характеристикой и искусственной, соответствующей включению в цепь ротора со
противления Rr. Поэтому Rr должно выбираться таким, чтобы во всем требуемом диапазоне скоростей обеспечить необходимый минимальный момент электродвигателя, что при малых тс приводит к значительным Ra.
Работу этой схемы преобразователя иллюстрирует рис. 2.14.