ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

ДВИЖЕНИЕ МАТЕРИАЛА В ПОПЕРЕЧНОМ СЕЧЕНИИ ТРУБЫ

В настоящее время можно выделить три основных подхода к описанию движения зернистого мате­риала: модель жидкости с особыми свойствами; модель среды, внутреннее трение в которой подчиняет-
ся закону Кулона; так называемый "одночастичный подход", согласно которому движение сыпучего ма­териала рассматривается как осредненное движение отдельных частиц.

В поперечном сечении гладкого вращающегося цилиндра материал можно разделить на два слоя: поднимающийся и скатывающийся. Осевое движение частиц происходит только во время их пребыва­ния в скатывающемся слое, поэтому для расчета трубчатого преобразователя отдельных порций в не­прерывный поток необходимо знать границу раздела слоев.

В работе [23] описан энергетический подход к описанию движения сыпучего материала в попереч­ном сечении гладкого вращающегося барабана. В основу подхода положена гипотеза о постоянстве по­тенциальной энергии, которая сформулирована в следующем виде: при установившемся движении в поле гравитационных сил система достигает такого положения, при котором ее потенциальная энергия равна возможному минимуму, причем достижение указанного состояния происходит путем уменьше­ния массы системы за счет перехода части частиц за границу системы.

Применительно к описанию движения сыпучего материала в поперечном сечении гладкого вра­щающегося цилиндра под системой понимается совокупность частиц, неподвижных относительно обе­чайки цилиндра. На рис. 8.7. показано поперечное сечение гладкого вращающегося цилиндра, частично заполненного зернистым материалом. В поднимающемся слое частицы движутся по концентрическим окружностям с центром на оси вращения и с угловой скоростью, равной скорости вращения цилиндра. Таким образом, частицы, находящиеся

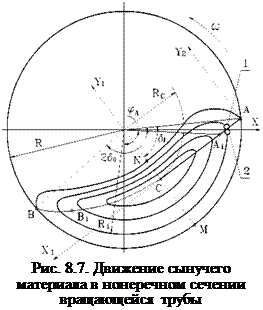в поднимающемся слое, неподвижны относительно цилиндра, поэтому поднимающийся слой часто на­зывают неподвижным слоем. В неподвижном цилиндре весь сыпучий материал входит в систему, а во вращающемся - только частицы, находящиеся в поднимающемся или неподвижном слое.

Поскольку при моделировании процесса преобразования отдельных порций в непрерывный поток будут использованы осредненные параметры движения зернистого материала, энергетический подход представляется наиболее перспективным.

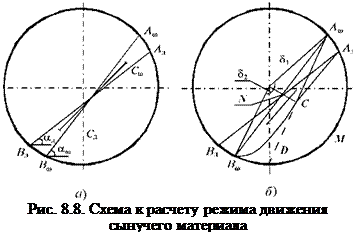
При непрерывном дозировании очень важно знать, в каком режиме движется сыпучий материал. Очевидно, что в режиме периодических обрушений из трубы будет высыпаться не непрерывный поток, а отдельные порции. При достижении открытой поверхностью материала угла осш (рис. 8.8) первона­чально происходит сдвиг материала по линии АтСВт, а затем материал из зоны CNAmAR перемещается в сегмент с открытой поверхностью AjyBjy. Для аналитического описания процесса обрушения сделаны следующие допущения (рис. 8.8, б):

- граница А^СВ^ изначального сдвига сыпучего материала определяется из условия равенства по­тенциальной энергии материала, находящегося в зоне А^СВ^М, минимальной потенциальной энергии системы;

- время перераспределения материала из положения А^В^ в положение Ад Вл равно времени дви­жения частицы из точки Ст в точку Сд{Ст и Сд - центры тяжести соответственно зон ВтАтАлС и ВЛАЛС Вю).

Угол (eta,) наклона открытой поверхности сыпучего материала, при котором происходит переход от состояния покоя к движению, найдем из условия равновесия отдельной частицы [24]:

mgsinoto, - fnmgcosaa -/ao27?(sin50 + fn cos50) = 0 ; (8.12)

аю = arcsin[(co2 R/g) sin(50 + «n)] +«n - (813)

Данная формула наглядно показывает влияние на численное значение угла 0СШ основных режимных и геометрических параметров барабана и свойств зернистого материала: радиуса барабана и угловой скорости его вращения; степени заполнения барабана материалом 8о; угла трения покоя сыпучего мате­риала ап. Из формулы видно, что если сумма углов аш и 8о превышает я/2, то при прочих равных усло­виях численное значение угла 0СШ уменьшается. Данный факт имеет строгое физическое объяснение, по­скольку в рассматриваемом случае точка Ат находится выше горизонтального диаметра и направление центробежной силы пт R не совпадает с направлением силы гравитации.

Далее, используя энергетический подход и зависимости, приведенные в работах [24, 25], определим границу обрушения, т. е. координаты точки С. Координаты центра тяжести зоны В^А^Ац С определим, как координаты сложной фигуры, состоящей из зоны 1 - Bf^NC, ограниченной отрезком параболы СВЮ и пря­мыми BNи NC, и зоны 2 - CNA^Ar - Используя понятие статического момента, координаты центра тяже­сти зоны 1 Хс и Ycі можно найти, используя следующие соотношения:

Xcl = Sxl/Fl, Ycl = Syi/Д, (8.14)

где ^ = j ydF - статический момент зоны 1 относительно оси X, F - площадь зоны 1; Syl = j xdF - стати­ческий момент относительно оси Y.

Аналогично определяются координаты центра тяжести зоны 2:

X2 = S,2/F2, Yc2 = Sy2jf2 . (8.15)

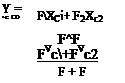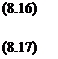Площадь Fa зоны BmAmAaCбудет соответственно равна сумме площадей Д и Д. Координаты точки Сю можно определить, используя следующие зависимости:

Введем следующие обозначения: Д - площадь зоны ЛИШАД; Д - площадь зоны NB^B^ АД, Yc3, АД, УД - координаты соответствующих центров тяжести.

С учетом указанных обозначений

F=F~F+fF,

у F^Xa - F3Yc3+ F4Yc4 Fa-F3+F4

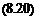Зная координаты точек Ст и Са, несложно найти угол ашд наклона прямой СтСл к горизонту.

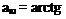
f Y - Y ^

лСО) Ас V _ у

V сю ^сд J

Время тп перемещения центра масс обрушившегося материала из точки Ст в точку Ся определим по следующей формуле:

тп=^ , (8.22)

а

где Аод = - Дд )2 + (■Хм - ^ )2 ] °’5 - длина отрезка Сю Сд;

а = g{sinara - fR cosa0W) - ускорение движения центра масс.

Если численное значение тп больше, чем Хд, то зернистый материал начинает двигаться в циркуля­ционном режиме.

Результаты расчетов и экспериментальные данные [ 19] показали, что предлагаемая методика позво­ляет достаточно точно (с погрешностью не более ±15 %) определить границу перехода от режима пе­риодических обрушений к циркуляционному режиму.

Расчет параметров распределения материалов при циркуляционном режиме движения выполняется в следующей последовательности [19, 24, 25]. При известных значениях R, 5о, осп, осд, fn, /], со по формуле (2.8) находится численное значение угла осш. Далее находятся координаты точек А и В

ХА = 7?sin(ara + 50), Хв= 7?sin(S0 - a J,

^ = -7?cos(ara + 50), YB = -7?cos(50 - аю). (8.23)

Потенциальную энергию материала, находящегося в поднимающемся слое, рассчитывают следую­щим образом:

где F= f(R, со, осп, бо, 8і ) - площадь поднимающегося слоя; у> - расстояние по вертикали от оси враще­ния барабана до центра тяжести сегмента материала, у которого открытая поверхность горизонтальна, т. е. это координата нулевого уровня; L - длина барабана.

Площадь и координаты центра тяжести поднимающегося слоя находят по зависимостям, аналогич­ным (8.14 - 8.20).

Далее рассчитывают численное значение минимальной потенциальной энергии [24]:

Приравняв Пп минимальному значению потенциальной энергии системы, методом последователь­ных приближений находят численное значение угла 6ц Положение центра циркуляции (точка С на рис. 8.7) находят по следующим зависимостям [24]:

(8.26)

Rc = Rcos 5].

Зависимости (8.23, 8.26, 8.27) полностью характеризуют распределение сыпучего материала в попе­речном сечении гладкого вращающегося цилиндра при циркуляционном режиме движения.