Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ

ВЫБОР РЕЖИМА ОБРАБОТКИ, ОБЕСПЕЧИВАЮЩЕГО ЗАДАННУЮ ТОЧНОСТЬ

При проектировании технологических операций, выбирая режим обработки, важно знать ожидаемую погрешность обработки.

Анализ нормативных материалов по выбору режимов резания пока­зывает отсутствие каких-либо данных, указывающих на связь между ре­жимами резания и точностью обработки. Исключение составляет лишь подача, выбор которой связывают с шероховатостью обработанной по­верхности, что явно недостаточно. В итоге выбранные режимы резания не гарантируют получения обработанной детали с заданной точностью, поэтому при выборе режимов приходится их занижать, чтобы гарантиро­вать получение заданной точности, а также затрачивать время на коррек­тировку режимов резания на станке. Все это затрудняет нормирование технологического процесса, не позволяет оптимизировать применяемые решения, препятствует внедрению автоматизации проектирования техно­логических процессов.

Особенно важен выбор режимов резания для станков с ЧПУ при разработке в большом количестве управляющих программ. В связи с от­сутствием возможности рассчитать с требуемой точностью погрешность обработки, вынуждены предусматривать дополнительные проходы, тра­тить время на отладку управляющей программы. В связи с изложенным очевидна необходимость в установлении и математическом описании связей между режимами и точностью обработки. Ниже излагается мето­дика решения задачи выбора элементов режима обработки, обеспечи­вающих заданную точность.

Методика заключается в построении математической модели меха­низма образования погрешностей обработки, назначении по справочно - нормативным данным элементов режима обработки, в получении расче­тов ожидаемой погрешности, сравнении ее значения с допуском и в слу­чае выхода за границы допуска внесения коррективов в режим обработ­ки, обеспечивающих положение погрешности в границах поля допуска.

Рассмотрим пример выбора элементов режима фрезерования, обес­печивающих заданную точность при обработке на вертикально - фрезерном станке мод. 6Р12, предназначенном для фрезерования плоско­стей, различного рода пазов, канавок и т. п. Для решения этой задачи по­строим математическую модель механизма образования погрешностей обработки.

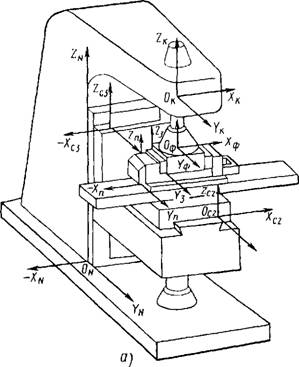
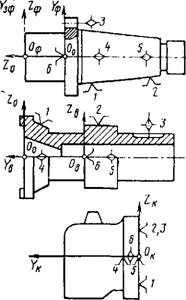
На рис. 1.9.1, а показан вертикально-фрезерный станок, где замы­кающим звеном при фрезеровании является расстояние между режущими кромками фрезы и установочной базой заготовки. На рис. 1.9.1, в, г при­ведены детали, входящие своими размерами в размерную цепь станка, на которых в соответствии со схемой их базирования построены координат­ные системы.

При условии, что фрезерование осуществляется за счет продольного движения стола, среди деталей, входящих в размерную цепь, шпиндель и продольный стол имеют по одной степени свободы. Шпиндель вращает­ся, а стол совершает поступательно-возвратное движение.

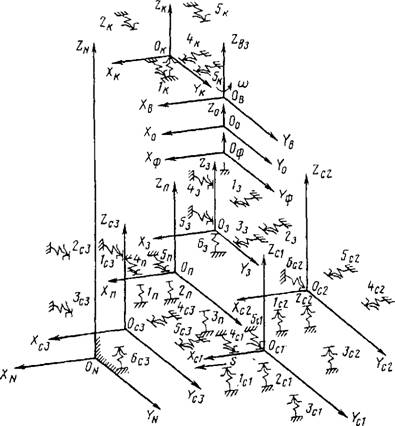
После построения координатных систем на основных базах деталей (для заготовки основные базы совпадают с технологическими) и, исклю­чив детали, получим эквивалентную схему, приведенную на рис. 1.9.1, б. В качестве неподвижной системы координат XiV, в которой осуществляются все перемещения остальных координатных систем, принята система, постро­енная на вертикальных направляющих (вспомогательных базах) стойки станка. Пользуясь полученной эквивалентной схемой (см. рис. 1.9.1, б), за­пишем уравнение относительного движения вершины зуба фрезы в системе координат Z„ построенной на технологических базах заготовки.

Пусть фреза совершает вращательное движение по закону u> u>U). а стол движется поступательно по закону s = s(t), тогда

+ МвМшМкг0 + МШМКГЪ - Мс]Мс2Мс, гс] + -

~ Mc}?ci - Mc]Mc2Mc3sx +rK-rN],

І де R ф - радиус-вектор, определяющий положение вершины зуба фрезы в координатной системе заготовки; М~3,М~2, Л/',1 - обратные матрицы

0)

Рнс. 1.9Л (продолжение)

Поворотов координатных систем деталей, входящих в ветвь заготовки; Мш - матрица поворота координатной системы шпинделя по закону ш = ш(/); Sx - вектор перемещения координатной системы стола про­дольной подачи по закону s = s{t)\ ..., А/к - матрицы поворотов коор­динатных систем деталей ветви инструмента под действием внешних

* ^ ^ \°п

Осі

Za

-0сг

Осі

"сг

Рис. 1.9.1 (окончание)

Факторов; - радиус-векторы, соединяющие начата координаї

Ных систем деталей ветви инструмента; Мс), ..., A/t3 - матрицы поворотон координатных систем деталей ветви заготовки под действием внешних факторов; - радиус-векторы, соединяющие начата координат

Ных систем деталей ветви заготовки.

Введем в уравнение движения факторы, порождающие погрешность обработки. В связи с этим рассмотрим, прежде всего, силы, действующие непосредственно во время фрезерования. К этим силам относятся силы резания, тяжести, инерции, а также крутящий момент, передаваемый на фрезу, и подача, передаваемая столу посредством кинематики станка. Чтобы ввести эти силы и моменты в модель, надо знать, в каких коорди натных системах они действуют, а также точки их приложения, направ ления действия и их величины.

Силы резания действуют одновременно на заготовку и фрезу, по этому рассматривают их действие в координатных системах фрезы 1ф и заготовки

В процессе фрезерования в зависимости от положения заготовки на столе, конфигурации обрабатываемой поверхности, числа зубьев на фре­зе будут изменяться точка приложения, направление и величина равно­действующей сил резания, действующих на зубьях фрезы. Поэтому, что бы определить перечисленные выше переменные, необходимо устано­вить соответствующие зависимости. В основу этих зависимостей поло­жен угол контакта <рк, определяющий число одновременно работающих зубьев фрезы, однако угол контакта может изменяться из-за переменной ширины фрезерования. Сложность установления зависимости, опреде­ляющей число одновременно работающих зубьев, объясняется случай­ным характером изменения ширины фрезерования от одного типа заго­товки к другому.

Ширина фрезерования есть функция конфигурации заготовки, ее ус­тановки на столе станка и относительного расположения фрезы и заго­товки. Определив положение заготовки в координатной системе стола станка, контур обрабатываемой поверхности разбивают на участки, кото­рые могут быть описаны соответствующими уравнениями.

Следующим шагом является определение координат точек контакта фрезы с линиями контура обрабатываемой поверхности заготовки. Дтя этого достаточно решить систему уравнений, включающую уравнение данного участка контура обрабатываемой поверхности и уравнение ок­ружности диаметром, равным диаметру фрезы.

Зная угол ф3 между зубьями фрезы и угол контакта фк фрезы с заго­товкой, можно рассчитать число одновременно работающих зубьев из формулы Z3 = фк/ф,. Если это отношение дробное, то число зубьев в рабо­те за один оборот фрезы будет изменяться на единицу. Зная число одно­временно работающих зубьев, легко подсчитать величину равнодейст­вующей сил резания, ее направление и координаты точки приложения.

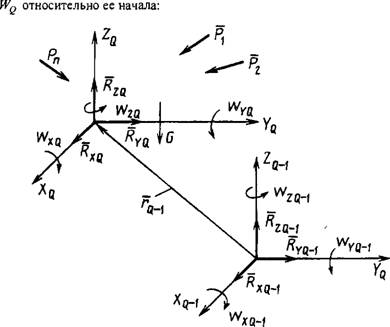
Найдем реакции в каждой опорной точке каждой координатной сис­темы эквивалентной схемы. Пусть на Q-ю координатную систему экви­валентной схемы действуют внешние силы, Рп - система сил реза­ния на каждом зубе фрезы, находящемся в фиксированный момент вре­мени в зоне резания; G - масса детали, на которой построена Q-я коорди­натная система (рис. 1.9.2).

Чтобы найти реакции в опорных точках Q-й координатной системы, определим главный вектор Rq и главный момент системы внешних сил

Rq = RxQ + Rya + R:o; wq = WxQ + WyQ + W:Q;

N n

RxQ = + Gxo' Wxq = ^(PyZ, - P. jXJ) + GxQZ(J - G. JJXQ ;

7=1

^.vo = S Рм + GyQ; ^Vj = X _ РчУ))+ GXJxC> - Cvo-Vcj;

= + w*i = £( V; - V/) + ЈWo-GyoZg,

7 = 1 7 = 1

Где z; - координаты точек приложения внешних сил; PXJ, Pyj, P:J проекции внешних сил на координатные оси j-й координатной системы. Rxq, RyQ, R:q - проекции главного вектора на оси координатной системы Wxq, W:(j - проекции вектора главного момента на оси координатной системы.

Составим систему уравнений равновесия статики:

Где NI(JI, Ny(jn N:Qi - реакции j-й опорной точки Q-й координатной систе мы по направлениям X, У, Z; х^, уц, z- координаты j-й опорной точки Q-й координатной системы.

Решение системы уравнений относительно реакций Nt„ NVI, N-, по­зволит определить искомые реакции в опорных точках Q-й координатной системы.

Для того чтобы перейти к расчету реакций в следующей координат­ной системе необходимо: предварительно определить перемещения опорных точек, положение Q-й координатной системы относительно {Q - 1)-й координатной системы, сформировать матрицу Nq поворота Q-й координатной системы; определить главный момент И/(;_1 и главный

Вектор R0_x внешних сил относительно начала (Q - 1)-й координатной системы по формулам:

^х(о-і) = MQWxQ + MQ{RxQzQ_{ - R! QxQ-\)\ Wy(Q-\) = MQWyQ + MQ{RyQxQ_x - Rxgyo-0;

1) = MQWzQ + MQ{R, QyQ^ - RyyZg-i),

Где Mq - матрица поворота Q-й координатной системы под действием внешних сил; уц-ь zy_t - координата начала Q-й координатной сис­темы в координатной системе Q - 1с учетом перемещений начала Q-й координатной системы под действием внешних сил и моментов.

Расчет реакций для (Q - 1)-й координатной системы проводится аналогичным образом, как и для Q-й координатной системы по уравне­нию равновесия статики: в котором значения Rx(j, Rylj, R:(J, Wx<), W„> заменяются значениями RX(ij-\), R-xo-\ И^у-п. И^у-n - Зная реакции и жесткости в опорных точках, можно рассчитать упругие перемещения по­следних; жесткости в опорных точках определяются экспериментально.

Чтобы ввести в модель изнашивание и геометрические погрешности направляющих стола и шпинделя, устанавливают зависимость между износом и отклонением геометрии направляющих, а затем между откло­нениями геометрии направляющих и перемещениями опорных точек в соответствии с методикой, приведенной в п. 1.8.3.

Ниже приводится пример расчета погрешности фрезерования с по­мощью полученной модели.

Исходные данные сведем к четырем группам.

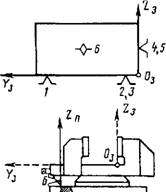
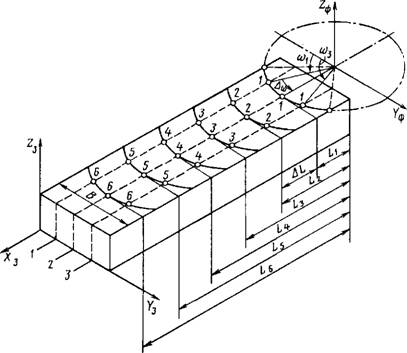
• 1. Данные, определяющие условия обработки: глубина резания, минутная подача, частота вращения шпинделя, диаметр фрезы, число зубьев фрезы, геометрия заточки, стойкость фрезы, материал заготовки, материал режущего инструмента, твердость материала заготовки, ширин. і фрезерования В по сечениям заготовки и расстояния L, до сечений ш торца заготовки со стороны входа фрезы в зону резания (рис. 1.9.3).

• 2. Данные, характеризующие технологическую систему: жесткое 11, в опорных точках, координаты опорных точек элементов технологиче­ской системы, координаты начал координатных систем этих элементов и количество элементов.

• 3. Система ограничений, налагаемых на технологическую систем\ допустимые значения составляющих сил резания; мощность; скорость ш> стойкости режущего инструмента; значение подачи, ограниченной тре бованиями шероховатости поверхности.

• 4. Точностные и размерные параметры заготовки: допуск на обра ботку, заданный размер детали.

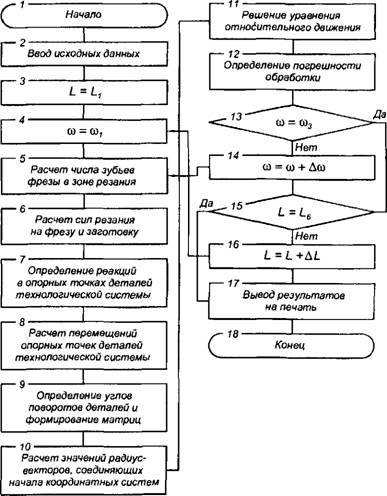
Пусть на станке обрабатывается заготовка призматической формы (см. рис. 1.9.3). Расчет погрешности фрезерования проводился в соответ­ствии с алгоритмом, показанным на рис. 1.9.4. Погрешности рассчитыва­лись в 18 точках, расположенных в трех продольных и шести поперечных сечениях.

После ввода исходных данных (блок 2) переменной L присваивается значение L\ (блок 3), т. е. заготовка выводится в заданное сечение. Затем фреза поворачивается на угол Ш) таким образом, чтобы зуб фрезы со вместился с первой точкой первого сечения заготовки, и переменной (II присваивается значение сої (блок 4). Определяется число зубьев фрезы, находящихся в зоне резания (блок 5). Это позволяет рассчитать силы ре зания, действующие на фрезу и заготовку (блок 6) и приступить к расчет \ перемещений и поворотов координатных систем эквивалентной схемы.

Расчеты ведутся в следующем порядке: определяются реакции в опорных точках деталей технологической системы (блок 7); рассчитыва­ются перемещения опорных точек деталей технологической системі, I (блок 5); определяются углы поворотов координатных систем и форми руются матрицы поворотов (блок 9); определяются значения ради>с векторов, соединяющих начала координатных систем (блок /0); по уран нению относительного движения рассчитывается значение радиус вектора, определяющего положение вершины зуба фрезы в заданной том ке обработанной поверхности (блок //) при наличии упругих перемете ний; определяются погрешности обработки в заданной точке (блок 12) как разница между заданным значением радиус-вектора и расчетным значением.

Если переменная ш = со3 (блок 13), т. е. определена погрешность в за данных точках сечения, то переходят к следующему сечению заготовки (блок 15). Если переменная изФ ш3 (блок 13), то фреза поворачивается на угол Дш, переменной со присваивается значение со + Дсо (блок 14) и расче­ты повторяются с блока J.

Если условие блока 15 выполняется, т. е. рассмотрены все сечения заготовки, расчеты заканчиваются выводом на печать погрешности обра ботки в заданных точках заготовки. Если условие блока 15 не выполняет ся, заготовка перемещается на величину AL (ДL = L, - /-,_)) и переменной L присваивается значение (1( - U. О и расчеты повторяются с блока 4 В табл. 1.9.1 показаны варьируемые параметры.

На основании приведенного алгоритма была разработана программа для расчетов на ЭВМ. По результатам расчета во всех точках всех сече ний погрешность обработки колебалась от 0,015 мм до 0,214 мм. Макси­мальное расхождение измеренной погрешности обработки с расчетным значением получилось в точке 1 (см. рис. 1.9.3) первого сечения и соста­вило 0,02 мм при погрешности обработки 0,214 мм, а расчетной - 0,194 мм С помощью данной программы определяются значения элементов режи ма фрезерования, обеспечивающие заданную точность обработки.

Определив по справочникам рекомендуемые для заданных условий обработки элементы режима фрезерования, рассчитывается погрешность

Фрезерования АЛ = Лф - Л в каждой точке полученной поверхности. Ес­ли окажется, что AR > Т, где Т - допуск на отклонение R, то необходи­мо внести коррективы в значения одного из элементов режима фрезеро­вания (как правило, в продольную подачу).

С этой целью расчеты погрешности повторяют с меньшим значени­ем величины 5М, и ее величина уменьшается до тех пор, пока не будет

Достигнуто равенство AR = Т.

Более сложно решается задача назначения режимов при многоинст - рументной обработке. Например, на практике выбор режимов резания для многорезцовой обработки производится следующим образом.

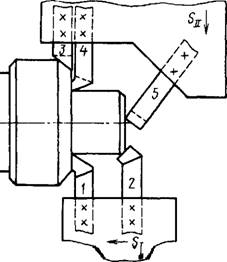
По составу и числу инструментов, требованиям к точности обработ­ки, по виду обработки назначаются ориентировочные значения подач суппортов (см. рис. 1.9.5). Затем находят экономичные стойкости инст­рументов при их изолированной работе. Найденные по экономичным стойкости и подаче экономичные скорости резания корректируются с

Учетом кинематической связанности подач и скоростей резания на от­дельных инструментах. Такая методика имеет следующие недостатки нет гарантии получения заданной точности обработки; не учитывается взаимное влияние факторов, действующих на разных резцах, на погрет ности обработки каждой поверхности.

Отмеченные недостатки методики присущи не только для одно шпиндельных многорезцовых токарных станков, но и для других станков многоинструментной обработки.

По данным многочисленных исследований, доминирующим факто ром в образовании погрешностей при многорезцовой обработке являются упругие перемещения, что объясняется обработкой заготовки одноврс менно несколькими резцами и недостаточной жесткостью станка.

Изменение условий обработки на одном из резцов влечет за собой и общем случае не только количественное, но и качественное изменение характера процесса образования погрешности на поверхностях, обраба тываемых другими резцами. Эта взаимосвязь обусловлена сложным хл рактером упругих перемещений общих звеньев технологической системі.! под действием постоянно изменяющихся сил резания и их моментов действующих на разных резцах в течение обработки. Поэтому влияние н.< ючпость обработки изменения режимов резания на отдельных инстру­ментах необходимо рассматривать как функцию от комплекса условий оОработки на других инструментах.

Для решения такой задачи тоже методом координатных систем с деформирующими связями строится математическая модель механизма образования погрешностей многоинструментной обработки, посредством ко юрой с помощью ЭВМ устанавливаются зависимости между погреш­ностями обработки от каждого обрабатывающего инструмента и режи­мами обработки. С помощью этих зависимостей можно определить ре - жимі.1, обеспечивающие заданную точность.