Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ

Методы достижения точности замыкающего звена

Графически размерная цепь представляет собой замкнутый контур размеров, из чего следует, что величина замыкающего звена является функцией составляющих звеньев:

Лд=/(ЛЬЛ2, ... Ат. О,

Где Лд - замыкающее звено; А, - составляющее звено; т - число звеньев в размерной цепи.

Из схемы плоской размерной цепи с параллельными звеньями (рис. 1.3.21) видно, что номинальное значение замыкающего звена Лд равно алгебраической сумме номинальных значений составляющих звеньев:

A& = - Ai +А2 + А3-А4,

В которой увеличивающие звенья имеют знак "+", а уменьшающие - знак "-"; увеличивающее звено указывается стрелкой, направленной вправо, а уменьшающее звено - стрелкой, направленной влево. Тогда

А& = - Л, + А2 + Аъ - Д,.

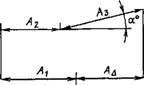
Если плоская размерная цепь содержит звено Аъ распложенное под углом а к направлению замыкающего звена (рис. 1.3.22), то оно вклю­чится в размерную цепь своей проекцией на направление замыкающего звена, по­этому его отклонение скажется в мень­шей степени на величине замыкающего звена.

В связи с этим был введен коэффи­циент, названный передаточным отноше­нием £,. Тогда в общем виде уравнение плоской размерной цепи можно записать как алгебраическую сумму произведе­ний:

M-1

A^Y^aA (1.3.1) 1=1

Или

И m-1

(1-3.2)

/=1 «+1

Іде ї — 1,2 ... порядковый номер составляющего звена; т - число звеньев размерной цепи; - передаточное отношение г-го составляющего зве­на (для плоских размерных цепей с параллельными звеньями = 1 - для увеличивающих составляющих звеньев и = -1 - для уменьшающих составляющих звеньев).

В процессе изготовления деталей и сборки изделий действуют мно­гочисленные факторы, вызывающие погрешности размеров, в результате чего всегда фактическое значение звена размерной цепи отклоняется от его номинального значения.

Говоря о погрешностях звеньев, следует различать погрешности од­ного изделия и погрешности группы изделий:

- для одного изделия погрешности звеньев имеют определенные значения и направление в сторону уменьшения или увеличения фактиче­ского значения размера от номинального;

- для группы изделий под погрешностью звена понимается поле рассеяния погрешностей ш.

Учитывая изложенное, звено размерной цепи (рис. 1.3.23) в общем случае будет характеризоваться номинальным значением Лном, полем рас­сеяния, координатой поля рассеяния Лш.

Что касается конкретного значения звена размерной цепи одного из­делия, то его величина Л,- будет лежать в пределах границ поля рассеяния.

Конструктор при разработке чертежей деталей, понимая неизбеж­ность наличия погрешностей размеров, назначает на каждый размер со­ответствующий допуск Г, ограничивающий погрешность. В этом случае вместо со и Аа пользуются полем допуска и координатой середины поля допуска До.

Чтобы получить годное изделие, надо, чтобы в результате его изго­товления должно быть обеспечено ш < Т.

Номинальные размеры и координаты середин полей допусков име­ют знаки и потому суммируются ал­гебраически, а допуски и поля рассея-

TOC \o "1-3" \h \z ния не имеют знака и поэтому сумми - а

Руются арифметически.

Отсюда следует, что для расчета д

Плоской размерной цепи с параллель - ------- ^

Ными звеньями необходимо решить три L-------------------------- І----------------------- »

Уравнения: номинальных размеров, ко­ординат середин полей рассеяния (до - Рис> 1>3>23. Схема характеристик

Пусков) и полей рассеяния (допусков).

Так, например, для разм^РН0Й цепи, приведенной на рис. 1.3.21: уравнение номинальных размер06

Лд = --Д +А2+А3-А4;

Уравнение полей допусков

Тлй=Тм+ТА2+ТАі+ТАі,

Где ТА& - допуск замыкающего звена; Тл. - допуск г'-го составляющего звена;

Уравнение координат середин нолей допусков

Л0АЛ = - Л0; 1 +Л0^2 + А0Л3 ~ЛСМ4>

Где Дол - координата середины поля допуска замыкающего звена; Аоа, - координата середины пс, ля допуска г-го составляющего звена. В общем случае имеем:

Т-1

= (1.3.3)

1-І

Таким образом, поле допу°ка замыкающего звена плоской размер­ной цепи с параллельными звеньями равно сумме абсолютных значе­ний полей допусков всех составляющих звеньев:

П т-1

A0A=ЈSAw-ZsA/ (1.3.4)

,=1 л+1

ИЛИ

Т-1

До> = Е5А»- (1.3.5)

I=i

При расчете величины Aoz, надо учитывать не только знаки Д0/,но и знаки их составляющих звенья

Пусть имеем - Д01,-Д02, Д<м ■ Тогда с учетом знаков состав­ляющих звеньев-Ль Аг, As,-A будем иметь

Д<М4 = "(Лол,)+ (~л0>12) + СДохз) - (А<м4 ) ■

Таким образом, координаты середины поля допуска замыкающего зиена плоской размерной цепи с параллельными звеньями равна алгеб­раической сумме координат середин полей допусков составляющих звеньев с учетом знаков составляющих звеньев.

Формула, учитывающая связь поля рассеяния значений замыкающе­го звена (его отклонений) с полями рассеяния значений составляющих звеньев (их отклонений), может быть получена путем аналогичных рас­суждений. Не прибегая к ним, приведем формулу в общем виде:

M-1

Юд = 1|ф,; (1.3.6)

1=1

Для плоских размерных цепей с параллельными звеньями

/и-1

Шд=2>«- (1.3.7)

(=1

Все рассуждения, касающиеся координат середин полей допусков, в полной мере распространяются и на координаты середин полей рассея­ния. Поэтому по аналогии будем иметь

И m-1

ДЮД=ХАш,.-1Аш, (1.3.8)

/«і «

Или

/и-1

Дшд. = ^Ао,- (1.3.9)

/=1

При расчетах допусков и полей рассеяния звеньев размерных цепей существует два принципиально разных подхода:

- расчет на максимум-минимум;

- вероятностный расчет.

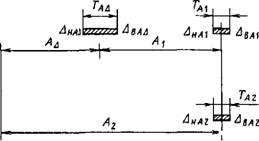
Метод расчета на максимум-минимум учитывает только предель­ные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания. Например, в размерной цепи А, показанной на рис. 1.3.24, А\ = - А\ + Ai. Предельные отклонения замыкающего звена будут при следующих сочетаниях предельных отклонений составляющих звеньев:

ДвЛд +Дв/1Д2; ДнЛд = ""^М, +

Вычитая почленно из первого равенства второе, получим

К*, - ЛнЛ, М-ЛнЛ, - AHaJ-

Разность верхнего и нижнего предельных отклонений есть поле до­пуска, в пределах которого допустимы отклонения звена, поэтому

Таь=ТАі+ТА2.

Вероятностный метод расчета учитывает рассеяние размеров и ве­роятность различных сочетаний отклонений составляющих звеньев раз­мерной цепи. Теоретическую основу для установления связи между по­лем допуска замыкающего звена и полями допусков составляющих звеньев размерной цепи составляют положения теории вероятностей. В связи с этим будем рассматривать замыкающее звено у как функцию случайных аргументов xt.

На основании теории вероятностей можно утверждать, что среднее значение будет функцией средних значений аргументов:

Y=f(xu х2, ... х„).

Для ограничения рассеяния случайных отклонений функции и аргу­ментов полями допусков воспользуемся формулой об их дисперсиях, ко­торую в данном случае удобнее представить в виде зависимости средних квадратических отклонений:

А* < + 2^(ду/дх^Хду/дх^Сх. а^^.

І=І j*i

Рассматривая составляющие звенья размерной цепи как независи­мые величины и принимая отсутствие корреляционной связи между до­пусками на составляющие звенья, можно воспользоваться зависимостью

А2у=^(ду/дх,)2х1а2хг /=1

При теоретических расчетах полем допуска Т ограничивается рас­сеяние случайных отклонений, распределенных по нормальному закону, в пределах бст. Поэтому

Где кх - коэффициент, учитывающий закон распределения отклонений аргументов через коэффициент Хх. и принятый процент риска, обуслав­ливающий выход значений функции у за пределы усатновленного допус­ка кх. = Хх ; здесь t - коэффициент риска.

Отсюда

Где /д - коэффициент риска, характеризующий процент выхода значений замыкающего звена за пределы установленного на него допуска: X, - ко­эффициент, характеризующий выбираемый теоретический закон рассея­ния значений г'-го составляющего звена.

Возможное поле рассеяния замыкающего звена при известных полях рассеяния составляющих звеньев можно рассчитать по формуле

FfM

GSft2,»?- (1.3.11)

В плоских размерных цепях, имеющих звенья, расположенные под углом к выбранному направлению, каждое из таких звеньев можно заме­нить его проекцией на это направление. Тем самым любую плоскую раз­мерную цепь можно привести к размерной цепи с параллельно располо­женными звеньями.

В качестве примера на рис. 1.3.22 приведена размерная цепь А, в ко­торой звено А з находится под углом а относительно направления замы­кающего звена ВА. Замыкающее звено этой размерной цепи

Аь = - А\ + А2 +Аз cos а - Л4.

Как отмечалось, пространственная размерная цепь - это цепь, у ко­торой имеются звенья, расположенные под углом в двух координатных плоскостях. При расчете таких размерных цепей они рассматриваются в трех координатных плоскостях и используют проекции ее звеньев на три направления:

Аи = Ai cos а,;

Aty = A, cos Р,;

Alz = AjCOsXi,

Где Aix, Aiy, Aiz - проекции А-го звена на соответствующие координатные оси; aj; Р/, Xj - углы между А,-м звеном и направлением соответствую­щей координатной оси.

Тригонометрические функции, используемые для получения проек­ций звеньев на соответствующие направления, выполняют в данном слу­чае роль передаточных отношений, учитывающих одновременно принад­лежность звена к числу увеличивающих или уменьшающих звеньев. По­этому формулы (1.3.1), (1.3.3), (1.3.5) можно использовать и при расчете размерных цепей со звеньями, повернутыми относительно направления замыкающего звена.

Прямая и обратная задачи. При расчете размерных цепей все за­дачи сводятся к решению прямой или обратной задачи.

При решении прямой задачи исходными данными являются номи­нальный размер замыкающего звена, его допуск и координата середины поля допуска. В результате расчетов должны быть найдены значения но­минальных размеров, их допусков и координат середин полей допусков всех составляющих звеньев размерной цепи.

Прямая задача, как правило, решается конструктором на этапе про­ектирования изделия. При этом рассчитываются только поля допусков и координаты середин полей допусков. Что касается номинальных раз­меров, то они уже определены конструкцией изделия, поэтому применя­ется проверочный расчет, чтобы определить правильность номинальных размеров.

Решение прямой задачи является неопределенным, так как число неизвестных и в уравнении допусков, и в уравнении координат середин нолей допусков равно т - 1, а для их расчета имеется по одному уравне­нию (1.3.3) и (1.3.5), что заставляет прибегать к различным способам ре­шения. Одним из таких способов является решение прямой задачи с ис­пользованием коэффициентов сложности достижения точности состав­ляющих звеньев.

Коэффициент сложности по своему физическому смыслу выражает возможность достижения уровня точности размера в нормальных произ­водственных условиях без дополнительных затрат и учитывает: трудно­сти обработки поверхности, достижимый уровень точности на оборудо­вании в исправном состоянии, размер и др.

С помощью коэффициентов сложности определяются допуски на все составляющие звенья, кроме одного, а затем решается уравнение до­пусков относительно оставшегося составляющего звена.

Например, пусть размерная цепь содержит четыре составляющих звена А\, А2, Аз, А4; в исходных данных задан Тл замыкающего звена.

Сначала с помощью коэффициентов сложности определяются до­пуски Т{, Тг и Тъ. Затем записывается уравнение допусков, где неизвест­ным будет допуск на звено Л4, т. е.

Т4 = Тд-(Т\+ Т2 + Тз).

Аналогично определяются координаты середин полей допусков. Пользуясь системой допусков и посадок, определяются предельные от­клонения координаты середины полей допусков всех составляющих звнеьев, кроме того же составляющего звена. Затем записывается уравне­ние середин координат полей допусков относительно координаты сере­дины поля допуска этого звена и, таким образом, рассчитывается ее зна­чение.

Другой способ решения прямой задачи заключается в том, что снача­ла принимается условие равного влияния допусков всех составляющих звеньев на величину замыкающего звена, т. е. на все составляющие звенья назначается один и тот же допуск, найденный путем деления допуска замыкающего звена на число составляющих звеньев. После этого с уче­том коэффициентов сложности корректируются допуски на все состав­ляющие звенья, кроме одного. Затем, записав уравнение допусков отно­сительно допуска оставшегося составляющего звена, находят его значение.

Аналогично рассчитывают координаты середины полей допусков на составляющие звенья.

При решении обратной задачи, исходя из значгний номинальных размеров, полей допусков, координат середин полей допусков, предель­ных отклонений составляющих звеньев, определяют те же характеристи­ки замыкающего звена (в данном случае решением обратной задачи про­веряют правильность решения прямой задачи). Если необходимо опреде­лить ожидаемую точность замыкающего звена, находят поле рассеяния, координату его середины или границы отклонений замыкающего звена на основании аналогичных данных о составляющих звеньях.

Задача достижения точности замыкающего звена размерной цепи в зависимости от допуска замыкающего звена, конструкции изделия, усло­вий производства может решаться одним из пяти следующих методов: полной взаимозаменяемости, неполной взаимозаменяемости, групповой взаимозаменяемости, регулировки и пригонки.

Метод полной взаимозаменяемости. Сущность его заключается в том, что требуемая точность замыкающего звена размерной цепи у любо­го экземпляра изделия достигается при включении в нее или замене в ней любого составляющего звена без выбора, подбора или изменений их ве­личин (например, при сборке 100 соединений «вал-втулка» необходимо обеспечить в каждом соединении заданную величину шора; при методе полной взаимозаменяемости заданный зазор получится при соединении любой втулки из ста с любым валом).

Простейшим примером применения метода полной взаимозаменяемости яв­ляется соединение электрической лампы с патроном. Купленная в любом магази­не лампа всегда ввернется в любой патрон.

Основными преимуществами метода полной взаимозаменяемости являются:

1) простота достижения требуемой точности замыкающего звена. Например, использование этого метода при сборке превращает послед­нюю в простое соединение деталей;

2) простота нормирования процессов во времени, при помощи ко­торых достигается требуемая точность замыкающего звена;

3) возможность широкого использования основных преимуществ кооперирования различных цехов и отдельных заводов для изготовления отдельных деталей или сборочных единиц машин (ларикороликовых подшипников, электроаппаратуры, гидронасосов, агрегатных узлов стан­ков, автомобильных моторов и т. д.);

4) возможность выполнения технологических процессов рабочими, не обладающими высокой квалификацией.

Недостаток метода полной взаимозаменяемости сэстоит в том, что допуски на составляющие звенья назначают исходя и$ обеспечения за­данной точности замыкающего звена при условии сочетания в размерной цепи составляющих звеньев с крайними значениями.

Например, зазор в соединении « вал-втулка » будет обеспечен, когда диа­метр вала будет максимальным в пределах допуска, а диаметр отверстия во втул­ке будет минимальным, или наоборот, диаметр вала будет минимальным, а диа­метр отверстия во втулке будет максимальным.

Однако на практике вероятность сочетания всех составляющих звеньев с крайними значениями в одном изделии невелика, даже в таком простом соединении как "вал-втулка". И чем больше звеньев в размерной цепи, тем меньше вероятность сочетания в одном экземпляре изделия всех составляющих звеньев с крайними значениями. Отсюда следует вы­вод о том, что применение метода полной взаимозаменяемости приводит к ужесточению допусков на составляющие звенья. При этом ужесточение допусков при одном и том же допуске на замыкающее звено тем выше, чем больше составляющих звеньев. Это следует из формулы расчета ве­личины среднего допуска:

Тср=ТА/(т-1). (1.3.12)

Поэтому экономически целесообразной областью использования метода полной взаимозаменяемости являются малозвенные размерные цепи и размерные цепи со сравнительно широким полем допуска замы­кающего звена.

Метод неполной взаимозаменяемости. Сущность его заключается в том, что заданная точность замыкающего звена при получении размер­ной цепи путем включения в нее или замене в ней любого звена без вы­бора, подбора или изменения их величины достигается не во всех экзем­плярах изделия.

Отличие рассматриваемого метода от предыдущего заключается в установлении больших по величине допусков на составляющие звенья, что делает изготовление деталей и эксплуатацию машин, которым при­надлежат эти звенья, более экономичными. Однако при этом идут на риск получения некоторой доли случаев выхода погрешности замыкаю­щего звена размерной цепи за пределы установленного допуска.

В основе рассматриваемого метода лежит одно из известных поло­жений теории вероятностей, по которому возможные сочетания крайних значений погрешностей всех составляющих размерную цепь звеньев встречаются несравненно реже, чем средних значений. Вследствие этого при значительном расширении допусков составляющих звеньев процент изделий, имеющих выход погрешностей замыкающего звена за пределы требуемого допуска, будет небольшим.

Изложенное можно проиллюстрировать на примере трехзвениой размерной цепи Ал = А\ - А2. Для упрощения задачи допуски составляю­щих звеньев взяты равными, т. е. ТА] = ТАг. Примем, что для обоих со­ставляющих звеньев рассеяние их значений подчиняется закону нор­мального распределения (закону рассеяния Гаусса). Как известно, при этом условии рассеяние значений замыкающего звена также будет Гаус­совым, так как

Если для решения задачи использовать метод полной взаимозаме­няемости, то при требуемом допуске замыкающего звена ТА допуск ка­ждого из составляющих звеньев

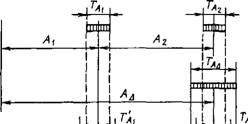
Изложенное схематически показано на рис. 1.3.25. При решении этой же задачи методом неполной взаимозаменяемости допуски обоих со­ставляющих звеньев, как указано выше, устанавливаются большими, т. е

Т'л, > ТА{ и ҐАі > ТАі.

Соответственно и допуск замыкающего звена в этом случае будет больше, чем необходимо, на величину

Где Т'А = - Т'А, как это показано на рис. 1.3.25.

Это обстоятельство может вызвать появление некоторой части изде­лий с погрешностью замыкающего звена, выходящей за пределы требуе­мого допуска ТА замыкающего звена. Величина этой части изделий оп­ределяется отношением суммы двух заштрихованных площадок а и б (рис. 1.3.25) ко всей площади кривой рассеяния замыкающего звена.

Преимущества метода неполной взаимозаменяемости заключаются в том, что задаваясь небольшой величиной риска выхода значений замы­кающего звена за пределы допуска, можно существенно расширить до­пуски составляющих звеньев по сравнению с допусками, назначенными по методу полной взаимозаменяемости.

Таким образом, метод неполной взаимозаменяемости не гарантирует получения 100 % изделий с отклонениями замыкающего звена в пределах заданного допуска. Однако дополнительные затраты труда и средств на исправление небольшого числа изделий, размеры которых вышли за пре­делы допуска, в большинстве случаев малы по сравнению с экономией труда и средств, получаемых при изготовлении изделия, размеры деталей которого имеют более широкие допуски. При сборке изделий дополни­тельные затраты труда и средств вызываются разборкой изделий с откло­нениями замыкающего звена, выходящими за пределы допуска, и воз­вращением их деталей в тары в расчете на то, что в сочетании с другими деталями эти детали окажутся пригодными для других экземпляров со­бираемых изделий.

Экономический эффект, получаемый от использования метода не­полной взаимозаменяемости вместо метода полной взаимозаменяемости, возрастает по мере повышения требований к точности замыкающего зве­на и увеличения числа составляющих звеньев в размерной цепи.

Метод групповой взаимозаменяемости. Сущность метода заклю­чается в том, что требуемая точность замыкающего звена достигается путем включения в размерную цепь составляющих звеньев, принадлежа­щих к одной из групп, на которые они предварительно рассортированы.

При применении метода групповой взаимозаменяемости поле до­пуска Гд замыкающего звена, заданное условиями задачи, увеличивается в целое число п раз для получения экономически эффективного допуска. Расширенное таким образом поле допуска, часто называемое производст­венным допуском Гд=«Гд, используют для расчета допусков состав­ляющих звеньев размерной цепи. Детали, изготовленные по таким более широким допускам, в сравнении с методом полной или неполной взаимо­заменяемости, сортируют на п групп. Изделия собирают из деталей, при­надлежащих только одной из групп, что позволяет достигать точности замыкающего звена в пределах заданного допуска Гд

Таким образом, при сборке изделий из деталей одной группы точ­ность замыкающего звена достигается методом полной взаимозаменяе­мости.

В качестве примера достижения точности замыкающего звена мето­дом групповой взаимозаменяемости вернемся к соединению "вал - втулка". Зная величину допуска ТАд на зазор Ал, расширяют его в п раз, тогда и допуски на составляющие звенья тоже расширятся в п раз. После изготовления валов и втулок их сортируют на п групп и каждой группе присваивается номер.

После изготовления валов и втулок их сортируют по указанным группам и затем собирают вал со втулкой одной группы. В итоге все со­единения получаются с зазором в пределах Гд. Таким образом, примене­ние метода групповой взаимозаменяемости позволяет достигать заданной точности замыкающего звена при экономически выгодных допусках на составляющие звенья.

Этот метод также применяют в случаях, когда имеющееся оборудо­вание не может обеспечить заданную точность деталей, рассчитанную методом неполной взаимозаменяемости.

Однако следует иметь в виду, что применение метода групповой взаимозаменяемости связано с дополнительными затратами труда на сор­тировку деталей, их клеймение, хранение; в результате усложняется ор­ганизация производства.

С увеличением числа групп эти расходы увеличиваются и при ка­ком-то числе групп потери эффективности производства превысят поло­жительный эффект. Увеличиваются дополнительные расходы и с увели­
чением числа звеньев в размерной цепи. Поэтому применение метода групповой взаимозаменяемости нашло при достижении точности замы­кающего звена у малозвенных размерных цепей.

На практике метод групповой взаимозаменяемости нашел примене­ние для таких изделий, как шарико - и роликоподшипники, соединения пальцев и поршней двигателей и др., где число звеньев в размерной цепи не превышает четырех.

Использование метода групповой взаимозаменяемости требует очень четкой организации измерения, сортировки, хранения, транспорти­рования и сборки деталей. Малейшая путаница в виде попадания деталей из одной группы в другую исключает возможность получения требуемой точности. Поэтому все рассортированные по группам детали обычно маркируются условными знаками или раскладываются в специальную тару для хранения и перевозки.

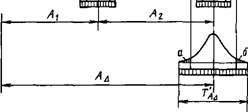
Метод пригонки. Сущность метода заключается в том, что тре­буемая точность замыкающего звена размерной цепи достигается изме­нением размера компенсирующего звена путем удаления с него опреде­ленного слоя материала. На рис. 1.3.11 (с. 58) показан пример размер­ной цепи, где точность Ад достигается за счет съема припуска кольца с размером Аъ.

При достижении точности замыкающего звена методом пригонки на все составляющие звенья размерной цепи устанавливают целесообразно достижимые (экономичные) в данных производственных условиях вели­чины допусков:

71Г Til rpt

1, If, ..., lm

Если с такими допусками изготовить детали размерной цепи, то по­грешность на замыкающем звене выйдет за рамки заданного допуска Гд, так как

Избыток погрешности на замыкающем звене, наибольшее значение которого называют наибольшей расчетной величиной компенсации 5К = Гд >ГД, должен быть удален из размерной цепи путем изменения значения заранее выбранного звена, выступающего в роли компенсатора.

При выборе в размерной цепи компенсатора руководствуются сле­дующими соображениями:

- в качестве компенсатора выби­рают деталь, изменение размера (яв­ляющегося одним из составляющих звеньев) которой при дополнительной обработке требует наименьших затрат;

- недопустимо в качестве компен­сатора выбирать деталь, размер кото­рой является общим составляющим звеном параллельно связанных размер­ных цепей. Нарушение этого условия приводит к возникновению погрешно­сти, "блуждающей" из одной размерной

Цепи в другую. Например, если избрать компенсирующим звеном А2 = Б2 в параллельно связанных размерных Цепях (рис. 1.3.26), то, добившись требуемой точности Аа за счет изменения значения Л2, уже нельзя изме­нять значение Б2, не нарушая точности А&.

Основным преимуществом метода пригонки является возможность изготовления деталей с экономичными для данных производственных условий допусками. При этом точность замыкающего звена оказывается независимой от точности деталей, она определяется точностью выполне­ния пригоночных работ и используемых средств контроля. Методом при­гонки может быть обеспечена высока^ точность замыкающего звена.

Однако пригоночные работы г основном выполняют вручную и тре­буют высококвалифицированного тр/Да. Сложность пригоночных работ заключается в том, что в их ходе необходимо в комплексе обеспечить точность формы, относительного поворота дополнительно обрабатывае­мых поверхностей деталей и расстояния между ними. Упущение одного из показателей точности обычно приводит к потере качества изделия.

Существенным недостатком метода пригонки являются значитель­ные колебания затрат времени при выполнении операции пригонки из-за колебания величины компенсации 5К. Это затрудняет нормирование при­гоночных работ и выполнение сборка с установленным тактом. По этой причине пригонку не рекомендуется применять при изготовлении изде­лий поточными методом.

Экономичной областью использования метода пригонки считается мелкосерийное и единичное производство, хотя не редки случаи, когда метод пригонки из-за своих высоких точностных возможностей оказыва­ется единственно пригодным для обеспечения требуемой точности изде­лий, производимых в значительных количествах.

Метод регулировки. Сущность ме­тода заключается в том, что требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена без удаления материала с компенсатора.

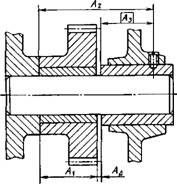
Метод по своей сути не отличается от метода пригонки. Разница заключает­ся лишь в том, что компенсация погреш­ности на замыкающем звене осуществля­ется изменением положения компенси­рующего звена или его заменой на звено с другим размером. В первом случае компенсатор называют подвижным, во втором - неподвижным. Примером под­вижного компенсатора может быть втул­ка в редукторе (рис. 1.3.27), перемещая которую в осевом направлении можно регулировать зазор Ад между ее торцом и торцом зубчатого колеса, сидящего на валу. После достижения требуе­мой точности зазора положение втулки фиксируют стопорным винтом.

Роль подвижных компенсаторов в машинах могут исполнять специ­альные устройства, зачастую автоматические.

В качестве неподвижных компенсаторов используют проставочные кольца, прокладки и другие детали несложной конструкции. Если для достижения требуемой точности замыкающего звена Ад в конструкции, приведенной на рис. 1.3.11, применить метод регулирования, то в качест­ве неподвижного компенсатора целесообразно использовать проставоч - ное кольцо (звено Аз). Для подбора компенсатора нужного размера зара­нее изготавливается группа компенсаторов разных размеров. Обеспече­ние требуемой точности зазора Ад в этом случае сводится к измерению расстояния между торцами зубчатого колеса и бобышки корпуса в пред­варительно собранном устройстве, к выбору компенсатора надлежащего размера и установке его в устройство при окончательной сборке.

Для метода регулировки характерны следующие преимущества:

1) возможность достижения высокой точности замыкающего звена в многозвенных размерных цепях с экономичными допусками на состав­ляющие звенья;

2) меньшие затраты времени на регулировочные работы по сравне­нию с пригоночными работами;

3) простота нормирования и организации сборочных работ по срав­нению с методом пригонки;

4) возможность автоматического восстановления точности замы­кающего звена в процессе эксплуатации изделия.

К недостатку метода регулировки следует отнести необходимость в ряде случаев изменения конструкции изделия путем ввода специальной детали, выступающей в роли компенсатора.