Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ
Геометрическая точность детали и изделия
В общем случае под точностью понимается степень приближения фактического значения параметра к заданному значению.
Между геометрической точностью изделия и выполнением им служебного назначения имеют место качественные и количественные связи. Рассмотрим их на конкретных примерах.
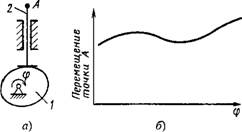
Пример 1. Кулачковая пара (рис. 1.2.7). С ее помощью заготовка подается в рабочую зону станка-автомата в заданный момент времени. И соответствии с этой задачей определяется необходимый профиль кулачка /, обеспечивающий при равномерном вращении требуемую закономерность возвратно-поступательного движения толкателя 2. Вследствие отклонения фактического профиля кулачка от заданного, наличия зазора между осью и отверстием в кулачке 1, а также смещения центра отверстия кулачка 1 относительно заданного положения, фактическая траектория движения толкателя 2 будет отличаться от теоретической. В итоге шготовка будет подана в другую точку рабочей зоны из-за опоздания или опережения. Это может вызвать или поломку станка-автомата, так как поступающая заготовка может столкнуться с предыдущей, или потерю производительности вследствие запаздывания поступления заготовки.
|
Рис. 1.2.7. Влияние погрешности кулачка на перемещение толкателя: Ч кулачковая пара: 1 - кулачок; 2 - толкатель; б - график перемещения точки А |
|
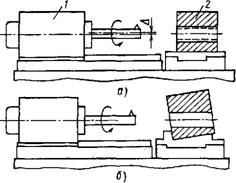
Рис. 1.2.8. Схема растачивания отверстия: А - при несовпадении осей оправки и шпинделя; б - в результате погрешности установки заготовки; 1 - шпиндельная бабка; 2 - заготовка (штриховой линией показано заданное отверстие; сплошной линией - отверстие, полученное после обработки); Д - несовпадение осей шпинделя и расточной оправки |
Пример 2. Расточной станок. При растачивании отверстия в заготовке на расточном станке требуется обеспечить заданную точность диаметра, формы отверстия и положения оси отверстия (рис. 1.2.8). Из-за несовпадения оси оправки с осью шпинделя (рис. 1.2.8, а) возникает погрешность диаметра, из-за погрешности положения установочной базы приспособления (рис. 1.2.8, б) возникает отклонение оси обрабатываемого отверстия от заданного положения.
Геометрическая точность изделия есть функция геометрической точности его деталей.
Геометрическая точность детали. Под геометрической точностью детали понимается степень приближения реальной детали к ее геометрическому прототипу. Точность детали определяется измерением ее погрешности (под погрешностью детали понимается степень отличия реальной детали от ее геометрического прототипа).
Оценка точности детали осуществляется с помощью ряда показателей. Для оценки погрешности надо сопоставить реальный контур детали с контуром ее прототипа. Для этого необходимо относительно контура прототипа записать измеренный контур реальной детали. Если деталь больших размеров, то обеспечить это физически затруднительно из-за потребности в большой площади. Кроме того, при высоких требованиях к шчности потребуется дополнительно увеличить размеры контура, что приведет к еще большим размерам. При расположении контура детали оиюсительно контура прототипа возникает многовариантность решения ной задачи, а отсюда и неоднозначность в оценке погрешности.
В итоге пошли по пути оценки точности детали с помощью группы показателей точности. Поскольку деталь представляет собой совокупность элементарных поверхностей, то условились оценивать точность ас і ал и через точность ее поверхностей и их относительного положения.
Точность поверхности определяется точностью ее размеров и геометрической формы.
Размер понимается как расстояние между двумя небольшими участками двух или одной поверхности, поэтому практически в подавляющем (юлі. шинстве случаев безразлично, от которой из двух поверхностей или in какой из выбранных частей одной поверхности до другой производит - I я измерение расстояния. В соответствии с этим размер принято изображать двусторонней стрелкой, соединяющей участки измеряемых поверхностей или одной поверхности.
Точность геометрической формы поверхности описывается с помощью грех показателей точности: макрогеометрии, волнистости и микро - I еометрии:
1) под макрогеометрическими отклонениями понимают отклонения реальной поверхности от правильной геометрической формы в пределах габаритных размеров этой поверхности (например, отклонение плоской поверхности от плоскостности, поверхности кругового цилиндра, конуса, шара от их геометрических прототипов);
2) под волнистостью понимают периодические неровности поверхности, встречающиеся на участках протяженностью от 1 до 10 мм;
3) под микрогеометрическими отклонениями (микронеровностями) понимают отклонения реальной поверхности в пределах небольших ее участков, обычно размером 1мм2 (микрогеометрические отклонения начинают шероховатостью поверхности).
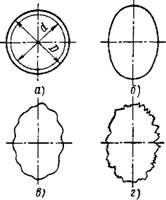
В качестве примера на рис. 1.2.9 показаны отклонения сечения ци - нипдрической поверхности детали:
Отклонение диаметрального размера Ad=D - d (рис. 1.2.9, а)\
- макрогеометрическое отклонение, когда вместо окружности профиль реальной поверхности является овалом (рис. 1.2.9, б); волнистость (рис. 1.2.9, в); шероховатость (рис. 1.2.9, г).
Рис. 1.2.9. Погрешности детали:
А - погрешность диаметра; б - погрешность формы; в - волнистость; г - шероховатость
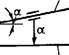
. Точность относительного положения поверхностей детали в плоскости принято оценивать с помощью расстояния и поворота (рис. 1.2.10), где положение плоскости А относи-
Тельно плоскости Б оценивается с помощью размера а и угла поворота а.
Недостаток дифференциального метода оценки точности детали заключается в необходимости установления связей между всеми показателями точности.
|
|
Между показателями точности детали существуют качественные и количественные взаимосвязи. Пока можно говорить только о качественных связях, так как функциональных зависимостей, существующих между перечисленными показателями точности детали, до сих пор в общем виде не установлено. Не зная микроотклонений, трудно говорить о точности формы (в смысле макрогеометрических отклонений), так как при измерении макроотклонений в измеренную величину в качестве одного из слагаемых войдут микронеровности, если не будет предпринято специальных мер для исключения их влияния (например, при измерении погрешности макроотклонений от вершины гребешков микронеровно-
|
А |
|
Б Рис. 1.2.10. Показатели точности относительного положения поверхностей А и £ детали |
|
О |
Стей используют измерительный инструмент с наконечниками, перекрывающими несколько гребешков, и пренебрегают при этом величиной смятия гребешков в процессе измерения).
Не зная макроотклонений поверхности, также трудно судить об отклонениях поворота одной по-
Ш-рхности относительно другой, так как при измерении этого отклонения макроотклонения будут влиять на величину измеренного отклонения. 11ри некоторых же формах макроотклонений поверхности практически не представляется возможности даже измерить отклонение поворота одной поверхности относительно другой без введения особых условий и специ - аш. пых методов измерения (например, относительно выпуклой поверхности А (рис. 1.2.11, а) нельзя определить, насколько она отклоняется от параллельности к поверхности Б, если даже последняя представляет со - (>ой плоскость).
Если отклонение от параллельности измерять, например, с помощью уровня, то при его непосредственной установке на отдельные участки выпуклой поверхности А остается неизвестным, какую величину его отклонения и на каком участке измеряемой поверхности считать за отклонение от параллельности.
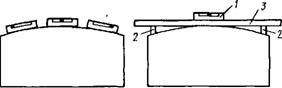
Только установив по краям измеряемой поверхности детали две калиброванные плитки 1,2 и наложив уровень на поставленную на них линейку 3, можно условно говорить об отклонении этой поверхности от параллельности второй поверхности, посредством которой деталь установлена на контрольной плите (рис. 1.2.11,6).
Трудно также говорить о точности расстояния между двумя поверхностями, так как на измеренное отклонение оказывают влияние отклонения поворота поверхности, макро - и микроотклонения.
Из изложенного следует:
1) измерение точности детали должно начинаться с измерения мик - ронсровностей, затем должны измеряться макронеровности, далее отклонения поворота поверхности и, наконец, точность расстояния или размера;
|
0) б) Рис. 1.2.11. Влияние погрешности формы поверхности на отклонение от параллельности: А - влияние на измерение отклонения от параллельности положения уровня; б- измерение отклонения от параллельности с помощью линейки; 1 - уровень, 2 - калиброванные плитки; 3 - линейка |
2) допуски на расстояния и размеры поверхностей детали должны быть больше допусков на величину отклонений поворота поверхностей, которые, в свою очередь, должны быть больше допусков на макрогео - метрические отклонения, а последние больше допусков на микрогеометрические отклонения.
После изготовления деталь подлежит контролю, по результатам которого устанавливается соответствие ее геометрических погрешностей допускам.
Геометрическая точность конструкции изделия. Изделие выполняет свое служебное назначение посредством относительного движения или положения исполнительных поверхностей, поэтому под геометрической точностью изделия понимается степень соответствия фактической траектории относительного движения или положения исполнительных поверхностей заданному движению или положению, которые являются функцией точности деталей изделия.
Рассмотренные выше показатели, характеризующие точность детали, целиком используются и для характеристики точности изделия. Различие заключается только в том, что у детали все показатели точности относятся к поверхностям только данной детали, у изделия же они относятся к исполнительным поверхностям, принадлежащим различным деталям изделия.
Если точность деталей влияет на точность относительного движения или положения исполнительных поверхностей изделия, то геометрическая точность конструкции всего изделия или его механизмов влияет на качество выполнения им служебного назначения.
Исходя из изложенного выше, точность изделия характеризуется следующими основными показателями:
1) точностью относительного движения исполнительных поверхностей изделия;
2) точностью расстояний между исполнительными поверхностями или заменяющими их сочетаниями поверхностей и размеров;
3) точностью относительных поворотов исполнительных поверхностей;
4) точностью геометрических форм исполнительных поверхностей;
5) шероховатостью исполнительных поверхностей.