Оптоэлектроника

Вероятности переходов и осцилляции Раби

Как мы видели в разделе 1.6 в двухуровневой системе синусоидальное возмущение с частотой со вызывает переходы между двумя уровнями с вероятностью:

• пропорциональной /2, если переход имеет монохроматический и резонансный характер (т. е. если квант возбуждения Ь со равен энергетическому зазору между двумя уровнями Е2 - Е{);

• пропорциональной /, если возбуждение носит полихроматический характер, или если конечное состояние принадлежит континууму.

Эти результаты выглядят несколько абсурдными, так как они приводят к расхо­димости в пределе при больших значениях 7. Такое поведение естественно недопу­стимо, так как величина вероятности не может превысить единицу. В дальнейшем мы покажем, что матрица плотности предлагает другое модельное описание систе­мы, которое способно примирить эти трудности.

В первом приближении предположим, что времена релаксации заселенности и фазы (соответственно Тх и Т2) бесконечны, т. е. что системы не подвержены слу­чайным флуктуациям или демпфированию. В этом случае уравнение (1.100) может быть записано в виде:

-^-Ар = -2£1п{р2Х - рп)со$Ш (1Д1 а)

Ш

^-р2х =-<ъ1Хр2,-'£1пАро, оъШ (1.Д.16)

Ш

6

— рх2 = Ш2хр[2 + £1х2Ар СОБ Ш (1.Д-1*)

Ш

Где Дресть различие заселенности рп ~р22, при этом частота Ц2 дается соотношением:

Тп = Ш12 (1.Д.2)

Ожидая резонансный и колебательный характер вблизи <у21, введем частотную отстройку 6со

Дсо = со-со2х (1-Д-З)

Кроме того, введем новые переменные:

О 21 = (1.Д.4я)

0,2 = р12е-*«>.' (1.Д.4 б)

Подставляя эти новые переменные в (1.Д.1) и оставляя только члены с (ква - зи-резонансное приближение), получаем:

= -1пх2(<у2хе'*»‘ - <7,2е-^') (1.Д.5я)

(1.Д.56)

Ш 2

-тт°12 = (1.Д.5е)

А/ 2

Оптические бяоховские уравнения

Уравнения (1.Д.5я) — (1.Д.5<?) называются блоховскими уравнениями. Они мо­гут быть решены с использованием пробных функций:

Ар = Ар°сл‘ (1-Д-6д)

О 21 = о^е-1&"ед' (1.Д.66)

О,, = о102е+1&'е'1' (1.Д.6»)

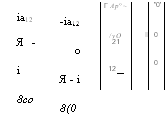
Подставляя (1.Д.6я) — (1.Д.6<?) в (1.Д.5я)—(1.Д.5<?), легко получаем систему уравне­ний в новой форме:

Я *^12 2 -

(1Д.7)

Для получения нетривиальных решений детерминант уравнения (1.Д.7) должен быть равен нулю. Таким образом, мы имеем только три возможные значения:

Я = О, А = П, Л = -.

Где О, — частота Раби, определяемая соотношением:

О, = д/(я> - (о2Х У + 0.}2

Теперь, мы можем определить поведение элементов матрицы плотности в функ­ции времени. В главе 3 мы возвратимся к вопросу о значении недиагональных эле­ментов ап и (т21, обеспечивающих базис для описания эффектов поглощения. Сейчас же нас интересуют вероятности переходов, т. е. диагональные элементы рп и р22.

Предположим, что в момент времени / = О система находится в основном со­стоянии |1), т. е. что:

Р\ — Р22 * О

(1.Д.9)

Ґт 0 — ітО = Г)

12 12 и

Вероятность того, что система занимает первое возбужденное состояние |2) в функции времени дается соотношением:

(1.Д. Ю)

Ш

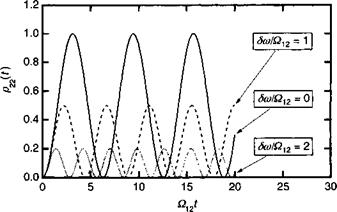
Рисунок 1 .Д. 1 иллюстрирует зависимость этой вероятности от соотношения 8со/0,п.

Из представленного рисунка видно, что вероятность осциллирует с часто­той О, и что амплитуда осцилляций достигает максимума и равна 1, когда 8ю— О (т. е. когда возбуждение резонансно по отношению к энергетическому зазору между двумя уровнями). В этом случае (1.Д.10) дает:

Л2(')=5ІП:

Для коротких промежутков времени (П12 / < 1) вероятность заселенности при­обретает вид:

(1.Д.12)

Это соотношение представляет из себя ничто другое, как уравнение (1.79), по­лученное с использованием зависящей от времени теории возмущений. Как это можно увидеть из рисунка 1.Д.1 синусоидальная функция для коротких промежут­ков времени обладает выраженным параболическим характером. Соответственно формализм матрицы плотности отражает этот параболический характер для малых значений /, накладывает предел применимости и предсказывает осциллирующий характер в течение протяженных периодов времени. Такой долговременный осцил-

1. Д. Вероятности переходов и осцилляции Раби 57

Лирующий характер вероятности заселенности наблюдался в атомах и называется осцилляциями Раби.

Попытаемся теперь описать систему, изменяющуюся под воздействием влия­ния релаксационных механизмов. Уравнение (1.101) может быть записано в виде:

-j-Ар = -1Ю. п(р2[ - рХ2)cos cot —

D t

^р2і = - ісо2Хр2Х - і£212Др cos М-£я-

— px2 = iщ{рп + iЈ2Ap cos cot - Ј&-

D' T2 (1.Д.13в)

Где Ap — различие заселенности pn — p22 и A/?eq есть различие заселенности в состо­янии термодинамического равновесия. Этот подход идентичен использованному в уравнении (1.Д.1) за исключением того, что уравнения становятся существенно более сложными. Ограничиваясь случаем резонанса и полагая 5со =0 и Т2 = Тх = у~ нам удастся сохранить используемые выражения в сравнительно простом виде. Прини­мая в качестве начальных условия, содержащиеся в (1.Д.9), мы получаем:

(1.Д.14)

Где в данном случае Я дается соотношением:

(1.Д.15)

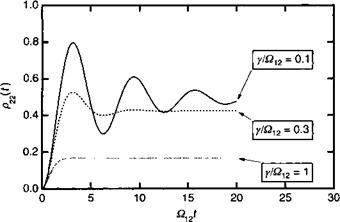
Указанная зависимость иллюстрируется рисунком 1.Д.2.

Отметим, что после переходного периода система испытывает затухание (т. е., теряется когерентность между состояниями |1) и |2), при этом сохраняется стацио­нарная вероятность нахождения системы в возбужденном состоянии, которая дает­ся соотношением:

In*

2 “12

Й?2 + 2 у2

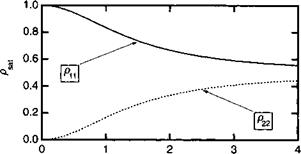
Рисунок 1.Д. З иллюстрирует зависимость заселенности /?8ШП и рвХя122 от амплиту­ды связи 0,12.

Заметим, что в зависимостях заселенности проявляется тенденция к выравни­ванию уровня до значения 1/2 по мере увеличения амплитуды связи. Интерпрета­ция этого механизма, называемого оптическим насыщением, будет дана позже с ис­пользованием корпускулярной теории света Эйнштейна при обсуждении наведен­ного и стимулированного излучения.

Проведенный анализ позволяет в полной мере оценить гибкость и силу форма­лизма матрицы плотности при описании нестационарного характера когерентных оптических переходов, а также при корпускулярной трактовке механизмов перехода.

QJY

Рис. 1.Д. З. Зависимость стационарных заселенностей двух уровней от соотношения частоты Раби и скорости затухания.