Валентные подзоны
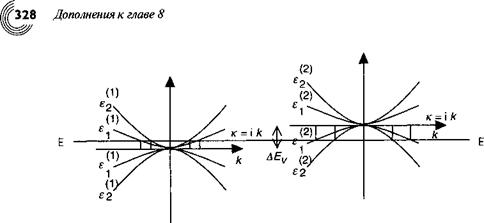
В разделе 8.3 мы уже видели, каким образом электронное ограничение потенциалом ямы приводит к сдвигу минимума зоны проводимости и проявлению квантовой энергии ограничения. В случае валентной зоны мы уже не можем использовать ту же аппроксимацию. Уровни у потолка валентной зоны являются вырожденными по отношению к подзонам легких и тяжелых дырок в центре зоны Бриллюэна. В дополнении 1.Б мы уже видели, что возмущение может приводить к снятию выврождения уровней. И в этом случае мы смогли решить задачу, устано
вив векторное подпространство, перекрываемое вырожденными состояниями, а также изучая влияние возмущения на это подпространство. Сейчас мы покажем, каким образом можно расширить этот подход с тем, чтобы включить в него аппроксимацию огибающей функции для набора зон.
Основной идеей, лежащей в основе этой аппроксимации, является предположение о том, что волновые функции дырок могут быть представлены в виде ряда:
Здесь: ип0 есть волновые функции в центре зоны Бриллюэна для различных дырочных подзон (т. е. п = 1 для тяжелых дырок и п = 2 для легких дырок), а £п есть огибающая функция, которая изменяется в пределах существенно большего масштаба длин по сравнению с постоянной решетки. При рассмотрении в пределах многих элементарных ячеек уравнение (8.Г.1) показывает, что мы находимся в векторном подпространстве, образованном вырожденными дырочными зонами. Уравнение Шредингера для у всегда может быть выражено в виде:
|
(8.Г.2) |
![]() _£_+Кс(г) + К(г) у{т)=Еу,(г)
_£_+Кс(г) + К(г) у{т)=Еу,(г)
Здесь К есть кристаллический потенциал, а У есть внешний потенциал. Это уравнение можно записать также и в виде:
|
(РС,)[Р«„о(г)] Та |
![]()
|
= £^«„0(г)С(г) (8.Г. З) |
![]() У «.«(Г) ^- + е., + К(г) Ш +
У «.«(Г) ^- + е., + К(г) Ш +
П _2т°
Здесь мы использовали тот факт, что ип0 представляют собой стационарные состояния кристалла при к = 0 с энергией ем. Подобно тому, как это уже неоднократно делалось на протяжении этой главы, спроецируем это уравнение на известный базис. Для этого умножим это уравнение на м*0 и проинтегрируем по всему пространству. Изменение £п в пределах постоянной решетки пренебрежимо мало, поэтому мы можем привести интегралы к более удобному виду, следуя методу, использованному в (8.55). Ортогональность блоховских функций в пределах каждой ячейки приводит к следующему уравнению для £п:
|
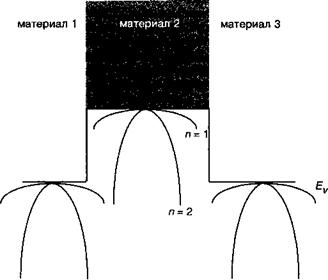
Рис. 8.Г.1. Валентные зоны в квантовой яме. |
|
<Г*(г) + [р<Г„(г)1 = (Е - eN0){N(T) |
|
+ y^(*a<.v, 4" «о |
|
П2 |
|
■+v{z) |
|
2 тп dz |
|
Рт + У г? то |
|
+/?'2)е^г) Az |
|
2т0 |
|
7Ef-fe> |
|
1 Nn Mt, |
|
+ Г(г) |
|
2/и„ |
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|
|
|
|
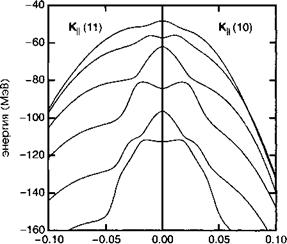
К„ (А'1) |
Рис. 8.Г. З. Валентные подзоны квантовой ямы, соответствующие движению, параллельному границам раздела, являются непараболическими. В данных рас - счетах предполагалось, что ширина ям составляет 12 нм, глубина — 44 мэВ, а высота барьеров — 70 мэВ.
В каждом материале. Четыре соотношения (8.Г.8)—(8.Г.9) для УУ= 1 (тяжелые дырки) и ТУ = 2 (легкие дырки) определяют четыре коэффициента для материала квантовой ямы в функции двух коэффициентов в материале барьера при I > £/2. Граничные условия на границе раздела при г+ = £/2 определяют четыре коэффициента для затухающих волн в материале барьера. В этом случае мы должны искать энергии и коэффициенты ау устраняющие коэффициенты ап0). После этого нам остается только определить нормировочный коэффициент для волновой функции.
Хотя методология расчета и ясна, сами расчеты должны проводиться численными методами. Некоторые из иллюстрирующих примеров приведены на рис. 8.Г. З. Очевидно (что и не удивительно), что дисперсионные кривые каждой подзоны значительно отклоняются от простых парабол.