Оптические переходы между валентной зоной и зоной проводимости
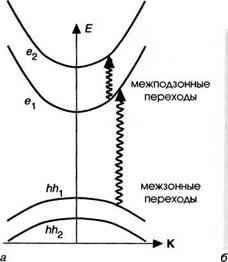
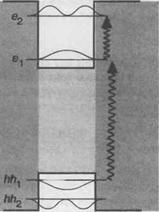
Сейчас нас будут интересовать переходы между различными состояниями в квантовой яме под влиянием синусоидально изменяющегося во времени возмущения, например, электромагнитной волны. Можно представить себе три типа переходов: (I) — межзонный переход, при котором электрон в валентной подзоне может быть возбужден в подзону проводимости; (II) — межподзонный переход, при котором электрон перемещается из одной подзоны в другую, оставаясь в той же самой зоне; (III) — внутриподзонный переход, при котором электрон переходит в различные состояния К в пределах той же самой подзоны п.
Последний тип перехода может иметь место вследствие процесса рассеяния, как это уже обсуждалось в контексте поглощения на свободных носителях в дополнении 7. В. В этом случае для осуществления необходимого обмена импульсами между электроном и решеткой требуется взаимодействие с фононом или примесью (смотрите рис. 7.В.2). Два другие типа переходов для случая взаимодействия с электромагнитной волной представлены на рис. 8.11. Новым моментом, вводимым двумерным аспектом квантово-размерной системы, является то, что межподзонные оптические переходы являются разрешенными в первом порядке. Очевидно, что в объемном материале такой процесс запрещен. Этот важный механизм мы будем обсуждать в следующем разделе.
 В случае межзонных переходов мы можем рассчитать скорость перехода, используя золотое правило Ферми. Рассмотрим волну, проходящую через яму:
В случае межзонных переходов мы можем рассчитать скорость перехода, используя золотое правило Ферми. Рассмотрим волну, проходящую через яму:
|
|
|
Рис. 8.11. Оптические переходы в пространстве К являются вертикальными. Представлены 2 типа переходов: слева — в обратном пространстве (а), справа — в реальном пространстве (б). |
Е(г, t) = Е, cos(q • г - Ш) = -|е, exp[i(q • г - й*)]+-|е; ехр[- i(q г - cat)] (8.51)
Потенциал взаимодействия электрического диполя (смотрите раздел 3.2 и дополнение З. Г) электронов в квантовой яме есть:
|
(8.52) |
![]() К,(г> 0 = ~еЕ ■ г = -|Е, • rexp[i(q • г - «/)]+ К. с.
К,(г> 0 = ~еЕ ■ г = -|Е, • rexp[i(q • г - «/)]+ К. с.
Скорость перехода из состояния у/*пК в валентной зоне в состояние у^тК, в зоне проводимости в соответствии с золотым правилом дается соотношением:
S(nK -> тК') = ^_е2|(тК'|Е, . г|яК)|2<У(^к. - Е;к - ha) (8.53)
По сравнению с объемным случаем (смотрите уравнение (7.10)) в рассматриваемой ситуации имеет место изменение дипольного матричного элемента:
(mK'jE, • г|иК^ = - jjC‘*(z)u*0(r)e-iK'RE, • геі, г^„"(г)иу0(г)е'ІККсІг (8.54)
Идя по тому же пути, как это уже неоднократно делалось в этой главе, и учитывая, что огибающая функция изменяется медленно по сравнению с постоянной решетки, мы можем выделить быстро и медленно изменяющиеся части, положив г = г' + (К., г.), где г' принадлежит элементарной ячейке, а г. = (К., £.) обозначает положение /-той элементарной ячейки. В этом случае интеграл превращается в сумму по /:
![]()
|
I(K+q-K')r' |
![]()
|
(8.55) |
![]()
![]()
|
Г * J сігЧоГ'Е, • г'м„о(г')е |
![]() Г, * i(K+q-K'K
Г, * i(K+q-K'K
+ Eq • г jdr«fo(rXor
Cell
Где а1 есть постоянная решетки в направлении ъ Последнее приведенное уравнение не поддавалось бы трактовке, если бы не наше умение сделать определенные упрощающие предположения. Начнем с того, что заметим в сумме по К. проявление закона сохранения для параллельных компонент импульса К+ ц — К' = 0. Поскольку волновым вектором излучения можно пренебречь по сравнению с волновыми векторами электрона КиК'в зоне Бриллюэна, это требование к импульсу учитывается дельта-функцией Кронеккера Дк к„ что приводит к ненулевому вкладу только для К = К'. По этой же самой причине сумма по г. может быть заменена интегралом, что приводит к следующему выражению для первого интеграла:
|
|
(8.56)
В этом выражении мы обнаруживаем матричный элемент гус для г перехода между валентной зоной и зоной проводимости.
В дополнение к этому, если протяженность волновых функций (~ толщине квантовой ямы) очень мала по сравнению с длиной волны Л, то в этом случае мы просто имеем:
|
(8.57a) |
![]() A =,K-Eq-r, c(/n, c|n, v>
A =,K-Eq-r, c(/n, c|n, v>
При этом
|
|
(8.576)
Во второй части уравнения (8.55) экспоненциальное выражение под знаком интеграла является практически константой, т. к. Л»аг, а К и К' далеки от края зоны Бриллюэна (в противном случае аппроксимация огибающей функции не действительна), при этом ортогональность блоховских функций устраняет этот член.
Таким образом, скорость перехода составляет:
5(иК -> /иК') = Ц— |Е„ • г„с|2|(т, с | п, v^S(Es - Лю)Дк к. (8.58а)
При этом:
„ с П2К2 , ,| Й2 К2 _ „ П2К2 Ь2К2 /овол
£--е-*^-м*т^г+£-=£“*^г+^г <8-5ад
В связи с этим отметим, во-первых, что сохранение полной энергии вводит порог для оптического поглощения Нсо > Е^ТС5Ш(1 ^ + К1 > Таким образом, порог
Оптического поглощения в квантовой яме испытывает коротковолновый сдвиг по сравнению с поглощением объемного полупроводника на величину, равную сумме энергий ограничения в зоне проводимости и валентной зоне. Этот коротковолновый сдвиг используется для определения физических параметров квантовой ямы (состав барьеров, толщина ямы...). Скорость генерации электронно-дырочных пар равна числу переходов в секунду:
(8.59)
В этом выражении вероятности заселенности обеспечивают присутствие электрона в начальном состоянии |п, у) и незаполненное конечное состояние |/и, с). Сохранение энергии и параллельной компоненты импульса определяют К как функцию энергии фотонов:
|
П2К2 2 тг |
|
= Псо-Е-е' -е: |
|
П2К7 |
|
— + — Тг т„ |
|
|
Здесь: тг есть приведенная масса. При термодинамическом равновесии в качестве следствия получаем:
|
И- |
Е: |
-е;(Па))- Ег " |
|
V |
Квт ) |
|
1 |
|
1 +ехр |
|
/ЛЮ = //М= |
![]()
|
(8.61) |
![]()
|
(8.62) |
![]() Е" ^=]?{^~Е* ~ е'т ~ /;(Ю = /;М= —
Е" ^=]?{^~Е* ~ е'т ~ /;(Ю = /;М= —
|
Ес- |
К |
- ест (рсо)- Ег ' |
|
КвТ |
|
1 + ехр |
К (М= А - - Е1 - £» - < |)
|
Ь2К: 2 тг ' Ь2К2 2 тг |
![]() Для переходов между валентной подзоной п и подзоной проводимости т мы можем просуммировать по К:
Для переходов между валентной подзоной п и подзоной проводимости т мы можем просуммировать по К:
— TOC o "1-5" h z |Е, гте|!К«, V | т, с)|2х^-У //(К)[1 - /;(К)]<5 2й " 1 А
-|ЕЧ • г„с|2|(а?, V I т, с)|" х | (Ьсо)^ - /тс(Ь0))б
Ке
2 Ь
Или
=—е2|Е, • г„е|2|(я, V I т, с)|2 ^-хв(П0)- ЕЛМ) //(йю)[1 -(йю)] (8.63а)
|
Дипольныи момент |
![]()
|
Плотность состоянии |
![]()
|
Вероятность заселенности |
![]() 2Ь лЬ, „______ /
2Ь лЬ, „______ /
Это выражение мы можем вновь переписать в виде:
= — |Е, • т„21{«, v|m, c)|2^-x в(г, со - )// {%(о% - /я‘ М] (8.636)
2Н 7lfl
Скорость межзонных переходов для квантовой ямы (с-1 см-2)
В этом выражении можно увидеть произведение дипольного момента и элемента перекрытия (п, v |/и, с), комбинированную плотность состояний для двумерного случая, mjfi2, а также соответствующую статистику заселенности. Таким образом, скорость генерации Gmn является произведением коэффициентов статистики /ш и /п, которые зависят от температуры, положения уровня Ферми и скорости генерации G° = что имело бы место в случае, когда fm( ~ fn) было бы равно единице и
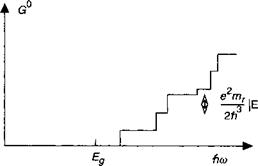
Зависело лишь от структуры. Это иллюстрируется рисунком 8.12.
|
Рис. 8.12. Скорость генерации в собственной квантовой яме ступенчатого профиля. Всякий раз, когда становится возможным новый подзонный переход при заданной энергии поглощения, скорость генерации возрастает на ступеньку. Порог генерации пары располагается по шкале энергий выше эквивалентной запрещенной зоны объемного материала. |
Перекрытие огибающих функций |(т, с п, у)|2 позволяет ввести правила отбора. Например, в симметричной квантовой яме переходы между подзонами с различной четностью запрещены. В случае подзон, лежащих глубоко в яме, огибающие функции для электронов и дырок практически идентичны так, что возможны только переходы между состояниями, обладающими одинаковыми индексами (т = п).
Анализ, проведенный для переходов, индуцированных поглощением, между валентной зоной и зоной проводимости дает совершенно те же результаты для стимулированного излучения (в этом случае участвуют переходы между зоной проводимости и валентной зоной) за исключением статистики заселенности. Стимулированная рекомбинация за счет поля имеет вид:
К = X ■Б -{По}) (8-64)
При этом баланс генерации—рекомбинации из-за поля имеет вид:
— ] = — |Е„ ■ г«Г X (т, сп, у)^в(Пю - Е, ьм '{[„"(По))- /тс(М] (8-65)
К (1/ упеЛ 2/? Я/? и, т
Баланс скорости оптической генерации - рекомбинации для квантовой ямы (с-1 см-2)
И, наконец, вспомним, что для двух блоховских функций с собственными состояниями, имеющими одинаковые к в различных зонах, справедливо соотношение:
Ы1Н > Г] |«Л> = (ЕЛ - £*)(«* I Г |Ма) = («ск| Р |МИс) (8.66)
Т„
Как было показано ранее в главе 7, матричный элемент гус может быть выражен через матричный элемент Кейна, использованный в дополнении 5.В в рамках к • р - метода:
1» <м7> Г = р
" Еет0 Р"
Мы можем задуматься над тем, следует ли заменять член Eg в (8.67) на со в выражениях для скорости генерации, чтобы учесть фотоны с энергией, превышающей ширину запрещенной зоны. Однако, мы не должны слишком много требовать от аппроксимации огибающей функции, которая применима лишь до тех пор, пока Н со— Е^/Е «1.
Тот факт, что вырождение валентной зоны приводит к возникновению отличных друг от друга подзон тяжелых и легких дырок имеет в качестве следствия то, что матричный элемент гус зависит от типа перехода. С использованием волновых функций дырок дополнения 5.В читатель может убедиться в справедливости правил отбора, приведенных в таблице 8.1.
|
Табл. 8.1. Изменение ориентации электрического поля по отношению к квантовой яме приводит к правилам отбора для переходов гж в уравнении (8.65) равным величине гж в объемном материале, умноженной на коэффициент, приведенный в таблице
|
В частности, переходы между электронной подзоной и подзоной тяжелых дырок запрещены для ТМ-поляризации (т. е. для электрического поля, перпендикулярного границам квантовой ямы — смотрите главу 9).