Оптические межподзонные переходы в квантовой яме
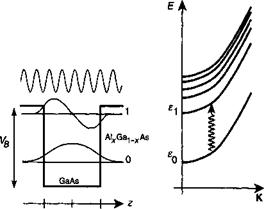
При межподзонном переходе начальное и конечное состояния электрона принадлежат одной и той же зоне. Это приводит к правилам отбора и характеру, полностью отличным от тех, что наблюдаются при межзонных переходах. Для конкретизации давайте предположим, что этой зоной является зона проводимости (смотрите рис. 8.11). В этом случае начальными и конечными состояниями являются:
!/„к = -7=С,(г)ехрОК КК0(г)
*(8.68) ¥„к = -^Са(1)ехр(1К'-К)ис0(.т)
При этом в них входят те же самые блоховские функции «с0(г).
Золотое правило Ферми вновь дает нам скорость перехода, индуцированного электромагнитным полем (уравнение (8.53)). Для матричного элемента единственное различие между уравнениями (8.54) и (8.55) заключается в том, что начальное состояние также находится в зоне проводимости.
(»К'|Е, • г|„К) = £
|
КК+ч-К')*, |
1У х1У у / /
Г - і ' * / '¥-> ' / /Ч КК+я-К')У ( , * «К-ц-К'К
|
О- |
J <ІҐ ис0(т )Е, • г «с0(г )е + Е, • г, ] йт ис0(т) ис0(т )е
Здесь сумма по К., очевидно, связана с сохранением импульса в параллельном направлении. В том, что касается первого интеграла, матричный элемент г' в данном случае равен нулю, так как и^г) преобразуется как 1 при операциях кубической симметрии кристаллической решетки.
Второй интеграл в (8.69) в этом случае дает £2сс11, когда изменение экспоненциального члена пренебрежимо мало в пределах элементарной ячейки. В результате, нам остается сумма:
/2 = I е^Ч •, (8.70)
/. * У
При этом ее, в свою очередь, можно обратить в интеграл в направлении £
|
1,= |
|
N |
|
1 уекк+ч-к, к,гс(г^.г^№ К™ у іх, і ^ |
 |
|
|
|
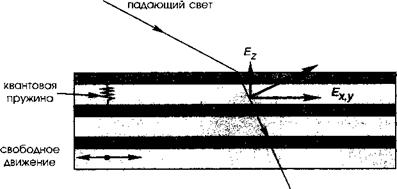
Поскольку огибающие функции ортогональны, этот последний интеграл приводит к межподзонному правилу отбора, гласящему, что переход может вызвать только Е - компонента (смотрите рис. 8.13).
Интеграл (8.71) может быть записан в виде:
|
(8.72) |
Это приводит к скорости перехода:
|
(8.73а) |
Я(пК -> юК') = ^-ЕЛ{т^пр(£т-£„-к^^
|
-6/2 6/2 Рис. 8.13. Квантовая яма с двумя связанными состояниями (а) и соответствующие дисперсионные кривые полной энергии Е {б), приводящие к наличию столь большого количества подзон. Поскольку подзоны параллельны, переходы при постоянном К приводят к энергетическим резонансам (т. е. переходы с одной и той же энергией имеют место в широком диапазоне значений К между парами подзон). |
|
Рис. 8.14. Зависимость скорости возбуждения фундаментальной подзоны от энергии фотонов. Подзоны в квантовой яме приводят к дискретным переходам (переходы из связанного состояния в связанное состояние). Над барьерами подзоны формируют континуум и могут участвовать в переходах между континуумом и связанными состояниями. |
|
А |
Заметим, что в этом последнем выражении аргумент в ^-функции Дирака более не зависит от К, поскольку подзоны параллельны (рис. 8.14). Таким образом, даже если оптические переходы приводят к взаимодействию между светом и делокализо - ванными электронными состояниями в среде (о чем свидетельствует существование энергетической подзоны), это взаимодействие тем не менее является резонансным, как если бы система обладала дискретными уровнями!
Энергия фотонов, резонансная с уровнями в квантовой яме определяется соотношением:
Но) = £т-еп (8.736)
Для установления скорости электронных переходов из одной подзоны в другую должны быть применены статистические соображения, как это уже имело место в случае меж - зонных переходов. В результате этого скорость возбуждения—релаксации может быть получена суммированием по К:
С ^ 4Е - /.(К)] <8-74>
Поскольку Я(пК —> тК) не зависит от К результат получается особенно простым:
В =
(8.75)
Скорость оптической генерации—рекомбинации (с-1 см-2)
Здесь: пп и пт — соответственно концентрации электронов в подзонах пит. Зависимость <7 от энергии фотонов представлена на рис. 8.15, и она существенно отличается от зависимости, приведенной на рис. 8.12 для межзонных переходов. В (8.75) мы узнаем также выражения (1.86) и (3.63), установленные в процессе обсуждения атомных переходов между дискретными уровнями. Такие переходы между связанными состояниями в квантовой яме называются переходами из связанного в связанное состояние.
Над барьером подзоны не образуют дискретный спектр. В этом случае огибающие функции являются протяженными, а энергетические уровни свободными. Их можно классифицировать по компоненте к их волнового вектора в барьере:
|
Рис. 8.15. При межподзонных переходах лишь компонента электрического поля, перпендикулярная квантовым ямам, может оптически взаимодействовать с «квантовыми осцилляторами», возникающими из-за допустимого смещения. В то же время для параллельной компоненты поля остается возможность слабого взаимодействия со свободным двумерным электронным газом. |
|
(8.76) |
К' 2 - т=£* (г)ехр( ІК' • 11)ис0(г)
Теория скорости возбуждения следует из простого обобщения (8.75) при замене суммирования по т на интегрирование по к (смотрите Дополнение 1.А):
|
Л2 к* 2 тК |
|
|
|
|
|
|
|
|
Мы предположили, что заселенность состояний в барьере п^ пренебрежимо мала. Заметим, что при всех энергиях фотонов Н СО > Ув — €п явно возможными являются переходы из подзоны п в континуум. Эта ситуация аналогична явлению фотоионизации, которого мы касались в дополнении 1.А и к которой вновь более детально возвратимся в главе 11 при изучении квантово-размерных детекторов.
