Оптоэлектроника

Гармонический осциллятор

Исследование гармонического осциллятора в квантовой механике обеспечивает широкое поле для чисто физических ассоциаций. Поэтому мы дадим квантово­механическое описание электрона, упруго связанного с притягивающим центром. Эта система одинакова пригодна для описания поведения электрона в поле ядра, колебаний атомов в кристалле или даже, как мы увидим далее в главе 2, для описа­ния специфических электромагнитных волн, которые иначе называются фотонами.

Теперь мы рассмотрим частицу массой т в условиях воздействия притягиваю­щего одномерного параболического потенциала:

К(х)=1^ (1.Г.1)

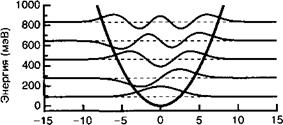
Где к — коэффициент упругости квантово-механической пружины (смотрите рису­нок 1.Г.1).

Следует отметить, что обобщение этой задачи на трехмерный случай не пред­ставляет особых теоретических трудностей. Однако одновременно с этим обилие необходимых индексов усложняет описание, не очень расширяя его содержание. В рассматриваемом случае гамильтониан частицы может быть записан в виде:

Н гта>1х> (1.Г.2)

2т 2

Классический гамильтониан гармонического осциллятора

Где со0 — резонансная частота системы:

(1.Г. З)

Классическое поведение системы в рассматриваемом случае хорошо известно: сис­тема колеблется, при этом положение частицы дается соотношением:

:с! ак (0 = ХовІпЦ*+ 0)

Где х0 — амплитуда колебаний, а ф — их фаза. Для квантово-механического описания частицы и нахождения стационарных состояний необходимо решить уравнение:

(1.Г.5)

Принцип соответствия дает нам форму уравнения Шредингера в координатном t (Р = — (с1/с1х)) представлении:

Ч~~Т~¥(х)+ та>$хгі/(х)= Еу/(х) 2т ах 2

Уравнение Шредингера для стационарного одномерного гармонического осциллятора

Наша задача заключается в нахождении физически допустимых решений этого уравнения (т. е. квадратично интегрируемых решений). Это дифференциальное урав­нение может быть решено многими различными способами (например с использо­ванием полиномов). Однако намного более эффективно решить эту задачу с ис­пользованием алгебры операторов, впервые разработанной П. А.М. Дираком. Нач­нем с того, что введем безразмерные операторы:

(1.Г.7)

У]тПсо0 Р

В этом случае гамильтониан может быть записан в виде:

Н = Нсо0Н

Где безразмерный оператор Й дается соотношением:

* 1

Й=-[Х2+Р2]

Вспомним соотношения антикоммутации между операторами координаты и импульса, которые записываются в виде:

[х, р = хр - рх = П где для безразмерных операторов справедливо соотношение:

[*,?]= І

Теперь мы покажем, что это соотношение антикоммутации (которое просто представляет собой переформулировку первого принципа неопределенности Гей­зенберга) также приводит к квантованию энергии. Таким образом, мы ищем реше­ние системы:

[*>?]= І

I

Определение операторов рождения и уничтожения

Операторы координаты и импульса даются соотношениями:

Х = -- (а + а+) У 2/и<м0

(1.Г.14)

По причинам, которые вскоре станут понятными, а мы будем называть операто­ром уничтожения, а а+ оператором рождения. Рассчитаем теперь произведение а+ а:

Или

А'а = ^(Х:! + рі +

Таким образом:

Так что:

(1.Г.16)

Уравнение (1.Г.16) является, таким образом, выражением принципа неопреде­ленности на языке операторов рождения и уничтожения. Введем далее оператор № Ы = а+а (1.Г.17) Оператор N называется оператором числа. Гамильтониан гармонического ос­циллятора и оператор числа связаны соотношением:

(1.Г.18)

Теперь мы покажем, что собственные значения N являются либо целыми поло­жительными числами или равны нулю. Для этого нам необходимо доказать три теоремы. Пусть IV) будет собственным вектором N с собственным значением уили:

Щу) = уу)

(1.Г.19)

Теорема 1: Собственные значения оператора N либо положительны, либо равны нулю.

Переписывая (1.Г.19) в виде:

Ц + ц|v) = v|v)

Мы можем спроецировать это уравнение на |v) с тем, чтобы получить:

(v|tf + tf|v) = v(v|v) = V Это может быть также записано в виде:

(va*av)= (a|v))(a|v))= |(ц|v))|2

Так что:

HMI2

Из этого мы выводим, что у является неотрицательным и что:

V = 0, если только av) = 0. (1.Г.20)

Теорема 2: Если | v) является собственным вектором N с собственным зна­чением v, то av) тоже является собственным вектором N с собственным

Значением v - 1.

В самом деле,

Nav) = ^а + а j a|v)

Поскольку соотношение антикоммутации требует, чтобы аа+ — а+ а = 1, это последнее соотношение может быть записано в виде:

Nav) = i^aa -^av) = a^a - 1 = a{N - l)|v) = (у -

Что мы и хотели доказать.

Теорема 3: Если | v) является собственным вектором N с собственным зна­чением v, то a+v) также является собственным вектором N с собственным

Значением v + 1.

Аналогично тому, как этот было сделано выше, запишем:

Na+v) = = а+^аа j|v)

= а + ^1 + аа j|v) = я (l + W)|v)

= (v + l)a + |v)

Теперь мы уже в состоянии найти собственные значения N. Предположим, что v, собственное значение N, является нецелым и неравным нулю с п — Int(v), где Int означает целую часть числа. Тогда av) есть собственный вектор N с собственным

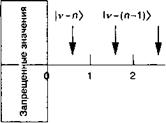
Значением V— 1; a2v) есть собственный вектор с собственным значением v— 2, anv) есть собственный вектор с собственным значением у — п = у — Int (v), которое должно лежать между 0 и 1 (смотрите рисунок 1.Г.2). Так как v является нецелым,

V — п должно быть отлично от 0, при этом an+lv) должно иметь собственное значе­ние v — п — 1, которое должно быть отрицательным. Это однако невозможно по теореме 1. Величина v должна быть такой, при которой вектор an+lv) не может существовать, т. е. ап|v) = 0. Таким образом, собственные значения у оператора N являются либо положительными целыми числами или равны нулю. Поскольку мы можем получить из собственного вектора |т) любой другой собственный вектор |п), применяя т — п раз увеличивающий или уменьшающий операторы а+ или а, соб­ственными значениями оператора N является весь ансамбль положительных целых чисел, т. е.:

Nn} = пп}, п = 0,1, 2,...

|v-1> |v>

J_______ L

Л-1 п

Рис. 1.Г.2. Каждое действие оператора уничтожения приводит к уничтожению оди­ночного кванта возбуждения.

Из соотношения (1.Г.18) мы видим, что энергии стационарных состояний гар­монического осциллятора квантуются и даются соотношением:

Hco0, п = 0, 1, 2,...

Энергетические уровни одномер­ного гармонического осциллятора

При этом стационарными состояниями являются собственные состояния |п) опера­тора числа. В таком случае энергетический спектр гармонического осциллятора со­стоит из серии эквидистантных уровней, разделенных по энергии интервалами Ь со0 (смотрите рисунок 1.Г.1).

Теперь попробуем выяснить, как действуют операторы а и а+. Из теоремы 2 нам известно, что ап) является собственным вектором N с собственными значениями п — 1. Так как мы видим, что энергетические уровни одномерного осциллятора являются невырожденными (что может быть легко доказано), это означает, что ап) пропорционально |п — 1). Таким образом:

Ап) = сп — 1), п = 1, 2,...

Но модуль ап) дается соотношением:

|(а| и)]2 = (<я| п)) (а| п))= (п |а+а| п) = (п |7У| п) = п

Так, что с2 = п, с помощью чего мы получаем:

Ап) = 4пп -1), п = 1, 2,... (1.Г.23)

Совершенно аналогичным образом мы получаем для а+:

А + п) = у/п + \п + 1), л = 0, 1,... (1.Г.24)

Теперь мы уже в состоянии лучше понять трактовку проблемы в рамках опера­торной алгебры Дирака. Начать с того, что каждое индивидуальное квантовое состо­

Яние обладает большей энергией по мере увеличения п. Уравнение (1.Г.23) показы­вает, что действие оператора а проявляется в инициации перехода между состоянием с квантовым числом п и состоянием с квантовым числом п — 1. Таким образом, оператор а удаляет из системы квант возбуждения, соответствующий Н со0. Важно помнить, что операторы а и а+ не являются эрмитовыми и не обладают собственны­ми значениями в виде действительных чисел. Уравнение (1.Г.24) может быть исполь­зовано как рекуррентное соотношение для генерации всех состояний |п) оператора Я:

|«) = ^1|0) (1.Г.25)

У/П

Теперь обратим наше внимание на состояние |0). Оно является основным со­стоянием системы и обладает минимальной возможной энергией:

Е0=±Ла>0 (1.Г.26)

В противоположность классическому осциллятору, у которого минимальное энергетическое состояние является нулевым (или состоянием покоя), минималь­ное энергетическое состояние квантового гармонического осциллятора — ненуле­вое. Это удивительное наблюдение следует из соотношения антикоммутации (1.Г.16), которое представляет собой переформулировку первого соотношения неопределен­ности Гейзенберга. Таким образом, мы могли бы попробовать вывести этот резуль­тат непосредственно из применения принципа неопределенности, утверждающего, что неопределенности по х и по р связаны соотношением:

АхАр ~ Ь. (1.Г.27)

В рамках классического подхода полная энергия основного состояния частицы дается соотношением:

Е =^ + тсо^х2 (1.Г.28)

Подставляя (1.Г.27) в (1.Г.28), получаем выражение для энергии в виде:

<,т'29>

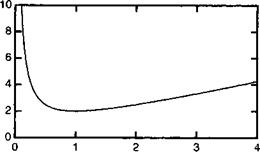
Характер изменения Е в зависимости от Ах иллюстрируется рисунком 1.Г. З. Как видно из представленного рисунка, кривая достигает минимума при:

Л * П

Ах ■

Р1

тй)0

Что соответствует минимальной энергии Е= йсо0. Это совсем неплохо для эвристи­ческого подхода !

Теперь нашей задачей является нахождение собственных состояний в коорди­натном представлении, т. е. нахождение волновых функций стационарных состо­яний. Начнем с основного состояния и применим оператор уничтожения (1.Г.20):

Рис. 1.Г. З. Зависимость приведенной энергии гармонического осциллято­ра от неопределенности параметра приведенного положения в соответ­ствии с (1.Г.29).

Я|0) = 0 (* + і?)0) = 0

Возвращаясь к определению (1.Г.7), находим, что в координатном представлении:

Х + Ь

Л1тЬсо0 &х

Или вновь:

Т со

Хфа(х)+ — ф0(х)= О п ах

Легко установить, что решением этого классического дифференциального урав­нения является функция Гаусса вида:

(1.Г.31)

/2)

Волновые функции с большими значениями индекса могут быть получены ре­куррентным образом. Теперь мы уже в состоянии сделать некоторые предсказания по поводу измерения квантовых наблюдаемых. Например, средняя величина поло­жения частицы в состоянии |п) дается соотношением:

X = (х) = (и|х| п) = + а+ )")

С учетом того, что а+п) = уіпп — 1), и поскольку п) и п — 1) являются ортого­нальными собственными векторами ЛГ, обладающими различными собственными значениями, средняя величина х является таким образом нулевой (что не удиви­тельно с учетом симметрии системы). Для расчета средне-квадратичного значения положения перепишем оператор х2 с использованием операторов а и а+:

, Ь ( , + + Ь/ 7 і -> + (1.Г.32)

Х2 =--------- (а2 + а+2 + аа + а а)=------------ (а2 + а+2 + 1 + 2а а)

2тсо0 2тсо0

Среднее значение квадрата наблюдаемое для данного состояния |п) в таком слу­чае есть:

Х2 = (пх2п) =-------- (па2 + а+2 + 1 + 2а+а п)

Х 1 1 1 2тсос ' 1 1 1

Поскольку операторы а2 и (а+)2 направляют |п) в состояния, которые ортого­нальны (п, вклад этих операторов нулевой, из чего следует:

(1.Г. ЗЗ)

Таким образом, чем больше энергия моды квантового осциллятора, тем больше и степень неопределенности в положении частицы.

Нас могло бы шокировать, обнаружив, что ожидаемая величина положения части­цы в индивидуальных собственных состояниях осциллятора не осциллирует в реальном пространстве. Мы увидим, что создание состояний с изменяющимися во времени ожидаемыми величинами, согласующееся с нашей классической физической интуи­цией, потребует конструировать тщательно выбранные линейные комбинации (состо­яния Глаубера) на основе этих более фундаментальных стационарных состояний.

Классический пример------------------------------------------------------------------------------------------

Рассмотрим сферу массой в 1 г, подвешенную на пружинке т и имеющую соб­ственную частоту колебаний 1 кГц. Квантовая неопределенность положения в ос­новном состоянии дается соотношением (1.Г. ЗЗ) при п — 0 и составляет Дх =10"17 м! Очевидно, что квантовый характер такой системы пренбрежим.

Квантовый пример: фононы Эйнштейна----------------------------------------------------------------

Рассмотрим теперь периодическую цепочку взаимодействующих атомов, образую­щих кристаллическую среду. Потенциальные ямы, связывающие каждый из атомов с соседними обладают минимумом энергии при относительном расстоянии между атомами г0. Поблизости от положения равновесия гамильтониан любой пары со­седних атомов может быть аппроксимирован соотношением:

(1.Г.34)

Где хг и рг соответствуют расстоянию и моменту каждого атома, а и" есть вторая производная потенциала в минимуме распределения. Тогда каждая пара атомов образует гармонический осциллятор с резонансной частотой:

(1.Г.35)

Мы можем аппроксимировать кристаллический потенциал периодическим по­лем, обладающим типичной амплитудой модуляции 5 эВ с периодом 0,5 нм. В этом случае потенциал может быть записан в виде:

И вторая производная и" равна 5 эВ х 4/г2/(0,5 нм)2 или 126 кг с-2. Для атомов, содер­жащих приблизительно 50 нуклеонов (т. е. имеющих маСсу 8,35 х 10 26 кг) собственнАя частота колебаний атомов дается (1.Г.35) составляет ^(126 кг с_2/8,35 х 10-26 кг)/2/г или 6 х 1012 с-1. Эти решеточные колебания (называемые продольными фононами или фононами Эйнштейна) по своему спектральному диапазону соответствуют инфракрас­ному диапазону спектра, обладая энергией взаимодействия порядка 25 мэВ.