New developments in advanced welding

Gas tungsten arc welding

B. L. JARVIS, CSIRO Manufacturing & Infrastructure Technology, Australia and M. TANAKA, Osaka University, Japan

3.1 Introduction

Gas tungsten arc welding (GTAW) first made its appearance in the USA in the late 1930s, where it was used for welding aluminium airframes. It was an extension of the carbon arc process, with tungsten replacing the carbon electrode. The new tungsten electrode, together with an inert helium shielding gas atmosphere, reduced weld metal contamination to the extent that highly reactive metals such as aluminium and magnesium could be welded successfully. For a time the process was known as ‘heliarc’ in the USA. Other countries substituted the less expensive argon for helium and referred to the process as ‘argon-arc’. Later these distinctions were dropped and the process became known as tungsten inert gas (or TIG) welding. More recently the term gas tungsten arc (GTA) has been introduced to signify that the shielding gas may not necessarily be inert.

GTAW is known for its versatility and high joint quality. It can be used with a wide variety of materials, including highly reactive or refractory metals. It may be operated manually at lower currents (e. g. 50 to 200 A) for single pass joining of relatively thin sections, or multi-pass welding of thicker sections that have appropriate V - X - or similar type edge preparations.

During the 1960s the process was extended to much higher currents, allowing the arc forces to play a significant role in increasing weld penetration. At currents above about 250 A the arc tends to displace the weld pool, with the effect increasing as the current is increased further. This mode of operation is generally automated, and in its early manifestations gave rise to terms such as high current, buried arc, and sub-surface arc TIG (or GTAW). Plasma arc welding also has its origins in the GTAW process. More recent innovations have included the introduction of active fluxes (A-TIG), dual shield GTAW, guided GTAW, keyhole GTAW and laser-GTAW hybrid processes.

Understanding of the GTAW process involves input from many disciplines. Although appearing relatively simple, application of the process involves

many choices including electrode size and composition, electrode tip geometry, power supply characteristics, electrode polarity, shielding gas, welding current, and voltage settings. Each of these will be related to the type of material and its joint geometry. The complexities and the importance of the GTAW process have stimulated research which is still very active more than 60 years after its introduction.

3.2 Principles

3.2.1 Energy transport

GTAW utilises an intense electric arc formed between a non-consumable tungsten electrode and the workpiece to generate controlled melting within the weld joint. Essentially the arc can be used as if it was an extraordinarily hot flame. The stability of the tungsten electrode and the option to use totally inert gas mixtures if desired means that the process can be very clean and easy to implement. It is also a process with the potential to deliver relatively high power densities to the workpiece, and so can be used on even the most refractory metals and alloys. It can be misleading to refer to arc temperatures as a measure of melting ability, but the intent can be captured in the measure of power density. Using this one finds that GTAW processes produce power densities at the weld pool of up to 100 W/mm2. For comparison this is at least an order of magnitude greater than is available from an oxy-acetylene flame. The power density delivered to the workpiece is important in determining the process efficiency and can be a significant constraint when dealing with highly conductive metals such as copper.

Under standard conditions all shielding gases are extremely good electrical insulators. The current densities typical of welding arcs (of the order of tens of amps per square millimetre) can only be achieved if a high concentration of charged particles can be generated and maintained in the conducting channel. In arcs the necessary populations of electrons and ions are maintained by thermal ionisation and this requires temperatures of about 10000K and above.

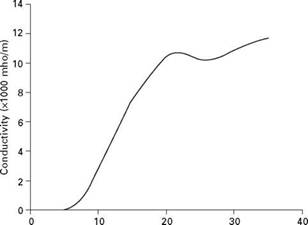
The degree of ionisation of a gas can be expressed as a function of temperature by the Saha equation (Lancaster, 1986). The resultant conductivity is then determined from consideration of the charge mobilities, as can be found in standard texts, e. g. Lorrain and Corson (1970) and Papoular (1965). An example of how the conductivity of argon varies with temperature is shown in Table 3.1 and presented graphically in Fig. 3.1. The data is taken from Lancaster (1986).

It is now known that the current density in an arc column has a limiting value under normal conditions. Once this limit is reached further increases in total current only distribute the current over larger areas of the anode, with

3.1 Plot of the electrical conductivity of argon from 3000K to 30000K.

no appreciable change in peak current density on the arc axis (Jackson, 1960). In the case of argon the conductivity increases until doubly ionised argon appears at about 22000 K. At this point the resistance provided by the doubly charged ions outweighs the benefit of the increased number of electrons
and so conductivity reaches a local maximum (see Fig. 3.1). Once this temperature has been reached in a particular region further increases in current will tend to generate a spreading of the current distribution into the adjacent, slightly cooler regions (Shaw, 1975).

For a very preliminary exploration of the welding arc, its main section can be treated as one-dimensional, i. e. as a function of radius, r, only. Such an approach, introduced by Glickstein in 1981, began with a simple model for the positive column in which ohmic heating was balanced against radial thermal conduction:

[3.1]

In this equation s is the electrical conductivity, E the electric field, r the radius from the arc axis, к the thermal conductivity and T the temperature. Equation [3.1] is known as the Elenbaas-Heller equation. This equation can be corrected for additional energy losses through radiation, S(T), (Lancaster, 1986) and it is then known as the ‘corrected Elenbaas-Heller’, equation

[3.2]:

[3.2]

Since the electrical and thermal conductivities of shielding gases have complicated temperature dependencies, as shown in Fig. 3.1, these equations can only be solved numerically. Nevertheless, the view of an arc in which radial conduction and radiation balance ohmic heating is easily visualised and so is useful in developing a qualitative understanding of arc behaviour. For example, Glickstein’s solutions predicted that helium arcs should be much broader than those of argon despite peak temperatures and current density distributions being similar. Consequently, helium arcs should require higher voltages than argon arcs do - as is observed - since the energy is derived from the electric field. Similarly, it can be appreciated that vapour contamination or minor additions of a gas of lower ionisation potential should significantly alter the arc configuration.

An appreciation of the welding arc via the Elenbaas-Heller equation has two fundamental limitations: there is no consideration of the regions connecting the plasma to the electrodes and the omission of convection within the arc.

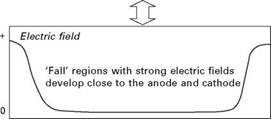
The very narrow regions between the electrode surfaces and the arc proper are known as sheath regions. In these regions the high temperatures (~10000K) needed for good electrical conductivity in the gas cannot be sustained due to the cooling provided by the cold electrodes (even the boiling temperature of iron is thousands of degrees below that required for argon to conduct well). Consequently, the electrical conductivity of the gas will be
extremely low (see Table 3.1). Because of the high resistivity close to the electrodes the electric field of the arc will be very much stronger in these regions than elsewhere. This is equivalent to saying that the field has a non­zero divergence and according to Maxwell’s equations must be associated with the presence of net electric charge:

V • E = ЄГ [3.3]

e0

Or, in one dimension:

P = e0§ [3-4]

Consequently, sheath regions will be bounded by regions of charge, one on the electrode surface and the other at the interface with the plasma. This latter constitutes a region of space charge. The corresponding voltage drops are sometimes known as ‘fall’ voltages (see Fig. 3.2).

The sheath regions are extremely important in determining the particular characteristics of an arc and in establishing the overall energy balance. In welding arcs the predominant charge carriers are electrons and these must be continually replenished by being drawn out of the cathode and across the cathode sheath. Liberating electrons from a metal surface requires a considerable amount of energy - each electron absorbing at least an amount ef where f is the work-function of the surface (typically 2-4 V). If the metal is suitably refractory (such as tungsten or hafnium) this can be provided by the high temperature of the electrode and is then known as thermionic emission. In this case the electrons effectively evaporate from the surface. If the temperature of the electrode is not high enough the electrons must gain their energy from the very high strength field between the surface and the surrounding space charge. This is termed field emission. GTAW is generally operated in the thermionic emission mode. Electron emission is aided by the presence of oxides and other surface impurities.

The electrons leave the arc by crossing the anode sheath and entering the anode, which is usually the workpiece. The anode sheath is believed to be of the order of one electron mean free path in width, to be consistent with its relatively low temperature. In crossing this and entering the anode the electron transports a considerable portion of the total energy flux. The energy contribution of each electron to the anode includes its thermal energy, the energy it absorbs from the anode fall, and its energy of condensation, ef. In some cases this can amount to as much as 80 % of the total energy flow into the anode. The other major source of energy transport to the anode is conduction and here the characteristics of the shielding gas become important. For example, helium is far more conductive than is argon and consequently delivers more heat - hence the perception that it makes an arc ‘hotter’. Gases such as

Cooler sheath or fall regions of the arc

hydrogen and nitrogen exhibit what is known as ‘reactive thermal conductivity’. They dissociate at high temperatures with the absorption of significant amounts of energy, only to recombine and release this energy in the cooler regions such as the anode sheath. So these gases are also associated with ‘hot’ arcs. In addition to electron absorption and conduction, convection and radiation also transport energy. Convection in particular becomes very important as currents rise above 40 A or so (Zhu et al., 1992) and may be the dominating transport mechanism outside the sheath regions. Convective flow is powered
by Lorentz forces associated with the passage of the high welding currents, and has an impact on the momentum as well as on energy transferred to the weld pool. Present numerical models of welding arcs endeavour to incorporate all these effects (Lowke et al., 1992, Zhu et al., 1992) but there is still much development to be done.

3.2.2 Momentum transport

At currents below about 200 A the gas tungsten arc has many characteristics of an ideal flame. It can be chemically inert, it produces very high heat fluxes to the workpiece, and it appears to produce almost no disturbance to the molten metal it produces. But despite the absence of metal transfer the arc does transport momentum and this becomes important at higher currents. The momentum transfer and several of the resultant forces on the weld pool are due to Lorentz forces generated within the arc. These forces can give rise to high velocity plasma jets. Similar forces also occur within the pool and are one of the drivers for circulation within it. The strength of these forces is dependent on the magnitude of the welding current (F I2) and its geometric distribution. The latter dependency is in turn related to variables such as electrode composition and geometry, and choice of gas shield composition.

In order to model a welding arc one might begin by considering the motion of an individual element of the plasma. Thus each element of the arc fluid is accelerated in proportion to the net force acting on it:

p ddV = p^+ v • Vv j = (net force per unit volume) [3.5]

where ris the (incompressible) fluid density, v its velocity and t is time. The net force per unit volume in an arc will include the Lorentz term J X B, the pressure gradient - VP, and a ‘diffusion’ term that accounts for viscous damping, hV2v. The resultant equation is a modified Navier-Stokes equation for an incompressible fluid, and reads:

p dt = - pv • Vv - VP + J X B + hV2v [3.6]

Solving this equation for an arc is challenging since the parameters are strongly coupled, rendering the system non-linear. In general, several different equations must be satisfied simultaneously (e. g. conservation of mass, energy, charge and momentum) and numerical methods must be used for their solution. The work of Zhu, Lowke and Morrow (1992) provides a comprehensive treatment of this problem.

However, as is often the case, much can be learned by considering simplified approximations. One such approximation is to ignore viscosity, as did Converti
(1981). He treated the arc as a truncated cone with the welding current, I, flowing between the two electrodes, a tungsten tip with an emission area of cross-sectional radius Re and the weld pool surface of larger radius Ra. With the assumption that the current density is constant over any chosen radial cross-section, the net force normal to the pool was found to be:

[3.7]

The ratio Ra/Re is known as the arc expansion ratio.

Converti identified the two J X B components contributing to the net Lorentz force acting on the arc. Current flowing through an arc generates a circumferential magnetic field, Bg(r), perpendicular to both the axial and radial vectors. Consequently both axial and radial components of the arc current will interact with this field to give rise to forces. The axial component (Jz x Bg) generates a compressive, or pinch force while any radial component (Jr x Bg, due to arc expansion) results in an axially directed force. These two forces give rise to a radial pressure gradient and a fluid flow (the plasma jet), respectively. The radial pressure gradient produces a static pressure that squeezes the plasma against the terminating electrodes. On the other hand, the fluid flow contributes a dynamic pressure that acts only on surfaces that change the velocity of the fluid stream.

Evaluation of equation [3.7] indicates that the arc force increases with the square of the welding current. Furthermore, experimental observation (Erokhin, 1979) and calculations based on reasonable estimates of the arc expansion ratio (Jarvis, 2001) show that the magnitude is of the order of 3 x 10-5 I2 grams weight. So for example, an arc carrying 100 A would exert a relatively insignificant force of about 300 mg weight, whereas at 500 A the force would be nearer 7.5g weight. The latter is sufficient to displace a significant volume of weld metal, molten stainless steel having a density of about 7g/cm3.

Evidently the larger portion of the arc force derives from the dynamic pressure term (m/4p) ln (R a/Re). Consequently changing the arc expansion ratio will alter the arc force generated at a given current. Now, in the case where the tungsten electrode is the cathode there is good evidence that the emission current is approximately proportional to emission area. In fact, measured values for emission current densities vary slightly around about 150A/mm2, depending on electrode composition (Matsuda et al., 1990) and welding current (Adonyi-Bucurdiu, 1989). Consequently the arc expansion ratio can be increased by measures such as reducing the angle of the electrode taper or changing the electrode composition. Other factors, such as choice of shielding gas and electrode diameter can also alter the expansion ratio by changing the thermal balance at either electrode (see also Section 3.4.6).

The arc pressure is a measure of the arc force per unit area at any given point over the weld pool. Generally arc pressure is a maximum on or close to the arc axis and is often modelled as having a Gaussian distribution. Arc pressure is sensitive to changes in the distribution of the arc force and so is significantly altered by factors such as redistribution of the current and changes in gas viscosity. For example, the arc pressures in a helium arc are significantly lower that those in an argon arc at the same current because high-temperature helium is more viscous than argon and therefore distributes the arc force over a wider area.