New developments in advanced welding

Conventional view of keyholes in welding

Keyhole welding is usually identified with laser and electron beam processes. These two processes are known for their deep narrow keyholes, often with aspect ratios exceeding 10:1. Such keyhole cavities are approximately cylindrical and so have a strong tendency to collapse under the pressure due to surface tension (g/r for a cylindrical geometry) and the head of liquid metal (pgh). (In these expressions gis surface tension, r the radius of the keyhole channel, p the liquid metal density, g the acceleration due to gravity and h the depth). The accepted view is that these keyholes are maintained by an increased pressure in the cavity generated by the recoil from ablating material (Andrews and Atthey, 1976; Lancaster, 1986; Matsunawa et al., 1998). Ablation and its associated recoil pressure only becomes significant at extremely high power densities - exceeding 109 W/m2. Even so, the narrowness of the laser and electron beam channels calls for power densities an order of magnitude higher (i. e. 1010 W/m2). By way of comparison, an oxy-acetylene flame can achieve a power density of about 1 x 107 W/m2 (Jarvis, 2001) and GMA and GTA arcs a little over 1 x 108 W/m2 (Lancaster, 1986).

The plasma arc process (PAW) has been regarded as the only arc welding process typically operated in a keyhole mode and this has often been cited as its primary advantage over GTAW (ASM Handbook, Vol 6; Halmoy, 1994). Nevertheless, there have been descriptions of successful keyhole welding using modified GTAW equipment, for example in the dual-gas GTAW process (Norrish, 1992). In this case, however, the shielding gas arrangement has similarities to that of the PAW process in that it produces a strong ‘thermal pinch’ to increase the power density of the arc. PAW processes can achieve power densities of about 3 x 109 W/m2 and produce wider, lower aspect ratio keyholes than the laser and electron beam processes. It should be noted, however, that a significant portion of the pressure needed to stabilise PAW keyholes results from the mechanical impact of the plasma jet (Lancaster, 1986).

PAW keyholes must be ‘open’ to allow the venting of the arc gases. This means that the keyhole must extend all the way through to the root face. The plasma escaping from the bottom of the keyhole is referred to as the ‘efflux’ plasma.

3.4.3 The GTAW keyhole

With the possible exception cited above, GTAW is believed to be incapable of delivering the power densities required to generate appreciable recoil pressures (Lancaster, 1986). Keyhole GTAW has not received significant scrutiny in the literature as yet, and therefore the dominating mechanism has not been widely debated. Nevertheless, it is theorised that these low aspect ratio keyholes (aspect ratios are often less than one) are stabilised by surface tension. This being the case, it can be argued that arc pressure alone is sufficient to establish and maintain the keyhole (Jarvis, 2001). The proposed model predicts that if the keyhole surfaces could be accurately reconstructed they would be found to be closely related to minimal surfaces, familiar in such phenomena as soap films.

To begin, consider the link between surface tension and pressure. The pressure, P, across a liquid surface due to the surface tension is related to the surface curvature and can be written in the following form (Laplace’s equation):

In this expression r1 and r2 are the principal radii of curvature.

Principal axes may be chosen arbitrarily provided only that they are orthogonal and tangent to the surface at the chosen point. This is due to a result from geometry that states that ‘at any point on any surface the sum of the reciprocals of the radii of curvature in any two mutually perpendicular sections is constant’ (Grimsehl, 1947). Furthermore, the sum of the two reciprocals is called the total curvature of the surface at that point. If this result is applied to Laplace’s equation (above) then, ‘the normal pressure due to surface tension at any point on a surface is equal to the product of surface tension and total curvature’ (Grimsehl, 1947). That is, if K signifies total curvature then

[3.9]

and

P = gK

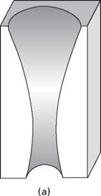
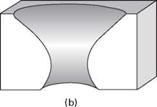
In general the two radii need not be of similar value, or even of the same sign. For illustration, if the surface is cylindrical, one radius will be infinite and can be ignored, (and K = 1/r) as is often the case in laser and electron beam keyholes. Alternatively if the surface is spherical, as in a bubble, both radii are equal (and K = 2/r). Both cylindrical and spherical surfaces will collapse unless there is a counteracting pressure because in these cases the curvature can never be zero. However, it is also possible for a surface to be concave along one axis and convex along another, that is, r1 and r2 have opposing signs. The resultant pressure change across the surface then may be positive, negative or zero. If the net pressure change is zero, the surface will be stable. Furthermore, if surface tension is the only force acting then the surface will be a ‘minimal surface’. As can be anticipated from Fig. 3.18, the stability of this type of surface is dependent on its aspect ratio.

If one is dealing with a free surface then there is no net force acting anywhere over the surface, i. e.,

gK + pgz + Parc + Pinertial + . . . = 0

where z is the distance below the pool surface, Parc is the arc pressure, Pinertial is a pressure that might be anticipated in a moving weld pool and so on. (Note that in the application of this equation care must be exercised in determining the signs of the various terms).

Since such free surfaces have not been widely discussed in relation to welding it is useful to look a little more closely at the details.

(c)

3.18 Schematic illustration of how the two radii of curvature identified in the text vary with aspect ratio. Only (b) is expected to be stable.

Potential for surface tension stabilised keyholes

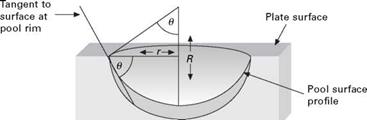
To illustrate the problem, consider the simplified system of a stationary, axi - symmetric arc and pool. Let the surface be described in cylindrical co­ordinates. Put z = 0 at the surface of the plate, with z decreasing with depth. Further, let the pool surface make an angle 9 with the radial vector (See Fig. 3.19).

Now the vertical force due to surface tension acting on the surface at a radius r is

F = g2pr sin 9 [3.12]

In order that there is no net force acting on the surface, except at the boundaries, the change in F over the annulus between the two radii, r and r + dr, must equal the vertical component of force due to all other pressure terms (P(r)) over the same area. Thus:

2pgd(r sin 9) = 2p r P(r)dr [3.13]

This gives the differential equation of the surface

-d (r sin 9) = [3.14]

It is now convenient to express sin 9 in terms of z' (= dz/dr):

sin 9 = , z' [3.15]

VT+ z'

An important mathematical case arises when P(r) is set to zero. (In welding this would be related to the improbable situation in which the arc and hydrostatic pressures are everywhere in balance).

Setting P(r) to zero and integrating once gives

rz— = c [3.17]

vttz72

Which on solving for z' gives

z' = , c [3.18]

V( r2 - c2)

If c = 0, the solution is z = constant. This corresponds to a flat weld pool and is of little interest. However, if c П 0 then the solution is

z = c cosh-1 ^cj + d [3.19]

where d is another constant of integration. Rearranging to make r the dependent variable:

r = c cosh (cd) [3.20]

This is the equation of a catenoid (see Fig. 3.20). This solution is particularly important because it can be regarded as a ‘surface tension stabilised keyhole’ and therefore supports the notion of keyhole solutions for weld pool surfaces. In practical terms it is supposed that a depressed pool surface becomes stabilised when it is pushed deeply enough to attach to the root face and rupture, creating an opening from the front to root faces.

If equation [3.16] is rearranged to represent pure pressure terms on each side

rz

= P (r)

+ z'2 J

Then one finds from [3.10] that the surface curvature (K) of an axi-symmetric surface can be expressed as

Alternatively, the curvature can be determined using the more general methods of the calculus of variations (Jarvis, 2001). This approach reproduces the above expression, or, if z is made the independent variable,

The work that has been done to date has clearly established that keyhole solutions do exist for much more realistic approximations to certain GTA welding situations (Jarvis, 2001). However, considerably more effort is required to extend these results to situations involving complexities such as reduced symmetry, metal flow and arc-weld pool interactions.

An interesting aspect of these propositions is that keyhole generation involves the transition through fundamentally different surface geometries. When the weld pool is significantly depressed, but not in a keyhole mode, surface tension acts to resist the deformation and the pool can be quite unstable. Once the surface is ruptured, forming an opening between the top and root surfaces of the plate, surface tension can drive the pool to a very stable keyhole geometry (see Fig. 3.21). One result is that the process may exhibit some hysteresis. This means that a keyhole may not form until the welding current is raised to a threshold value, but once formed it may remain open even if the current is reduced below the threshold.

An extension of the keyhole concept may offer an explanation for certain types of porosity, including tunnel porosity, that are a common defect in high current GTA welding (Jarvis, 2001). Keyhole surfaces may also generate potentially strong driving forces for (and coupling with) metal flow, as argued in Section 3.2.3. In light of these various possibilities it would appear that the study of free surface behaviour could be a fruitful area for welding science.