Моделирование миграции подземных вод
Пространственно-временная дискретизация
Кардинальной проблемой численного моделирования миграционных процессов является дискретизация в пространстве и во времени. При пространственной дискретизации наиболее часто употребляются метод конечных разностей (МКР) и метод конечных эле-
А
|
08 "т^ о7 06
02 д-Ц>. ОЗ о4 |
•Jj [сГ>
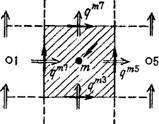
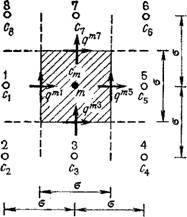
Рис. 24. Схема квадратной ячейки сеточной модели миграционного потока:
■а — параметры свойств; б — результаты миграционного расчета. / — первичные результаты; 2 — билинейная интерполяция; 3 к 4 — расчетный и соседние узлы сеткн.
Ментов (МКЭ), основные положення которых описаны, например, в работах [32, 43, 53, 72]. В дальнейшем будем рассматривать только МКР, позволяющий более наглядно представить разностную модель процесса. При этом используются консервативные разностные схемы, в основе которых находится составление баланса вещества в блоке (ячейке), относящемся к каждой узловой точке (метод составных ячеек [2, 53]).
При этом для каждой ячейки определяют конвективные притоки и оттоки мигрантов при помощи линейной интерполяции между •соседними узлами (что соответствует основной разности МКР) или используют значение концентраций с узла, из которого поступает мигрант (что соответствует обратной разности МКР). Для определения притока и оттока мигранта вследствие дисперсии используются также первые частные производные концентрации с перпендикулярно и параллельно границам ячеек, которые можно билинейно установить по соседним значениям.
Рассмотрим основные положения решения проблемы дискретизации применительно к двумерному конвективно-дисперсионному потоку в гомогенной среде с учетом процессов распада по уравнению (3.8) при Кос—Я и действия миграционных источников-стоков с интенсивностью w. В таком случае дифференциальное уравнение конвективно-диффузионного переноса нейтрального мигранта в двумерном потоке (с координатами xt при хх=х и х2—у) имеет вид
TOC \o "1-3" \h \z д / г\ дс \ , де і, дс,, ,,
-- ID,------ І + ^і------------ ас 4- w = л0 -— . (7.1)
|
|
Dxt \ ' dxt} 1 дхі 0 dt к '
Запишем это уравнение в конечно-разностной форме при квадратной сетке с шагом а для ячейки (блока) номера т, если восемь соседних узлов (ячеек) пронумеровать от 1 до 8 (рис. 24):
\qmic1 + qm3cs — qmbcm — qmlcm] о - f-
Конвективный перенос
|
Cm — c5 |
|
ОтЪ Xx |
|
Т rjml Xy |
|
Dml Хх |
|
+ |
Cg + C3-C&-—
4o
Дясперсивный перенос
_ Г),п5 C3 + Ci~C1 — C6 nmS^—Cm j_ r>m3 + —.
4a ^ УУ а 4a
|
Дсп |
|
Пи" £я УУ |
|
Firnl, yx |
|
4a |
|
Дясперсивный перенос |
Зисперснвный перенос С\Л-Ч — сь — e6
A — —« — з - f cwm. 0 dt m
Разложе- источники - ние стоки
Если знак q выявляется только в результате расчета, то в общем справедливо соотношение
2qmkc _ (gtnk _J_ gmk) ck _J_ (qtnk _ [ qmk I )
Таким образом, получают линейную систему уравнений с п уравнениями (л — число ячеек с определяемыми значениями с), асимметричная матрица коэффициентов которых указывает на каждые четыре занятых верхних и нижних кодиагонала наряду с основными диагоналями. Изображаемые таким способом вычислительные модели миграции примерно равнозначны моделям (матричным уравнениям), сформулированным с помощью нормального МКР, а также моделям МК. Э с помощью линейной аппроксимации функций. Преимущество такой системы состоит в том, что здесь гарантируется максимальная наглядность математического описания процесса.
В настоящее время при численном моделировании миграции почти исключительно используют для временной производной частную разность первого порядка и строят модель миграции, учитывая важность двух временных уровней. Тогда уравнение (7.1) для миграционной модели имеет вид
|
Де |
|
Дхі |
|
|
|
|
П-1
|
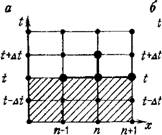
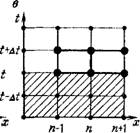
Рис. 25. Различные разностные схемы по времени. Схемы: а — явная; б — неявная; в — явяо-неявная; г — преднктор-корректор; д — временной аппроксимации третьего порядка; е — Стояяа (заштрихована область известных решении) |
Неявная (см. рис. 25, б); у=\/2— Кранка — Никольсона (см. рис. 25, в); 7=2/3 — Галеркина (см. рис. 25, в).
Для Vе (0; 2/3; 1) доказывается порядок аппроксимации 0(Д0 и для y=: 1/2—0 (Дt)[11], Из разложения функций в ряд Тейлора следует, что численную дисперсию вызывают как
Требует тонкой дискретизации. Даже обеспечение возможности коррекции коэффициента дисперсии DKop согласно выражению
TOC \o "1-3" \h \z Асор = D - [ I * I Д*/2 + А^2/(2я0)] > 0 (7:6)
Не исключает значительных затрат по дискретизации^ Для характеристики дискретизации процессов миграции пользуются безмерными числами, получаемыми из уравнения (7.3):
|
Дхі |
0 I v I Ах Ах Дtv* At I v I Редх = -—! ж и Di
D a n0D n0bl
А для характеристики осцилляций — производными характеристиками
= Л „ (7.7)
РеЛд: П0 Ах Ах П0 Ах2
Из уравнения следует, что значительные затраты на пространственную дискретизацию миграционных процессов оправданы лишь, когда одинаковый порядок величин имеет также погрешность временной дискретизации. Поэтому схема Крайка—Николь - сона с погрешностью порядка At2 часто используется в моделировании, несмотря на связанные с этим опасения в отношении стабильности. Ее повышение достигается с помощью метода «предиктор—корректор» Г10]. При этом согласно неявной схеме решения (Y=1) рассчитывается полушаг At/2 при исходном положении всех параметров ко времени t и определяются значения с*+Л(12. Затем по схеме Крайка—Никольсона (у= 1/2) реализуется весь шаг At, причем все параметры миграции, члены источников-стоков, обмена и замещения, а также член конвекции задаются на момент времени t+At/2. Таким образом, вычислительная модель уравнения (7.2) при полном шаге получается в таком виде (см. рис. 25):
» In дс "llV 1 Г * (п дс "il^j-L і/.
J+At_ t
At
Нередко оказывается успешным использование для временной дискретизации конечно-разностной аппроксимации третьего порядка 0(^3):
Де / 2<?+л* + гс<+<*~2ЛІ
Dt / 6Д*
При этом практически не требуется дополнительных затрат на расчеты, но остается потребность в месте накопления данных. Аппроксимация третьего порядка 0(Р), образованная для схемы 122
Кранка — Никольсона [см. уравнение (7.2)], получается согласно [55] в виде
|
Дс М &*с |
|
(7.8) |
|
М ~ 2 |
|
Dt 6 дР |
Dt дjr. + dt ■
Д t
Если в это уравнение, согласно порядку аппроксимации, подставить c=t\ то получают [ (И-Д/)3—Р]/Д*=За^ (^-f-AO 2+6а2(/+ откуда следуют уравнения для определения коэффициентов 6а,/а=3*а, бщіМ+бщі+ба^Зт, За, А^2+ +6а2Д*=Д*2, что дает ^=0,5, а2= — М/12, а3 = + At/12. Тогда
Дс____ дЬТУ+М
Dt 6 дР J +2
Причем для dc/dt надо подставить одно-, дву - или трехмерное исходное .дифференциальное уравнение, а для d2c/dt2 его производную. Наконец, очень значительная точность аппроксимации достигается благодаря тому, что временная производная учитывается не только в точке п (это в общем виде относится также к членам источников-стоков ic и да), но и на соседних узлах. В наиболее простой форме эту подстановку осуществляют по правилу Симп - сона: dc/dt-(1/6) [{dc/dt)a-.i+4(dc/dt)n+(dc/di)n-1].
На рис. 25, е приведена также конечно-разностная схема для одномерных процессов миграции, предложенная Г. Стояном. Эта схема дает возможность управлять вычислением всех частных производных и получать стабильные и точные численные решения, особенно для случаев чистой дисперсии или чистой конвекции.
Выбранный численный метод пригоден лишь в тех случаях, когда численное решение стремится к точному при уменьшающейся ширине. шага, т. е. когда этот метод является сходящимся.
Численная дисперсия вызывается прежде всего дискретностью членов:конвекции и емкости (аккумуляции), т. е. первыми производными зависимых переменных. Это может приводить к значительным погрешностям при моделировании миграционных процессов с? небольшим коэффициентом дисперсии £>, величина которых для различных численных моделей миграции получается в зависимости от Ре^лг и числа Di или Сг. Благодаря введению исправ< ленных. коэффициентов дисперсии [см., например, уравнение (7.6)] значительно уменьшаются погрешности и в простых дискретных схемах. (Стабильные обратные разности членов конвекции и аккумуляции, а также МК. Э с линейными пространственными и временными начальными функциями приводят к значительной численной дисперсии или требуют очень тонкой локальной и временной дискретизации.
Численные осцилляции происходят в определенных условиях и, как правило, определяются сравнением с соответствующими аналитическими решениями. Опасность колебаний возникает преимущественно в процессах с доминирующей конвекцией. Особенно подвержены осцилляциям схема Кранка—Никольсона, основная разность членов конвекции или аккумуляции и формулировка МКЭ
по схеме Галеркина с линейными функциями. Вместе с тем неявная схема, обратные разности членов конвекции и аккумуляции, а также формулировка МК. Э по Ритцу и по Галеркину с многократной коллокацией в значительной мере свободны от осцилля - ций. Вместе с тем чем «нейтральнее» численная схема, тем она точнее и чувствительнее к нарушениям. Поэтому применяемая на практике численная схема постоянно является компромиссом между обеими тенденциями.
Наряду с погрешностями дискретности имеют значение также погрешности в стабильности, вытекающие из ограниченного количества численных расчетов. Безусловно стабильной считается численная модель миграции, если численная погрешность (округления) уменьшается от одного временного шага к другому, а условно стабильной — если это происходит только при определенных условиях. Эти условия для особых случаев аналитически представлены в работе [50]. Таким образом, сравнением с аналитическими решениями фиксируется условие стабильности при заданной пространственной дискретизации путем установления критической величины временного шага через критические числа Di или Сг. Безусловно стабильной является неявная схема решения с у—1, причем с уменьшением у возрастает склонность к нестабильности. Численное решение составленной системы уравнений (матричное уравнение) также таит в себе возможности погрешностей. К очень большим погрешностям, сильно распространяющимся при условном стабильном методе, может приводить решение системы уравнений с плохо выраженными условиями, у которых элементы основных диагоналей матрицы коэффициентов в недостаточной степени преобладают по сравнению с основными диагоналями кодиа - гоналей.
Значительные погрешности в решении уравнений может вызывать решение всей системы уравнений с помощью частного метода шагов (например, неявного метода переменных направлений) и переноса элементов матрицы коэффициентов в правую ч"асть уравнений путем умножения на временные или итеративно зависимые переменные с обратной датировкой для создания ленточных матриц с незначительной шириной ленты (преимущественно тридиаго - нальные матрицы коэффициентов). По этой причине следует тщательно проверять и контролировать программы компьютера па численному моделированию миграции, особенно путем сравнения с аналитическими решениями.
На основе численного решения производится первичное определение числа опорных точек в пространственно-временной сетке. Число опорных точек по времени или по размеру итерационного шага при нелинейном решении указывает количество определяемых локально-дискретных значений зависимых переменных (Я или иногда vx, vy, с) и таким образом влияет на число уравнений системы. Затраты времени на одноразовое решение этой системы уравнений являются основной величиной для оценки затрат; они зависят от типа ЭВМ, используемого метода для решения системы 124 уравнений и качества генерированной вычислительной программы. Если эти затраты умножить на число временных или итерационных шагов, необходимых для моделирования, и прибавить к этому затраты времени на корректирование матриц коэффициентов и правой стороны уравнений, то получится время, необходимое для математического моделирования на ЭВМ. Потребность в месте накопителей для математического моделирования многомерных процессов миграции определяется прежде всего потребностью в месте накопления подпрограммы для решения системы уравнений.