разное

Основные понятия блока «вещество»

В холодильной и теплонасосной технике в качестве источников тепла рассматривают тела, которые характеризуются ограниченностью размеров (!) и чаще T^onst. В этом случае термодинамической характеристикой выступает теплоемкость.

Теплоемкость - это количество тепла, подведенное (отведенное) к телу ограниченных размеров при соответствующем изменении температуры этого тела
где х - указатель типа и характера процесса (х =р соответствует изобарной теплоемкости; jc=v - изохорной теплоемкости).

Поскольку количество поглощенного тепла зависит от характера процесса, то и теплоемкость определяется характером этого процесса. Любая термодинамическая система имеет множество значений теплоемкостей в зависимости от вида процесса, в связи с чем численное значение теплоемкости в общем случае может изменяться в пределах от до Для практического использования интерес представляют изобарная (Ср) и изохорная теплоемкости (Cv).

По Первому закону термодинамики

SQ - dU - ь pdV.

Если выбрать Т и V независимыми переменными, то U=U(T, V). Запишем полный дифференциал для U=U(T, V)

(2.35)

Подставляя ур.(2.35) в выражение для 8Q, получим

Ди_\ dv)T

Аналогично, выбирая независимыми переменными Тир, получим

Из yp.(2.36) для изохорного процесса dV=0 получим изохорную теплоемкость

Из yp. (2.37) для изобарного процесса dp=0 получим изобарную теплоемкость

Т =т +рт

DT)p UT)P

Разность теплоемкостей составит

Второй член в правой части ур. (2.39) для Ср описывает эффект, оказываемый работой, которая совершается во время расширения газа (при p=const) при поглощении тепла SQ. Аналогичный член отсутствует в ур. (2.38) для Су, так как в данном случае объем остается постоянным (V=const), т. е. не происходит расширения.

Для элементарных равновесных процессов выражение Первого закона термодинамики (для идеального газа) принимает вид

SQ =CydT + pdV.

Продифференцируем уравнение состояния для одного моля идеального газа pV=RT

PdV + Vdp = RdT.

Подставляя его в ур.(2.41), получаем уравнение для одного моля идеального газа

(cv+R)dT - Vdp = SQ,

При р—const

■cv +R

Или

Ср - Су = R.

Таким образом мы получили уравнение, известное как уравнение Майера, которое читается следующим образом: удельная молярная теплоемкость идеального газа при постоянном давлении превышает его удельную молярную теплоемкость при постоянном объеме на величину универсальной газовой постоянной.

Рассмотрим приток тепла в систему при р-const

DQ = dU + dW

Или

= U2-U,-p(V2-V1),

Тогда

H1=U1+pVl H2 =u2 + pV2

AQp=comt =H2~H1-

■p=const

Энтальпия[1] (H=U+pV) - инженерная функция, введенная для удобства пользования таблицами и диаграммами состояния рабочих веществ при проведении расчетов.

Свойством рабочего тела называется любая измеряемая характеристика. Прямым замером можно определить температуру, давление, объем. Остальные свойства рабочего тела можно получить косвенным замером, т. е. через использование аналитических выражений, в которых будут участвовать величины, полученные прямым замером.

Функция соответственных состояний для любого вещества с известным неизменным составом в любом агрегатном состоянии в общем виде записывается как

F(p, T,v) = 0,

Частный случай которой для газов представляет уравнение Менделеева-Клапейрона

P-V=MRT.

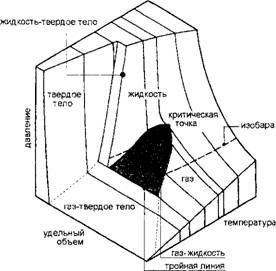
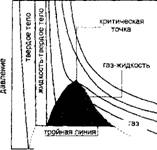
В общем виде диаграмма состояния рабочего вещества представляет поверхность в координатах p-T-v (рис.2.5). Для простоты использования, эта диаграмма перестроена по каждой из трех плоскостей проекции. Для инженерных и научных расчетов построены и применяются диаграммы: T-s, p-v, T-v, p-h, s-h, а также любые другие.

Любое вещество может существовать в трех агрегатных состояниях: газ, жидкость, твердое тело. Условие одновременного существования трех фаз на диаграмме состояний называют тройной точкой.

Б)