МИКРО ПЛАЗМЕННАЯ СВАРКА

ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ СТОЛБА ЦИЛИНДРИЧЕСКОЙ ДУГИ

Ранее известные численные решения уравнения (1.3) выполня­лись, как правило, при значительных упрощениях. В ряде работ принималось, что коэффициент теплопроводности X не зависит от температуры. В других работах зїа зависимость задавалась в виде степенной функции. Причем во всех случаях решение выполнялось без учета электронной компоненты теплопровод­ности плазмы.

Численное решение уравнения баланса энергии (1.3) в на­стоящем изложении выполнено [15] с учетом электронной и атомной теплопроводностей плазмы как функций температуры, а также с учетом электрон-атомиых и электрон-иошшх взаимо­действий при вычислении электропроводности плазмы. При этом в соответствии с результатами анализа экспериментальных дан­ных и постановки по уравнению (1.3) вариационной задачи на отыскание минимума энергии столба дуги значение напря­женности электрического поля принималось не зависящим от координаты г в любом поперечном сечении столба.

Решение уравнения (1.3) проводилось методом Рунге— Кутта

с/7*

на ЭВМ «Минск-22 Л1!». Для заданных граничных условий =0

численные значения температуры Т (г) сравнивались с законом нормального распределения

Т (г) = 7> ех р (—&2г2), (1.4)

где Ь2—функциональный коэффициент, зависящий от состава среды и режима горения дуги.

Все результаты вычислений выводились на печать в виде таблиц для г, Т (г)/Г0 и / (г)//0 в каждой строке через Дг = 0,1 мм В таблице печатались также исходные данные: V*, Го, х и и некоторые результаты вычислений: £, 1ВЫЧ. Отметим, что зна­чение To = f(lp) задавалось в виде массива, заимствованного из экспериментальных данных. Типичная таблица для дуги, го­рящей в смеси 90%Аг+10%Н2, приведена выше (табл. 2). Из данных таблицы видно, что с увеличением координаты г плот­ность j (г) быстро падает. Температура же снижается медленнее, и в области, где j(r)/jo практически равно нулю, значение тем­пературы Т (г)/Го~0,61 -=-0,63.

Вычисления показали, что коэффициент Ь2 в исследованном диапазоне изменения г является практически постоянной вели­чиной. Это свидетельствует о том, что радиальное распределе­ние температуры достаточно хорошо описывается нормальным законом Гаусса, т. е. формулой (1.4).

Рис. 2.

Радиальное распределение температуры (/) и плотности тока (2) для смеси 90% Аг+ + Ю% Н2:

= 11,5 А/мм2, b2 =*а 0,55 мм 2*

миг*2, с4 — 1,31мм““4, а2 =4,53 мм 2»

6 — /д = 22.5 А, /0 = 7 А/ММ*. Ь2 = 0,13 мм*-2,

= 0,696 вш 2, с* *= 0.172 мм о2 = 0.983 мм—2»

о— /д = 50 А, /о = 8,1 А/мм2. Ь2 =» 0,07 мм 2, с2 ^=*0,231 мм~2, <г4 = 0,068 мм о2 = 0,453 мм““2-

Типичные кривые распределения температуры и плотности тока для различных значений ток* дуги изображены на рис. 2. Там же в виде крестиков нанесены значения Т (г)Пq, вычислен­ные но уравнению (1.4). Плотность тока /(г)//о более сложно Умнисит от радиуса, но в большинстве случаев может быть опи­тна зависимостью типа

/ (О = /о ехр [— (аУ

где а и с — коэффициенты, определяющие степень сосредото­ченности тока дуги.

Значения / (г)//о» вычисленные согласно выражению (1.5), по­казаны точками. Легко видеть, что при соответствующем выборе

коэффициентов а и с4 результаты численного решения уравнения (1.3) хорошо могут быгь представлены аналитическими функ­циями.

Интегрирование выражения (1.5) позволяет установить связь между током дуги, плотностью тока на оси и коэффициентом сосредоточенности тока:

71/о ъЕо Vl)

J2

а

где

а.

— коэффициент сосредоточенности тока эквивалентного гауссов­ского распределения (коэффициент контрагирования столба дуги),

/' (г) = /о exp (—а2/-*), (1.8)

/2 с

/ [ —гг І — сложная аналитическая функция, график которой изобра-

ai /

жен на рис. 3.

Таким образом, выражение (L5) можно заменить эквивалент­ным нормальным распределением (1.8) с коэффициентом я2, ко­торый легко определить с помощью коэффициентов Cl и с и рис. 3. При этом нормальное распределение тем точнее описывает ис­
тинное распределение (1.5), чем меньше ток дуги. Коэффициент а2 ье зависит от координаты г. Из рис. 3 видно, что при с2 О коэффициент а2 а.

Замена формулы (1.6) выражением (1.8) приводит к неко­торой неточности в определении радиуса токового канала стол­ба. В центральной части столба распределение j(r) идет ниже (рис. 2, штриховая кривая) истинного (кривая 2), а у грани­цы— выше. В связи с этим условие /(/?)//0===0,005, опреде­ляющее границу токового канала при вычислении j(r) наЭВМ„ для гзуссовского распределения преобразуется в j(R)/j0^0y03~ -4-0,05. Поэтому условный радиус токового канала по формуле

(1.8) определяется как

(19>

а

С другой стороны, по значению температуры на границе то­кового канала из формулы (1-4) находим b2R2 — 0,5. Объединяя равенства относительно R2, получаем

д2^ (6-~7) Ь2У (1.10)

т. е. коэффициент контрагирования аг может быть определен через коэффициент температурного распределения b2.

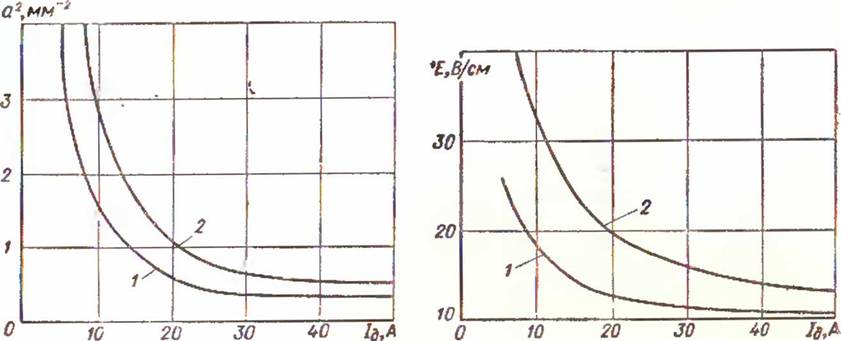
Зависимость а2 = 7Ь2 — /(/д), вычисленная на ЭВМ для ду­ги, горящей в аргоне и смеси (90% Аг+,10% Н2), показана

Рис. 4.

Зависимость коэффициента контрагирования от тока дуги:

аргон: 2 — смссъ 90% Аг - f. 10% H*.

на рис. 4. С ростом тока коэффициент сосредоточенности пада­ет. Увеличение коэффициента теплопроводности газа Уа (на­пример, за счет добавки водорода к аргону) ьедет к увеличению ■коэффициента сосредоточенности тока, а следовательно, и к уве­личению степени сжатия дуги. Усиление сжатия столба вслед­ствие добавки водорода особень^ заметно в области малых токов. При больших токах кривые а2=}(1я) для различных значений Уа сходятся достаточно близко, что свидетельствует об ослаблении влияния среды на контрагирование дуги на боль­ших токах. При малых токах /д < 20 А можно управлять «фо­кусировкой» дуги, влияя на среду посредством коэффициента XG. Естественно заключить, что чем больше коэффициент теп­лопроводности газа, тем острее будет сфокусирована дуга. Это явление использовано пр. и разработке микроплазменной сварки металлов малых толщин.

Из формулы (1.6) видно, что для заданных значений /д, Vi, То напряженность электрического поля растет с увеличением коэффициента сосредоточенности тока. Поэтому коэффициент теплопроводности газа Уа существенно влияет на напряжен­ность электрического поля и на вольт-амперную характеристику E-f(I^) столба (рис. 5). С ростом Ха электрическое поле уве­личивается. Данная зависимость является иллюстрацией хоро­шо известного экспериментального факта, что всякое улучшение теплообмена между столбом дуги и окружающей средой ведет к рос і у напряженности электрического полм и сжатию дуги. При малых токах напряженность поля резко зависит как от со­става среды, так и от величины тока. С увеличением тока зави­симость E=f(In) ослабляется и, начиная с /Д=15-~20А, прак­тически не зависит от тока. Зависимость Е от состава среды •сохраняется: большему значению Хс соответствует более высо­кое значение поля Е. Эта закономерность также хорошо согла­суется с данными экспериментов. Следовательно, рассчитанная ъольт-амперная характеристика столба находится в хорошем соответствии с экспериментальной как по диапазону, так и по темпу. изменения переменной величины.

Изложенные расчеты позволяют получить радиальное рас­пределение температуры и плотности тока в столбе дуги, вы­числить напряженность электрического поля и коэффициент сосредоточенности тока в зависимости от свойств среды и тока дуги. Результаты расчетов хорошо согласуются с эксперимен­тальными данными. Таким образом, изменяя теплофизические свойства среды, можно управлять энергетическими параметрами малоамперной дуги при сварке.

Способ получения сжатой дуги и ее применение