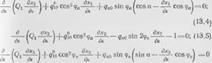Механика трубопроводов и шлангов

Основные результаты экспериментальных исследований взаимодействия плохообтекаемых профилей с потоком

Исследование статики стержней некруглого сечения (см рис. 11.1) невозможно без экспериментального определения за­висимости аэродинамических коэффициентов от угла атаки аа, который в процессе нагружения стержня аэродинамическими си­лами непрерывно изменяется. Если для стержня круглого еече - иня аэродинамические коэффициенты в определенных интерва­лах чисел Рейнольдса (что эквивалентно определенному интер­валу скорости потока) можно считать неизменными, то для стержней некруглого сечения аэродинамические коэффициенты непрерывно зависят от скорости потока из-за деформаций, стержня, непрерывно изменяющих местный угол атаки аа. Как уже указывалось во введении, основная цель данной книги за­ключается в изложении прикладных методов решения задач статики и динамики стержней, взаимодействующих с потоком (внешним и внутренним) воздуха или жидкости, поэтому при­ведем результаты экспериментальных исследований взаимодей­ствия стержней некруглого сечения с потоком в объеме, необхо­димом для решения уравнений равновесия. Экспериментальные исследования обтекания стержней некруглого сечения проводи­лись рядом авторов [24, 26, 44]. Воспользуемся результатами экспериментальных исследований, приведенными в работах [32, 36].

Изложенные в данной монографии методы исследования взаимодействия гибких стержней и нитей с потоком воздуха или жидкости могут быть использованы для проведения стати­ческого н динамического анализа поведения гибких элементов конструкций в потоке при условии, что имеется необходимая для расчетов информация о аэродинамических силах. Для раз­работки алгоритмов решения предположения о том, что дейст­вующие на систему силы известны достаточно. Однако для по­лучения числовых значений, близких к реальным, при решении уравнений равновесия нли движения, требуется, чтобы числовые значения аэродинамических сил соответствовали реальным

Значениям в каждом конкрет­ном случае для любого профи­ля стержня (в том числе и для плохообтекаемых профилей).

В этом основная трудность всех аэроупругих задач, так как получение подробной и до­стоверной информации о силах («входе») — несоизмеримо бо­лее сложная задача, требую - Рис‘ 12,1 щая очень большого объема

Экспериментальных исследований, чем последующее решение уравнений движения. Достоверность результатов решения урав­нений движения полностью зависит от достоверности принятых в расчете аэродинамических сил. Основная трудность при опре­делении аэродинамических сил, действующих на стержень с пло­хообтекаемым профилем, заключается в том, что аэродинами­ческие коэффициенты сп, съ и ст (ст — коэффициент аэродина­мического момента) очень чувствительны к углу атаки, причем ^та зависимость нелинейная и в свою очередь зависит от ори­ентации главных осей сечения стержня по отношению к направ­лению потока (рис. 12.1). Для решения уравнений движения не­обходимо иметь аналитическую зависимость аэродинамических коэффициентов от угла атаки аа, которую можно получить толь­ко при обработке результатов экспериментальных исследований, например воспользовавшись теорией сплайн-функций [2].

Результаты экспериментального определения коэффициентов аэродинамических снл указывают на существенную зависимость коэффициентов сп, Сь и ст от формы поперечного сечения стерж­ня, обтекаемого потоком его ориентации по отношению к потоку п целого ряда других факторов, например степени турбулентно­сти потока, качества поверхности обтекаемого элемента конст­рукции (коэффициента шероховатости) и т. д. Информация о значениях коэффициентов аэродинамических сил и нх зависимо­сти от перечисленных параметров в каждом конкретном случае может быть получена только экспериментальным путем.

В данном параграфе приводятся результаты эксперименталь­ных исследований, целью которых было определение коэффици­ента аэродинамических сил (силы лобового сопротивления, бо­ковой и подъемной сил), критических значений параметров по­тока (скорости и направления), а также влияния турбулентно­сти. моделей на величины аэродинамических нагрузок, действую­щих на гибкие стержни с различной формой поперечного се­чения.

Ограничимся основными результатами экспериментальных исследований, опуская описание экспериментальной техники и методики проведения испытаний, которые подробно изложены в ряде книг, например [24, 26].

' аэродинамические силы и моменты, модули которых равны:

<]п=-~с„ р*|; (12.1)

Ы=4-е,

Входят аэродинамические коэффициенты сп, сх, и ст> зависящие от угла атаки аа. Для частного случая обтекания цилиндриче­ских тел (стержней) некруглого поперечного сечения при ао=0 (при этом условии Сь=ст=0) подробная информация о коэф­фициенте сп силы лобового сопротивления содержится в книге [24]. При экспериментальных исследованиях [26, 44] рассматри­вались сечения, приведенные на рис. 12.2 (6 = 9 см, а= 18 см, /=30 см). На рис. 12.1 показано прямоугольное сечение стерж­ня (рис. 12.2 сечение //) при произвольном положении главных осей сечения по отношению к направлению потока (эксперимен­тальные исследования проведены И. Ю. Графским и М. И. Каза­кевичем).

На рис. 12.3 представлены графики зависимости аэродинами­ческих коэффициентов сп и сх. от угла атаки аа для сечения I: х, у — оси поточной системы координат; дп, дь — соответст­венно сила лобового сопротив­ления и подъемная сила. Кри­вые этих зависимостей полу­чены при скорости потока, 26 м/с. Графики зависимости аэродинамического коэффици­ента подъемной силы от скоро­сти потока (числа Рейнольд­са) при различной его турбу­лентности и шероховатости поверхности сечения / для зна­чения угла атаки аа=22,5° да­ны на рис. 2.4 для разной сте-

Пени_ турбулентности потока ет при коэффициенте шероховато­сти к=10-2. На рис. 12.5 приведены экспериментальные зависи­мое гп для коэффициента подъемной силы (при «с=29,50) для к=10-4.

Графики зависимости аэродинамических коэффициентов силы лобового сопротивления с«, подъемной силы сь и осевого момеи - та ст от угла атаки аа для сечения II даны на рис. (12.6). Кри­вые 1, 3, 5 соответствуют значениям аэродинамических коэффи­циентов, полученным при турбулентности потока 8Т=0,5%, а кривые 2, 4 — при ет=8%. Испытания, результаты которых представлены на рис 12.6 проводились при скорости потока в рабочей части аэродинамической трубы 25 м/с.

На рис. 12.7 приведены графики изменения аэродинамичес­ких коэффициентов с л, ci и ст в зависимости от аа для сечения III при скорости потока i'o=5 м/с, коэффициенте шероховатости к=9-10-5 и степени турбулентности потока ет=0,5%. Из графи­ков следует, ЧТО коэффициент подъемной СИЛЫ Cl, очень сильно изменяется в зависимости от аа.

§ 13. Уравнения равновесия стержня в потоке

Получим уравнения равновесия стержня круглого поперечно­го сечения в потоке при больших перемещениях (нелинейные уравнения). В этом случае можно считать, что в потоке на стержень действуют только распределенные аэродинамические силы qaxi, а аэродинамические моменты [Нэсг - = 0- Уравнения рав­новесия стержня в потоке полностью совпадают с уравнениями равновесия трубопроводов (7.1) — (7.3) или (7.72)—(7.74), в ко­торые вместо qG надо подставить полученные в § 11 аэродина­мические силы qn и qr. Аэродинамические силы входят тольке ■ в уравнения равновесия сил. Остальные уравнения, характери­зующие состояния равновесия стержня, от аэродинамических сил не зависят.

Ограничимся подробной записью только уравнений равнове­сия сил, которые, например, в проекциях на неподвижные оси имеют вид (при P(ij=0)

TOC o "1-5" h z дО„ п / Л*,

—^-+?10 COS2'fa—e—-Qno Sin <pe (cos a----------- cos 9a) =0; (13.1)

-^p-+9?o cos2---------------- gn0 sin 2'fa ----- 1 = 0; (13.2)

-^+Ґ°o cos2<p„-^- + ?„0 sin <pa ^sin a ^ cos<p„) = 0, (13.3)

Где coscp„=^!- cosa-i - sin a,

A ds

sin?«=>Al- cos29„.

Остальные уравнения равновесия остаются без изменения.

Численное решение нелинейных уравнений равновесия стерж­ня в потоке (двухточечной краевой задачи) является весьма гложиьщ Решение можно получить, используя метод последо­вательных нагружений (последовательно нагружая стержень малыми аэродинамическими силами) при известном начальном і'остоянии стержня. Для этого можно использовать метод, из­ложенный в книге [И]. Аналогичный метод для решения уравне­ний равновесия абсолютно гибких стержней в потоке изложен

И § 14.

Уравнения равновесия абсолютно гибкого стержня. В случае абсолютно гибкого стержня (ннти) уравнения равновесия

(13.1) — (13.3) имеют вид

(13.6)

(13.7)