Механика трубопроводов и шлангов

Численное решение нелинейных уравнений равновесия абсолютно гибких стержней, взаимодействующих с потоком

При рассмотрении равновесия нити в потоке без ограничения на смещения ннти имеем нелинейные уравнения (13.4) — (13.7), |ашение которых в замкнутой форме невозможно, поэтому оста­ются только численные методы решения с применением ЭВМ. Ниже излагается общин метод численного решения нелинейных равнений равновесия нити, позволяющий определять форму нити и натяжение при любых внешних распределенных силах и при любых - сколь угодно больших отклонениях иитн от началь­ного состояния равновесия.

В § 13 были получены уравнения равновесия нити в непо- пшжной системе координат, которые можно представить в виде

Получим выражения для малых приращений ЛлгГ и Д<$)

Первого приближения, воспользовавшись уравнениями (14.1),1

(14.2):

ДО*,’ ^-<3,,, ’ + ДО'11 ■ (Х,=х1с+Ьх1)); (14.3)

^ =0.0^+ Ад!'1 (С',(=С),,0+ДО1‘1); (14.4)

Й<г£)=<г»^->+л«1,)-^2- №1=ею+й<з("). (м.5)

.где (2ю — натяжения в нити при цах =0 (от сил веса), —ко­ординаты точек нити, характеризующие начальное состояние равновесия (до действия потока).

Для определения ХгО и Сю имеем систему уравнений

(-*зо=0); (14.6)

«о+^=»-

Решение системы (14.6) приведено в § 9.

В результате имеем следующие выражения для определения 1 «ю. -«го и <Эю:

СЛо=С' ]/1+-^ +^~ (й=С1вЬс,),

•*10 —С|/Фю» Л20 = (е -|~ Сз)/(Э 1о,

*"=5 йГЛ-

Произвольные постоянные находятся из уравнений 1-х|,=2с1(сЬ-^—1);

1=сг ^ь(-^—яЬс^; с3— — сг сЬ с2-

Нагружаем нить малыми значениями аэродинамических сил &Яах1 и на каждом шаге нагружения находим равновесную фор - 1

84

Му нити и натяжение, повторяя этот процесс до заданных значе­ний дал, равных

?„.=2 (14-7)

Где к — число нагружений.

Получим основные уравнения, необходимые для реализации изложенного метода последовательных приближений.

Подставив ^=л:ю+ДлГ{(1) в уравнение (14.2), получим (при

Дл:42=0)

2^с'-0Дл:1( ^=0; У^|0= 1. (14.8)

Умножим каждое нз уравнений (14.3) — (14.5) на х'ы и сло­жим получающиеся уравнения [с учетом соотношений (14.2)], получим

АС?{1) = АЙ?*» + ЛСЙ^+ЛЙ^зо. (14.9)

Исключим АСЫ1' из системы уравнений (14.3) — (14.5) и пре­образуем новые уравнения к виду

— [(1 — х’ы) ЛЙ1/ — лтшАГгоДф^—■*ю*£(>Д0£) 1 >

Де <2ю

|— [ — х[оХ2аЩ{к^ + (1 — *2о) Щх} — *20*30Аф^];

Де

(14.10)

Адлг(1) 1

—г~—=-—— [ — *10*30^(2^— -^о-КзоДСл^ Ц - (1 —*зо) ДЙВ]. дв Ою

Уравнещя равновесия с учетом приращений Аф^. и &дах - чринимают вид

Я, ... -£М--^-+^.=0;

+ + (14.11)

<?ф„ , дДф!1*

__^+_^+^=0, или после исключения из (14.11) уравнений равновесия нити без учета потока получаем дА0(х1)

Где р<1 — коэффициент, зависящий от выбранного шага на­гружения.

При первом приближении аэродинамические силы следует брать, зависящими от х'-0 :

B/&=яgЈ](xiп, (14.13

Например, при р=0,1

АЗax]=?qi\=0,зЈr ( 14.14}

Так как аэродинамические силы AЗaJj известны (они зави - сят от XI предыдущего приближения), то из (14.2) получаем

IQi‘>= - f V«п,* + d,)= - ACiV+a1’.

AQОv? = - ( aЖ).* + 4I)= _ дЩ’+сЁ", (14.15)

О

TOC o "1-5" h z ыQЬ’ = - j +

Выражения для AQОя дают возможность получить из систе­мы (14.10) уравнения для определения Алг/1} первого прибли - жения:

(4»_ (_ д5«.,

0® vio vio

VlO

Ф^)=_^Ј0 (_ ддО) +

ЬК VIO Vio

-■^(-АЙ?+4ч): (14.16)

Vio

(-лаа* +4ц> _^(_вej+rf*)+

Vio Qio

+ 0г^)(_дщ)+41)).

QlO

Интегрируя систему (14.16) при нулевых начальных значе - шях Аж|1,(0) от нуля до единицы, получаем систему уравнений ичя определения произвольных ПОСТОЯННЫХ ^4! Ср И Св1 гспользуя однородные краевые условия для Ал:*1* (1)=0:

Аі іс4** о-ч$ * а, А1) - Ь а=О, а21с1) а22С51)+а22сі1) а2=0; (14.17)

* Язз^б1 * а&—0»

•5 От

Л# 20 ^ <?10

<ы=-^

.) <?Ю

А,= | *ч>*а> л(п(') і -*«>■**> .піч I

І <?10 Хі п-

Определив из системы (14.17) 4^» £5!) и Л1 находим функ-

Щи Ддг/(1> и АкГ^интегрируя уравнения (14.16) от нуля до е). Определив произвольные постоянные С^К.. и Дф** получим первое приближение для &0.:

(14.19)

В результате получаем все функции первого приближения (при заданном Д^й? =0,1^п0, А^^ОЛфм)

Х1=хл + ьЯ (&г>=Яп+Ы$1'. (14.20)

Первое приближение может сильно отличаться от точного решения, поэтому, повторяя изложенный процесс (для данных д*й? и А0$)* можно получить приближение с любой заданной точностью, например, чтобы два последовательных приближения

Отличались друг от Друга не более чем на один процент, т. е. чтобы выполнялись условия

—Г°<,;

(14.21)

Получаем соотношения для последующих приближений при первом шаге по нагрузке в аэродинамических силах

Определив Ах'!** из уравнений (14.16), находим новые значения для производных:

Х'Р^х'Я+Ах'Р,

Arfl>(1}=^i^)Иl,). (14.22)

Затем находим уточненные значения (соотношения

(14.15) ). Новые значения с£1)(1), с£1>(1> и 41>(1) находятся из

Уравнений (14.17) относительно Ад:/1*(1), в которых вместо <210 и Хго следует взять их уточненные значения:

<?"’=Сю+йО(.1И1 (14.23)

Определив новые значения произвольных постоянных, нахо­дим АХ[ (е) и Ах1)^1г) из (14.16), а затем новое значение ддГИ1) ит. д.

Если на /е-й итерации получающиеся функции Ах(1)(к ^Х1 И Лр11)(К) удовлетворяют условиям (14.21), то можио переходить к следующему шагу нагружения, положив в аэроди­намических силах АЯп> —0,2?по; А^1о}=0,29?о.

Решения, соответствующие первому шагу нагружения аэро­динамическими силами, соответствуют

-к!1’=*,(,-)-Ддг!1и'!'; х'г')=хк,+ й*;“’“0;

Получаем уравнения для определения второго приближения, соответствующего удвоенной аэродинамической нагрузке (пер­вое приближение):

ДДО<2><1)

—+ Д? Д(1,=0 [й9Й»=2&&~, ' О4-25)

[§ (^ГхГ) <*««]. (14.26)

Из системы (14.15) определяем Дф^,(1):

| Д^<1,Л+сЙ/1>. (14.27)

Затем из системы (14.17) определяем произвольные постоянные с¥+1 и функции Дх/(2) и Дх*2). Определив дх;12), уточняем зна-

* (2)(1) ОС. / ' I « '(1) I А 'РН1)*

Чеиия Ьфс” *=2&1Х1 (хю+Дл:/ Дх,- /, соответствующие пер­вому приближению при удвоенных аэродинамических силах. Проделав несколько раз этот процесс итераций, получим значе­ния функций Ах! И Дх/2)(¥) и Д01* удовлетворяющие усло­виям (14 21), что соответствует полному решению исходных уравнений равновесия (при аэродинамических силах, равных 2Р? о»,):

*,=.*,О+Д^’ + Дд:!2’'*1,

/ • , . '(1)(к) ■ д /Л Л 004

Х,=Лг(о ~|” Дх/ -(- Дх > (14.28)

0,=^^+ аС>Г><К,+ до™

Повторяя этот процесс последовательных приближений, мож­но получить форму равновесия нити и натяжения при любых значениях аэродинамических сил. В аэродинамические силы вхо­дят безразмерные множители дпо и дю°, которые равны отноше­нию максимально возможных аэродинамических сил (нормаль­ной и касательной), действующих на единицу длины нити к силе тяжести единицы длины нити, поэтому, если (3=0,1, это значит, что сила лобового сопротивления (нормальная) в 10 раз мень­ше погонной силы тяжести нити. Поэтому, нагружая нить по­следовательно аэродинамическими силами (кф)дах, (^1 = 1*

2, , р), можно рассмотреть статику нити прн т. е.

Когда сила лобового сопротивления (амплитудное значение) ннти больше погони« силы тяжести нити.

Рассмотрим несколько конкретных примеров численного ре­шения нелинейных уравнений равновесия.

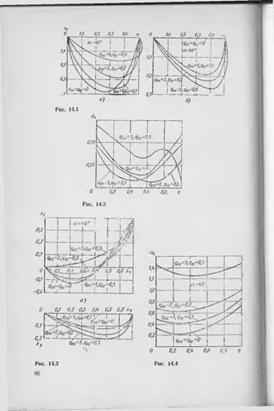
На рис. 14.3, а, б приведены проекции осевой линии стержня при х^—ОЖ, *2к~0,4 для тех же значений угла а и аэродинамических сил. Осевые усилия* соответствующие равновесным формам рисунка 14.3, показаны на рис 14.4. Из сравнения рис. 14.2 и 14.4 следует, что характер закрепления концов стерж­ня оказывает существенное значение на осевые усилия, в том числе и на их максимальные значения, что следует учитывать при расчетах.

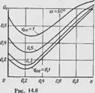
На рис. 14.5 приведены графики распределенных аэродинамических сил? при различных скоростях потока V» (различных и ^!0°, при #ю°=

=0,1 <7пг)) *1к=0,4, х2к=0,7 и а=90°. Из графиков следует, что с ростом скорости ь0 (с увеличением (/по и <?ю°) из-за отклонения нити от вертикальной плоскости проекции аэродинамической силы гу,, очень сильно изменяются как по модулю, так и по направлению, в том числе и по отношению к связанным осям. Изменение натяжения в нити для этого случая закрепления и направле­ния потока приведено на графиках рис. 14 6.