Механика гидро - и пневмоприводов
Источник энергопитания с автоматически регулируемым насосом
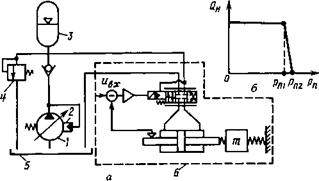
Для уменьшения затрат энергии, которые могут быть значительными при использовании переливных клапанов, применяют источники энергопитания с автоматически регулируемыми насосами (см. главы 1 и 3). Общая схема такой автоматической системы регулирования дана на рис. 5.16, а. Насос 1 снабжен автоматическим регулятором 2, газогидравлическим аккумулятором 3 и предохранительным клапаном 4. Насос всасывает жидкость из бака 5. Устройства, относящиеся к элек - трогидравлическому приводу, обведены на схеме штриховым
|
Рис. 5.16. Система (а) с автоматически регулируемым источником энергопитания следящего электроги- дравлического привода и характеристика (б) насоса |
Контуром 6. В источник энергопитания входят также фильтр для очистки жидкости, датчики для контроля за уровнем и температурой рабочей жидкости в баке и другие вспомогательные устройства, не показанные на схеме, поскольку они не рассматриваются при составлении математической модели источника энергопитания. Характеристика регулируемого насоса показана на рис. 5.16, б.
Предположим, что чувствительный элемент регулятора (мембрана или поршень) является малоинерционным, поэтому приложенная к нему сила давления в любой момент времени уравновешена силой пружины. Изменение выходной величины (перемещение поршня или мембраны) условимся считать отрицательным, если оно вызвано увеличением регулируемого давления. При указанных условиях уравнение чувствительного элемента, записанное в малых отклонениях входной и выходной величин от своих установившихся значений, можно представить в виде
Л'р = - КкрР'п, (5.153)
Где Лр — отклонение выходной величины чувствительного элемента регулятора; р'п — отклонение регулируемого давления (входной величины) от заданного значения; К^р — коэффициент преобразования сигналов в чувствительном элементе.
Уравнение для исполнительного элемента регулятора, которым часто служит гидроцилиндр с одной рабочей камерой, не учитывая сжимаемость жидкости в этой камере, запишем в виде
|
|
Где Тс и Сс — постоянная времени и коэффициент относительного демпфирования исполнительного элемента (серводвигателя) регулятора; у'с — выходная величина исполнительного элемента (серводвигателя) регулятора; х'р — выходная величина усилителя регулятора (золотникового устройства); Кух — коэффициент преобразования сигналов усилителя в выходную величину исполнительного элемента.
|
(5.155) |
![]() Для обеспечения устойчивости рассматриваемой системы автоматического регулирования и возможности изменения ее статической характеристики (рис. 5.16,6) обычно применяют обратную связь от исполнительного элемента к усилителю. Одной из самых простых обратных связей может быть так называемая “жесткая обратная связь”, с учетом которой имеем
Для обеспечения устойчивости рассматриваемой системы автоматического регулирования и возможности изменения ее статической характеристики (рис. 5.16,6) обычно применяют обратную связь от исполнительного элемента к усилителю. Одной из самых простых обратных связей может быть так называемая “жесткая обратная связь”, с учетом которой имеем
Жр — — ^о. сУс?
Где К0,с — коэффициент обратной связи.
В малых отклонениях изменение подачи $н регулируемого насоса пропорционально у*с, поэтому
(5.156)
Где Кду — коэффициент преобразования перемещения исполнительного элемента, соединенного с регулирующим органом (например, шайбой аксиально-плунжерного насоса), в подачу насоса.
Уравнение расходов в напорном трубопроводе (гидролинии) насоса при описании происходящих в нем гидродинамических процессов в сосредоточенных параметрах составим с учетом газогидравлического аккумулятора, часто применяемого в источниках энергопитания в целях улучшения стабилизации давления. Уравнение представим в виде
|
|
Где ф;а — отклонение расхода жидкости, поступающей в газогидравлический аккумулятор; Уп, Вж и р„ — объем напорного трубопровода, модуль объемной упругости жидкости и отклонение давления в напорном трубопроводе; ф'гп — отклонение расхода жидкости, поступающей в гидропривод или в несколько гидроприводов, если все они подключены к общему источнику энергопитания.
При малых изменениях давления величина фа определяется линеаризованным уравнением:
Где Уа и ра — объем и давление газа в газогидравлическом аккумуляторе при заданном значении давления в напорной гидролинии; к = ср/су.
Уравнения (5.153) - (5.158) описывают динамическое состояние источника энергопитания с автоматически регулируемым насосом, частота вращения вала которого постоянна. Если во время процесса регулирования частота вращения вала изменяется, то к полученным уравнениям необходимо добавить уравнение движения вала двигателя насоса.
При расчетах динамических характеристик рассмотренной системы автоматического регулирования входное воздействие может быть задано как функция времени в предположении, что гидропривод заменен устройством (клапаном), которое создает требуемое изменение расхода фгП- Если необходимо исследовать динамику всей системы, состоящей из автоматически регулируемого источника энергопитания и одного или нескольких гидроприводов, то к уравнениям (5.153) — (5.158) необходимо добавить уравнения, описывающие процессы в гидроприводах. В этом случае входные воздействия на систему могут быть приложены в различных местах в зависимости от выбранных для исследования режимов работы системы.
При использовании в насосе регулятора прямого действия его математическая модель может быть получена из уравнений (5.153) - (5.154). Достаточно из указанных уравнений оставить только последнее, заменив в нем у*с на Лр и подставив в правую часть х^ = — К^р^. Соответственно потребуется изменить значения постоянной времени и коэффициента относительного демпфирования, которые теперь будут характеризовать динамические свойства регулятора прямого действия, непосредственно связанного с регулирующим органом насоса (с шайбой). В результате перечисленных операций уравнение регулятора прямого действия принимает вид
9 d2/i'n dh' , .
Tl + 2Cptp - Щ- + hv = -*ЛрРп, (5-159)
Где Тр, Ср и Kfy — постоянная времени, коэффициент относительного демпфирования и коэффициент преобразования сигналов регулятора прямого действия.
Уравнение (5.156) также следует записать с учетом того, что регулятор прямого действия не имеет исполнительного элемента, поэтому
Q* = KQhh'v, (5.160)
Где Кдь — коэффициент преобразования перемещения выходного звена регулятора прямого действия в подачу насоса.
Уравнения (5.157) и (5.158), очевидно, не требуются корректировать, так как они относятся к той части системы, которая не изменяется при использовании регулятора прямого действия. Необходимость в другой математической модели этой части может возникнуть независимо от типа регулятора, если вследствие большой длины гидролиний происходящие в них нестационарные процессы должны рассматриваться в распределенных по пространственным координатам параметрах.