Механика гидро - и пневмоприводов
Гидравлические модели течений рабочих сред
В общем виде движения рабочих сред подчинены рассмотренным выше фундаментальным законам механики жидкости и газа. Однако непосредственно применяя выражающие эти законы уравнения в технических расчетах, далеко не всегда можно получить необходимые для практики результаты. Такое положение объясняется тем, что для решения уравнений необходимо сформулировать граничные условия, описывающие взаимодействие рабочих сред с помещенными в них или их ограждающими телами. Граничные условия могут быть
Причиной гидродинамической неустойчивости движения среды, вследствие которой ламинарное течение переходит в турбулентное. Сложность процессов, происходящих в турбулентных потоках, не позволяет в полной мере воспользоваться общими уравнениями гидродинамики несмотря на то, что они остаются справедливыми. В связи с этим для учета диссипации механической энергии в турбулентных потоках обычно используют экспериментальные данные. Кроме того, при снижении давления до значений, близких к давлению насыщенных паров, в потоке жидкости возникает кавитация, вследствие которой нарушается условие неразрывности течения. Сложные процессы сопровождают течения газов со скоростями, превышающими скорость звука. Перечисленные и другие явления создают значительные трудности при математическом моделировании течений рабочих сред в реальных устройствах.
Эти трудности можно преодолеть, как развивая на основе общих уравнений механики жидкости и газа численные методы моделирования процессов в устройствах гидро - и пневмоприводов, так и достаточно широко применяя издавна известные методы гидравлических расчетов. При таких расчетах рассматривают уравнения и соотношения, записанные в усредненных по пространственным координатам скоростях, давлениях и температурах рабочих сред. Реальную структуру течений в гидравлических моделях отражают посредством коэффициентов, связывающих характеристики потоков с усредненными величинами и характеристики действительных потоков. Коэффициенты находят в результате решения предварительно упрощенных фундаментальных уравнений, обобщения экспериментальных данных и полуэмпирическим путем, используя совместно результаты расчетов и экспериментов.
В гидравлических моделях при выборе границ потока выделяют живые сечения, к которым ортогональны местные скорости, и вводят параметр, называемый гидравлическим радиусом
Где 5 — площадь живого сечения; X — смоченный средой периметр канала.
При напорном движении среды в круглой цилиндрической трубе гидравлический радиус равен половине радиуса проходного сечения трубы. Усредненную по живому сечению скорость V течения находят по соотношению
V = I и, (2.42)
5
Где и — местная скорость среды.
![]() Чтобы величины, вычисленные по скорости г;, совпадали с величинами, полученными для реального распределения местных скоростей в живом сечении потока, вводят коэффициенты кинетической энергии (коэффициент Кориолиса) а и коэффициент количества движения (коэффициент Буссинеска) /3. Коэффициент а равен отношению кинетической энергии среды, протекающей через данное живое сечение, к кинетической энергии, рассчитанной по усредненному значению скорости у:
Чтобы величины, вычисленные по скорости г;, совпадали с величинами, полученными для реального распределения местных скоростей в живом сечении потока, вводят коэффициенты кинетической энергии (коэффициент Кориолиса) а и коэффициент количества движения (коэффициент Буссинеска) /3. Коэффициент а равен отношению кинетической энергии среды, протекающей через данное живое сечение, к кинетической энергии, рассчитанной по усредненному значению скорости у:
|
5 |
Коэффициент /3 равен отношению количества движения среды с реальным распределением местных скоростей в живом сечении потока к количеству движения среды с усредненной скоростью у:
0=1^^ <2-44)
5
С помощью соотношения
И = (1 + 6щ) V формулы (2.43) и (2.44) можно представить в виде
А = 11(I + Зёи + Зё2и + ё3и) <1Б, (2.45)
5
0 = | У (1 + 2би + «2) <*5. (2.46)
5
Учитывая, что
|У^„<*5 = 0, (2.47)
5
По формуле (2.46) находим
| У 62и <1Б = 0 - 1. (2.48)
5
Используя формулы (2.47) и (2.48), выразим зависимость
(2.45) следующим образом:
А = 1 +3(0-1)(2.49) 5
Если ограничить возможные значения 6и пределами от —1 до +1, то по формуле (2.49) получим следующую приближенную зависимость коэффициента кинетической энергии от коэффициента количества движения:
А = 3(3-2. (2.50)
Например, при ламинарном установившемся течении ньютоновской жидкости в круглой цилиндрической трубе распреде
Ление местных скоростей по живому сечению потока описывает уравнение
И — ^шах^1 “ (2.51)
Где г*тах — местная скорость среды на оси трубы; г — координата, измеренная по радиусу сечения трубы до точки, в которой местная скорость и.
При этом течении по формулам (2.43) и (2.44) а 2, (3 1,33, а по формуле (2.50) а = 1,99, т. е. ошибка при
Ближенного вычисления не превышает 0,5%. В случае турбулентного течения в трубе а = 1,05... 1,12, /3 = 1,04. Из-за влияния различных устройств, расположенных перед входом в трубу, неравномерность распределения скоростей может возрасти, что приведет к увеличению значений а и /3.
|
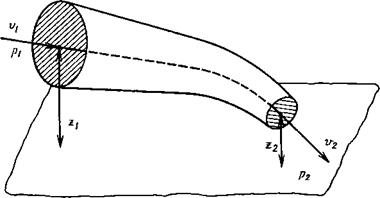
Рис. 2.9. Контрольные сечения канала при описании движения рабочей среды |
Рассмотренное без учета сжимаемости среды условие баланса мощностей потока в двух сечениях канала (рис. 2.9) позволяет записать уравнение
Гу , , «1 ръ гу, , «2^2 ,
Р9% 1 + Р1 Н 2— ~ М 2 + Р2 Н--------------- 2------ ^
I
(252)
О
Где (^ = = 52^2 — объемный расход среды, протекающей
В канале.
В уравнении (2.52) индексами “1” и “2” отмечены величины, взятые соответственно для сечений 1 и 2. Величина рс определяет потери давления вследствие гидравлического сопротивления канала. Последний член этого уравнения учитывает изменение давления, вызванное инерцией среды при неустановившемся течении. Уравнение вида (2.52) часто называют уравнением Бернулли для неустановившегося потока вязкой несжимаемой среды. Однако такое название не соответствует строгому выводу уравнения Бернулли, которое является по сути первым интегралом уравнения Эйлера, описывающего установившееся движение невязкой среды.
Уравнение (2.52) содержит коэффициенты «ь а2 и /?, которые обычно находят по экспериментальным данным, полученным при установившихся течениях. Для таких же течений определяют коэффициент гидравлического сопротивления, используемый при вычислении потери давления по формуле
2
Где С, — коэффициент гидравлического сопротивления, отнесенный к сечению канала, в котором усредненное по сечению канала значение скорости среды равно г;,*.
Коэффициент £,• зависит от формы канала и числа Рейнольдса, вычисляемого по соотношению
11е = (2.54)
Где Д, — гидравлический радиус или другой размер, характеризующий данный канал.
В случае установившегося движения среды последний
Член уравнения (2.52) обращается в нуль. Сложнее будет ситу
Ация, когда движение среды является неу становившимся. При гидравлических расчетах обычно принимают квазистационар - ные значения коэффициентов, получая их для установившихся течений среды с разными скоростями. Такой подход основан на замене реального нестационарного потока среды сменяющимися во времени потоками с установившимися распределениями местных скоростей по живому сечению. Выполненные с использованием квазистационарных значений коэффициентов расчеты неустановившихся процессов в ряде случаев с достаточной для практики точностью подтверждаются результатами экспериментов. Однако, согласно теоретическим и экспериментальным исследованям, распределения местных скоростей могут существенно изменяться в нестационарных потоках. Вызванные этими изменениями расхождения в нестационарной и квазистационарной моделях течения нетрудно заметить, рассматривая неустановившееся движение вязкой несжимаемой среды в круглой цилиндрической трубе длиной I. Для горизонтально расположенной трубы уравнение (2.52) принимает вид
Л1 dv рЬ (1в, ^ .
Р1 + ~2^ Ц + Рс = Р1 ~ Р2' ^ ^
По уравнению (2.11), пренебрегая массовыми силами, для той же трубы в проекциях на ее ось получаем
I
— J рих дУ = J PldS - J p2dS - J 27гготон (2.56)
V 50 50 О
Где тон — касательное напряжение на стенке трубы в нестационарном потоке среды; 5о = — площадь проходного сечения
Трубы.
Вычислив интегралы в уравнении (2.56) с учетом того, что, давления в пределах одного сечения имеют одинаковые значения, находим
Р1 ^ = (Р1 - Р2) 5о - 2ТГГ0/Т0Н, (2.57)
Где <2о = Зоу — объемный расход среды, протекающей в трубе.
После деления на 5о уравнение (2.57) принимает вид
А» 21т0н ( ,
Р1~П+------ — Р — Р2- (2.58)
Аъ г о
При установившемся течении из уравнений (2.55) и (2.58) следует, что
Рс = (2.59)
ГО
Где тоу — касательное напряжение на стенке трубы в установившемся потоке среды.
Если движение среды будет неустановившимся, то, как показывает сравнение уравнений (2.55) и (2.58), соотношение (2.59) можно применять только при /3 = 1,0. Однако это условие не соблюдается; в частности, при ламинарном потоке с ква - зистационарным распределением местных скоростей по живому сечению (3 = 1,33. Расчеты и результаты измерений местных скоростей также подтверждают существенное отличие нестационарного распределения скоростей от квазистационарно - го. Вследствие этого нестационарные касательные напряжения тон в принципе не должны совпадать с квазистационарны - ми значениями тоу.
Наряду с трубами, шлангами и другими каналами, длина которых значительно больше размеров, определяющих их проходные сечения, в гидро - и пневмоприводах широко применяют устройства с короткими каналами. Такие проточные элементы имеют постоянные или изменяемые во времени проходные сечения. Характеристики различных проточных элементов при установившихся течениях жидкостей и газов достаточно подробно изучены. Более ограничены сведения о влиянии на эти характеристики неустановившихся течений рабочих сред, что объясняется сложностью нестационарных гидродинамических процессов, которые могут в значительной мере зависеть от вида возмущений и предыстории самого процесса. При отмеченной неопределенности закономерностей неустановившихся течений необходимо определять границы, в пределах которых допустимо в расчетах использовать характеристики, полученные в случае установившихся течений. При колебаниях среды в коротком канале поток можно считать квазистаци - онарным, если
БЬ < 0,1(1 + 0,
Где С — коэффициент гидравлического сопротивления короткого канала; БЬ — число Струхаля:
Здесь ид — угловая частота колебаний потока среды; Д — гидравлический радиус отверстия; уу — установившаяся скорость истечения среды из отверстия.
Коэффициент гидравлического сопротивления короткого канала при установившемся течении зависит от числа Рейнольдса, поэтому указанное выше условие является косвенной оценкой совместного влияния вязкости и инерции среды на процесс истечения из короткого канала. Подобные оценки позволяют приближенно определить границы применимости ква- зистационарных коэффициентов гидравлических сопротивлений в расчетах динамических характеристик регулирующих и управляющих устройств приводов. Большое количество экспериментальных и теоретических характеристик различных аппаратов, рассчитанных с помощью квазистационарных коэффициентов, обычно подтверждают их хорошее соответствие друг другу.
Обобщая различные случаи механики нестационарных потоков рабочих сред, можно предложить следующий подход к использованию гидравлических моделей при расчетах и исследованиях устройств гидро - и пневмоприводов. Динамические характеристики устройств, имеющих короткие каналы с местными гидравлическими сопротивлениями, определяются при квазистационарных коэффициентах истечения. Волновые процессы в трубопроводах, шлангах и других длинных гидро - и пневмолиниях во избежание ошибок при расчете максимальных изменений давлений целесообразно рассматривать с учетом нестационарности коэффициентов сопротивления трения. Предлагаемый подход применен в дальнейшем при изложении вопросов математического моделирования и динамики гидро - и пневмоприводов.