ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ЧАСТОТНО­ЗАВИСИМЫМИ ЦЕПЯМИ

Частотно-зависимые четырехполюсники

В рассматриваемых ИП в качестве ЧЗЦ применяются, как прави­ло, ЧЗЧ.

На рис. 2.1 приведена классификационная схема ЧЗЧ, на которой представлены их основные типы. Пассивные ЧЗЧ, работающие в режи­ме холостого хода, характеризуются комплексным коэффициентом пе­редачи по напряжению. Выходной величиной пассивных ЧЗЧ, работаю­щих в режиме короткого замыкания, является ток короткого замыкания выхода; такие ЧЗЧ характеризуются комплексным проходным сопро­тивлением, определяемым как отношение их входного напряжения к выходному току.

Рис. 2.1. Классификация частотно-зависимых четырехполюсников

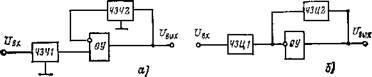
Активный ЧЗЧ представляет собой операционный усилитель ОУ, во входную цепь и цепь обратной связи которого включены пассивные ЧЗЦ, выполненные либо в виде четырехполюсников ЧЗЧ1 и ЧЗЧ2, работающих в режиме холостого хода (рис. 2.2,а), либо в виде цепей ЧЗЦ1 и ЧЗЦ2 типа частотно-зависимого сопротивления (рис. 2.2,6), представляющих собой двухполюсники или ЧЗЧ, работающие в режиме короткого замыкания. Характеристики активных ЧЗЧ, схема которых показана на рис. 2.2,а, при синусоидальном и импульсном сигналах определяются соответственно равенствами

К«ю)=К,(/©)/*,(/») и К(Є)-Л(Є)/^»(Є), (2.1)

где /= V=i ;Ki(/со) и К2(/со) —комплексные коэффициенты передачи четырехполюсников ЧЗЧ1 и ЧЗЧ2 Fi(0) и /^(0)—характеристики
тех же четырехполюсников, реализованных в виде ПДА. В ИП пре­имущественно используются амплитудно-частотные характеристики ЧЗЧ, при рассмотрении которых первое из равенств (2.1) заменяется выражением

/((co) = |/(i(/co)//(2(;co)|. (2.2)

Амплитудно-частотная характеристика активных ЧЗЧ, схема кото­рых представлена на рис. 2.2,6, работающих только при синусоидаль­ном сигнале, определяется равенством

/((co)=-|Z2(/co)/Z1(/co)|, (2.3)

где Zi(/co) и Z>2 (/со)—комплексные проходные сопротивления целей ЧЗЦ1 и ЧЗЦ2.

Как следует из (2.1) — (2.3), функция преобразования ИП с актив­ными ЧЗЧ определяется характеристиками двух пассивных ЧЗЦ. Вза­имный Подбор этих характеристик позволяет значительно расширить класс функций преобразования, реализуемых с малыми методическим» погрешностями или без них (по сравнению с ИП, содержащими только одну пассивную ЧЗЦ).

Многозвенные ЧЗЧ (рис. 2.3) представляют собой каскадное со­единение через развязывающие усилители РУ1—РУп—1 однозвенных пассивных или активных ЧЗЧ (ЧЗЧ1—ЧЗЧ п). Они имеют один вход и п независимых выходов, каждый из которых при идентичности ха­рактеристик F(со) или F(0) каскадно соединенных ЧЗЧ может быть использован для получения степенной зависимости вида [F(co)]* илв [F(0)]‘ (*=1, 2, ... я).

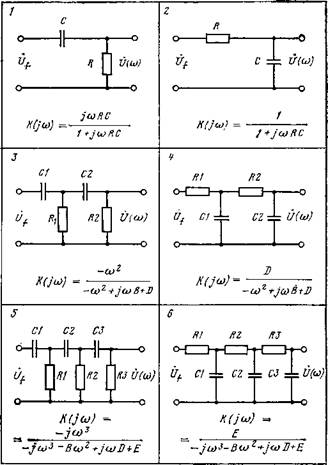
В табл. 2.1 приведены схемы пассивных ЧЗЧ, работающих в ре­жиме холостого хода [14]. Они позволяют получить при синусоидаль­ном сигнале функции преобразования в виде степенных функций у = =хк (&= + 1, +2, ±3). Как следует из приведенных в табл. 2.1 вы­ражений для комплексных коэффициентов передачи ЧЗЧ, схемы /, 3 и 5 позволяют приближенно получить соответственно пропорциональ­ную, квадратичную и кубическую зависимости при выполнении усло­вий, обеспечивающих приближенное равенство знаменателей выражений для /С(/со) постоянной, не зависящей от частоты, величине в заданном, рабочем диапазоне частот. Например, при помощи схемы 1 (диффе­ренцирующей цепи) можно аппроксимировать пропорциональную зави­симость | /С (/со) | =о/?С, если в заданном диапазоне частот выполняет­ся неравенство о>2/?2С2<1. Однако при выполнении подобных условий ИП будут иметь методические погрешности, определяе­мые отличиями указанных знаменателей от единицы, величин D и Е (в табл. 2.1 £, D и Е — постоянные, зависящие от параметров схем) для схем 1, 3 и 5 соответственно. Если в схему активных ЧЗЧ (см. рис. 2.2,а) включить во входные цепи и цепи обратной связи ОУ пары схем 1 и 2, 3 и 4, 5 и 6, то согласно (2.2) знаменатели выражений для коэффициента передачи /С(усо) данных схем сокращаются и получают­ся без методических погрешностей зависимости соответственно /С(со) = =©/?С, /C(co)=co2/D и /С(со)=со3/£.

Если рассматриваемые пары схем пассивных ЧЗЧ поменять места­ми в схеме активного ЧЗЧ, то, как следует из (2.2), реализуются без методических погрешностей зависимости К(CD)s=CD-i (i=l, 2, 3).

Схемы 3—6 являются многозвенными. Однако ввиду отсутствия развязывающих каскадов между /?С-ячейками они не обладают отме­ченным выше свойством многозвенных ЧЗЧ.

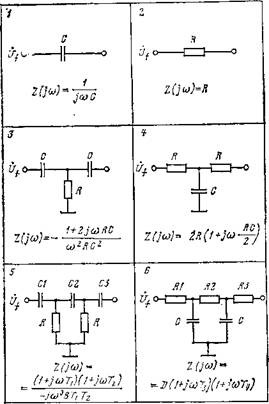
В табл. 2.2 приведены схемы пассивных ЧЗЦ типа частотно-зави­симого сопротивления [14], которые обеспечивают те же возможности по воспроизведению степенных функций, что и схемы, обозначенные в табл. 2.1 теми же номерами. Согласно (2.3) и выражениям для ком­плексного сопротивления Z(jсо), приведенным в табл. 2.2, для получе­ния квадратичной и кубической зависимостей при помощи активных ЧЗЧ (см. рис. 2.2,6) числители выражений для Z(/(о) схем 3 и 5 с точ­ностью до постоянных коэффициентов должны совпадать с выражения­ми для Z(/(о) схем 4 и 6 соответственно. Однако, как видно из табл. 2.2, для этого требуется определенный подбор значений парамет­ров элементов схем (в схемах 5 и 6 постоянные времени 7^—Т4 определяются существенно различными зависимостями от параметров схем). Связанные с этим подбором дополнительные трудности расчета и настройки активных ЧЗЧ на рис. 2.2,6 определяют их недостаток по сравнению с активными ЧЗЧ на рис. 2.2,а.

Использование вещественных и мнимых частей амплитудно-фазо­вых характеристик ЧЗЧ позволяет расширить класс функций преобра­зования, реализуемых при помощи ИП с ЧЗЧ. Например, в качестве пассивного ЧЗЧ, работающего в режиме холостого хода, может быть применена линия задержки, имеющая комплексный коэффициент пере­дачи /С(/(о) =e-j«T? Где т — время задержки. Использование частотных характеристик

Re (е—/ют) —cos ют; 1т (е—/ШТ) =—sin or (2.4)

дает возможность построить ИП с функциями преобразования в виде тригонометрических функций [6].

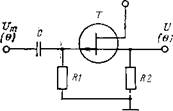
Как отмечено выше (см. § 1.1), ЧЗЧ, работающие при импульс­ном сигнале, реализуются в виде ПДА. Принципиальная электрическая схема простейшего ПДА, состоящего из последовательно соединенных фильтра верхних частот и однополупериодного выпрямителя, показана на рис. 2.4. Цепочка R{C является фильтром верхних частот, а исто -

ковый повторитель на полевом транзисторе Т, не пропускающий отри­цательную часть поступающих на него импульсов, выполняет функцию однополупериодного выпрямителя. Одновременно этот же истоковый повторитель в ряде случаев служит развязывающим усилителем. Та­кой ПДА имеет линейную характеристику F(0) = 1—0 = 0, где 0 —

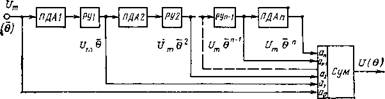
инверсия сигнала 0 (относительная длительность паузы). Поэтому реа­лизация функций различных степеней путем соединения однозвенных ЧЗЧ в многозвенные наиболее целесообразна на основе ПДА. На рис. 2.5 приведена схема многозвенного ПДА, состоящего из каскадно соединенных простейших ПДА (ПДА1—ПДАп) и сумматора Сум [15]. Напряжение на k-м выходе многозвенного ПДА

U*=Uk-fi=Unfik,

где Um — амплитуда входного импульсного напряжения. Рассматри­ваемый ПДА имеет характеристику вида степенного полинома

F (а) = 2 а#к< (2-6>

k=0

где ak — весовые коэффициенты суммирования; п — число каскадно со­единенных простейших ПДА. Знаки и значения коэффициентов а* уста­навливаются в соответствующих входных цепях Сум. Наличие в функ­ции F(0) постоянной (т. е. не зависящей по амплитуде от значения 0) импульсной составляющей, для которой & = 0, обеспечивается соедине­нием одного из входов Сум с входом ПДА.

Рис. 2.4. Принципиальная

электрическая схема простей­шего ПДА

С помощью данного ПДА можно воспроизвести различные транс­цендентные зависимости /’’(б) путем их полиномиальной аппроксима­ции в соответствии с (2.6).

При включении подобных ПДА в активный ЧЗЧ (см. рис. 2.2,а) можно использовать дробно-рациональную аппроксимацию требуемых зависимостей согласно второму равенству (2.1), обеспечивающую наи­большие возможности получения малых методических погрешностей при воспроизведении многих функций [16].