Гранулирование

Определение максимальной скорости уплотнения

Процесс фильтрации воздуха через слой порошка при не­прерывном уплотнении сопровождается рядом сложных явле­ний, физическая сущность которых до настоящего времени недо­статочно ясна. Очевидно, что критическая скорость фильтрации воздуха через слой порошка в процессе его непрерывного уплот­нения должна определять максимально допустимую скорость его уплотнения.

Различными авторами предложены модели вытеснения газо­вой фазы из порошков. На основании их анализа получены за­висимости для определения максимально допустимой скорости прессования (прокатки). Так, предложено [64] уравнение для расчета максимальной скорости прокатки порошкообразных ма­териалов, полученное на основе исследования аэродинамики зернистых материалов в аппарате цилиндрического типа:

^в. кр= (£/2р, аг) (ДР/Л,)Кр, (3.12)

где k — коэффициент проницаемости порошка; |хг— вязкость газа; а — угол захвата; (Ар/!ц)кр — давление, соответствующее появлению первых при­знаков повышения уровня порошка при фильтрации воздуха через слой в цилиндрическом стакане высотой hi.

При выводе зависимости (3.12) предполагалось, что выдав­ливаемый из порошка воздух движетсд равномерно, в основном в направлении, обратном прокатке. Использование зависимости

(3.12) для практических целей в настоящее время затруднено по следующим причинам:

в каждом конкретном случае оно предполагает эксперимен­тальное определение эмпирических констант (k и АР);

не учитывает влияния параметров уплотнения порошкооб­разных материалов и конструктивных размеров валковых прес­сов.

Следует также отметить, что формула (3.12) получена на основании исследования аэродинамики порошков в аппарате цилиндрического типа. Фильтрация же газовой фазы при уплотнении порошков на валковых прессах происходит в кана­ле переменного по высоте сечения.

В дальнейших исследованиях аэродинамики порошков в процессе их непрерывного уплотнения было сделано предполо­жение о том, что основная часть заключенного между частица­ми газа вытесняется из порошка. Если скорость вытеснения га­за превышает определенные значения, то порошок в зоне пода­чи переходит в псевдоожиженное состояние. Используя пред­ставления о псевдоожижении, с учетом формы зоны деформа­ции и подачи порошка, автор сравнивает скорость вытеснения газовой фазы из порошка и скорость начала псевдоожижения. При этом используется обобщенное уравнение М. Лева для оп­ределения скорости начала псевдоожижения:

Gm=0,00923d'-8S [рг(р„ — рг)1 °.9</Цг°'88 (3.13)

(где Gm — расход газа при минимальном псевдоожижении).

Скорость вытеснения газа из порошка при непрерывном уплотнении имеет вид [64]:

G= (2jtRB2zjBpr/p) {(a — sin ап cos а„)/[2Рв(1 — cos ап)+Л]ап}.

(3.14)

Проведенное сопоставление расчетных и экспериментальных значений верхних критических скоростей для медного порошка показало, что реальная верхняя критическая скорость при на­чале псевдоожижения в 10 раз выше, чем расчетная [64]. В дальнейшем сравнивались скорость псевдоожижения порош­ков в модели прокатного стана с диаметром валков 0,512 м и критическая скорость прокатки по формуле (3.14). При этом экспериментальная максимальная скорость прокатки для алю­миниевого порошка составила 35,8 м/мин, а начало псевдоожи-

жения этого порошка наблюдали при скорости воздуха, соот­ветствующей прокатке 4,8 м/мин.

Расчет верхней критической скорости прокатки порошков [65] основан на том, что не весь газ, выдавливаемый из по­рошка, движется в направлении, обратном прокатке. Используя гипотезу плоских сечений, авторы предположили, что мгновен­ное сжатие объемов порошка в зоне прессования приводит к повышению давления газа в порах. При этом зависимость из­быточного давления газа от угла поворота валка AP=f'(a) аналогична зависимости изменения объема AV/V=f(a). Избы­точное давление газа в зоне прессования обусловливает его фильтрацию в направлении наименьшего сопротивления. Вы­разив фильтрующую способность порошка в сечении, соответст­вующем углу подачи, через уравнение Дарси, а объем газа, выдавливаемого из этой зоны на длине дуги, равной приблизи­тельно одному градусу, через параметры процесса прокатки, авторы [65] предлагают выражение для расчета верхней кри­тической скорости вращения валков:

IV кр « М Я/ 0,08рга < 12,5 kAP/pra. (3.15)

Избыточное давление АР, при котором происходит нару­шение сплошности порошка, авторы предлагают оценивать че­рез такие характеристики, как коэффициент внутреннего тре­ния порошка, его насыпную плотность и некоторые геометриче­ские размеры бункерного устройства. Приняв для порошка ги­потезу о сплошности, можно, отмечается авторами, написать уравнение условия предельного равновесия сыпучего тела в точ­ке (или на элементарной площадке) в форме напряжений:

(ДР) кр= о tg q>+c', (3.16)

где с' — некоторая постоянная величина, характеризующая сцепление по­рошка.

Тогда с учетом (3.16) уравнение (3.15) принимает следую­щий вид:

iVkp<£ (о tg <p+c')/0,08p, rfl. < (3.17)

Выражая величину нормального напряжения при прокатке порошков как сумму давления порошка в зоне подачи, давле­ния, создаваемого бункерным устройством, и величины избы­точного нормального напряжения, авторы получили уравнение для расчета верхней критической скорости при прокатке с бун­керным устройством, которое приводится в работе [65], и без бункерного устройства:

і'іі. крСбр. іЯ B(sin а — sin an)tg <р/0,08ргв. (3.18)

На основании проведенного анализа работ, посвященных изучению модели вытеснения воздуха из порошков в процессе их уплотнения на вальцевых уплотнителях, можно сделать не­сколько замечаний.

В работах [64, 65] не вполне обоснованным является ис­пользование гипотезы плоских сечений для определения аэро­динамических характеристик слоя порошка в зоне уплотнения валкового пресса (прокатного стана). По утверждению автора, лишь 8% выдавливаемого из порошка газа фильтруется через слой в направлении, обратном прокатке. Это утверждение по­служило основой при выводе уравнений (3.15), (3.18).

При выводе уравнения (3.15) автором для определения пе­репада давления слоя порошка в зоне уплотнения использова­на формула, предложенная в работе М. Лева и справедливая лишь для аппаратов цилиндрической формы. Непрерывное уплотнение порошкообразных материалов на валковых прессах (прокатных станах) сопровождается, как указывалось выше, фильтрацией газовой фазы в канале, образованном двумя ци­линдрическими поверхностями. Следовательно, аэродинамичес­кие характеристики слоя порошкообразного материала в кана­ле указанного типа должны отличаться от характеристик слоя, находящегося в аппарате цилиндрического типа.

На основе предположения термодинамической общности фа­зовых превращений в псевдоожиженных системах и капельной жидкости, выдвинутого Н. Б. Кондуковым и М. X. Сосной, раз­работан [38] прогноз качественного развития фазовых превра­щений при фильтрации газа через слой зернистого материала в канале, образованном двумя цилиндрическими поверхностями.

Считая переход неподвижного слоя в псевдоожиженное со­стояние подобным плавлению твердого тела, а унос частиц из слоя аналогичным переходу жидкости в парообразное состоя­ние, авторы говорят о трех возможных агрегатных состояниях (фазах) системы твердые частицы — ожижающий агент: твер­дом (неподвижный слой), жидком (псевдоожиженный слой) и парообразном (унос). Следуя термодинамической сущности аналогии и применяя правило фаз к системе твердые части­цы— ожижающий агент, состоящей из N і компонентов и фі фаз, авторы получили следующее выражение для вариантности системы:

fi=Ni — фі - f - 1 •

Далее авторы отмечают, что если система монодисперсна (Л"i = l), то возможно существование одной фазы в некотором диапазоне скоростей ожижающего агента (fj = l, так как <pt = = 1), а также предполагают возможность существования двух фаз при какой-либо фиксированной скорости ожижающего аген­та (система нонвариантна): ft = 0, так как <pi=2.

На основании изложенного, сделано предположение [38], что при скорости прессования порошков, превышающей допус­тимые пределы, возможно существование двух фаз в канале, образованном двумя цилиндрическими валками. То есть мате­риал, находящийся в зоне уплотнения, при определенной скоро­сти вращения валков (превышающей допустимую) будет нахо­диться в состоянии, близком к псевдоожиженному.

Таким образом, максимальную скорость прокатки порошко­образных материалов следует определять по критической ско­рости фильтрации газа через слой, находящийся между валка­ми, без нарушения его плотности.

Критическая скорость псевдоожижения мелкозернистого ма­териала в канале, образованном двумя цилиндрическими по­верхностями и стенами бункерного устройства, может быть оп­ределена по методике, изложенной в работе [38]. Но при этом необходимо сделать допущение, что профиль такого канала аналогичен профилю коническо-цилиндрического аппарата. При больших диаметрах валков (0,9—1,2 м) и малых зазорах меж­ду ними (2—7 мм) указанное допущение не внесет значитель­ной погрешности при определении критической скорости псев­доожижения.

Нарушение устойчивости слоя в аппаратах такого типа на­ступает [66] в момент, когда при увеличении скорости сила аэродинамического взаимодействия потока с частицами мелко­зернистого материала становится равной весу материала в ап­парате. Рассматривая стационарный процесс фильтрации не­сжимаемой жидкости и пренебрегая влиянием стенок аппарата на течение, авторы [66] получили математическую формули­ровку выдвинутого предположения в виде:

Г = — J grad *> =Ссл, (3.19)

V

—►

где Т — сила, действующая на слой со стороны фильтрующего потока; Сел — вес материала в слое.

Это выражение, как отмечают авторы, позволило им опре­делить критическую скорость Wo, отнесенную к входному сече­нию коническо-цилиндрического аппарата.

При решении указанной задачи авторы предположили, что в конической зоне аппарата (рис. 3.4) поле давления зависит только от радиуса г. Изобарные поверхности представляют со­бой части сфер, ограниченных боковой поверхностью конуса, а в цилиндрической зоне аппарата давление зависит только от

5—631

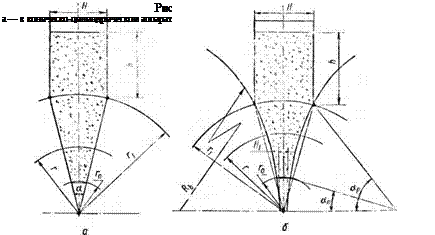высоты слоя, т. е. P — P(h). Принятая картина поля давления в коническо-цилиндрическом аппарате, как отмечают авторы [66], лишь приближенна. Однако целью исследования является определение критической скорости, значение которой опреде­ляется силовым взаимодействием потока с материалом в слое в момент псевдоожижения, а не выяснение точной структуры по­ля давлений. Поэтому принятая идеализация служит лишь вспомогательным средством.

По формуле Эргуна для конической зоны (с граничным условием при г=Г P=Pi):

dP= [AwoUP+B w04/r*] dr, (3.20)

где у4 = 150рг02(1 — ei)2v/ei3d2; £=1,75рг04(1 — ві)/еі3£? где Єї—порозиость слоя; v — кинематическая вязкость газа.

Для цилиндрической зоны:

dP= [(Лшо/г.2) + (Ви»ог/гі4)]Й2, (3.2!)

где z — текущее значение высоты слоя.

Граничным условием в этом случае служит равенство нулю давления на свободной поверхности слоя Pz=h=0. Общее реше­ние задачи для любого режима течения достаточно громоздко. Поэтому, как указывают авторы [66], целесообразно найти ре­шение для ламинарного и турбулентного режимов раздельно. Для ламинарного режима зависимость перепада давления при фильтрации газа через слой материала от скорости является линейной:

P=Aw0[(lfr)—(l/ri)-)-(h/r,2)]. (3.22)

Тогда сила для конической и цилиндрической частей аппара­та, действующая со стороны потока на материал, может быть выражена следующими уравнениями:

j* gradP (to = я sin2a/2 (rt — r0) AwB, (3.23)

rKOH

j* grad P do = J (dP/dz) dt> = nR2mnhX

гцил

X. Awolrl2=Aw0fmsin1 a/2. (3.24)

Таким образом, согласно (3.19):

T = J* gradPdu-f J grad P do = nAw0 sin2 a/2r0 (я - f N — 1), (3.25)

DKOH °цил

где n=r,/r0=Z)/d0; N=hlrB.

В результате определения поля давления в коническо-ци­линдрическом аппарате и выражения массы слоя как произве­дения объема на насыпную плотность материала (с учетом ар­химедовой силы) авторы [66], исходя из уравнения (3.19), по­лучили аналитические уравнения для определения критической скорости псевдоожижения, отнесенной к нижнему сечению ко­нуса: для ламинарного режима фильтрации слоя (Re^lO)

ReKp=Ar(n3+3Wn2 — 1)е, э/450(1 — е,) (л+А — 1), (3.26)

для турбулентного режима (iRe>10)

ReKP= [Аг(л3+ЗАл2 — 1)л2е,3/5.25(л2+А — л)]1'2. (3.27)

При отсутствии цилиндрической части выражения (3.26),

(3.27) переходят в соответствующие уравнения для конических камер:

при ламинарном режиме

ReKP=Ar(n3 — 1)е,*/450(1 — е,) (п - 1), (3.28)

при турбулентном режиме фильтрации

ReKP= [Аг (л3 — 1)л2е,3/5,25л(л — 1)] ‘/2. (3.29)

С учетом ранее принятых допущений уравнения (3.26),

(3.27) могут быть использованы для определения критической скорости фильтрации газа через слой порошка при его уплот­нении в валковых прессах с бункерным устройством, а уравне­ния (3.28), (3.29) при работе без бункеров-накопителей; при этом hi—H/Hi; Ni=2holHii Н — [/іл+2/?„(1—cosctn)].

Объем газа, выдавливаемого при непрерывном уплотнении (с учетом фильтрации по кромкам) может быть рассчитан по уравнению:

V=(z— l)ZVww, (3-30)

где z—степень уплотнения порошка, z=pn/pH; Lv—рабочая длина валка; 5* 67

hn — толщина ленты после валкового пресса; i»max— максимально допустимая скорость вращения валков.

В свою очередь, объем газа, выдавливаемого при непрерыв­ном уплотнении слоя материала, может быть определен, исхо­дя из критической скорости фильтрации газовой фазы:

V<wKpF<wKPLphv, (3.31)

V<ReKpLpfcj, v/d. (3.32)

Решая совместно уравнения (3.30), (3.32), получим:

iW<[ReKp/(z— 1)] (v/d). (3.33)

Подставляя значения ReKp из (3.26), (3.27), получим анали­тические уравнения для определения максимально допустимой скорости вращения валков.

При работе с бункером-накопителем: для ламинарного режима фильтрации газовой фазы (Re^lO)

гтах< [Аг(лі3+ЗЛГ, Ліг— l)ei3/450(l — е,) (n,-f-Wi — 1) (Z— l)]v/d.

(3.34)

для турбулентного режима (Re>10)

tWcdArOl. M-SWn,* — 1) n,2e,*/5,25 (n. a+JV, — n,)]‘/2/(z— l)}v/d;

(3.35)

При работе валковых прессов без бунке - р о в-н акопителей: для ламинарного режима (Res^lO)

^т. х<[Аг(л13— 1)еі3/450(1 — Єі)(лі— l)(z— 1)] (v/rf), (3.36)

для турбулентного режима (Re> 10)

tW<{[Ar(n,3- 1)в,*в,^5дая,(Я| — 1)] 1/a/(z— l)}v/d (3.37)

Анализ уравнений (3.34) — (3.37) позволил теоретически обосновать основные технические направления интенсификации процессов прессования:

при прокатке порошков следует производить вакуумирова­ние зоны деформации валкового пресса;

прокатку следует производить в газовой среде с кинемати­ческой вязкостью меньшей, чем у воздуха;

на прессование должна поступать шихта определенного дис­персного состава;

следует производить предварительное уплотнение порошко­видных материалов в бункере валкового пресса.

Поскольку реализация первых трех технических решений в условиях многотоннажного производства удобрений сопряжена с большими затратами энергоресурсов, наиболее эффективным путем интенсификации процесса прессования следует считать предварительное уплотнение порошков.