Гранулирование

Кинетика гранулообразования в аппаратах барабанного типа

Одна из первых попыток описать изменение размера гра­нул в зависимости от параметров процесса гранулирования ме­тодом окатывания предпринята Капуром и Фьюстером (цити­руется по работе (231). Авторы делят процесс гранулообразо­вания на три этапа. На начальной стадии процесса образуются ядра, размер которых не превышет 0,1—0,5 мм. На втором этапе (переходная стадия процесса) по мере образования ядер избыточная влага выдавливается на поверхность гранул. Влаж­ная оболочка ядра обеспечивает рост гранул за счет простого наслаивания или агломерации ряда частиц. На заключитель­ной стадии процесса происходит рост гранул и их дробление на более мелкие частицы. Рост гранул авторами оценивается уменьшением удельной поверхности гранул в виде следующего уравнения:

1п(Д — F0)—ku)+C, (2.1)

где F — удельная поверхность ядер на единицу объема; «а — частота враше - 34

пня барабана: к—константа скорости роста; Fa, С — постоянные, определяе­мые из экспериментальных данных.

Известны и другие работы, в которых рассматриваются раз­личные механизмы образования гранул в зависимости от раз - мера исходных частиц. Принимая, что движущейся силой про­цесса гранулирования является сила сцепления частиц в агло­мерате, авторы работы [39] предлагают следующую зависи­мость для расчета среднего размера гранул;

dcp—doexp m(Qx —Qo)n, (2.2)

где rfCp—средний диаметр гранул; d0 — диаметр гранул в начальный момент гранулообразования; Qx — содержание жидкой фазы; Q0 — содержание жид­кой фазы в момент начала гранулообразования; т, п — эмпирические коэф­фициенты, определяемые опытным путем.

Для веществ, нерастворимых в связующем, в работе [40] принимают, что движущая сила целиком определяется коли­чеством связующей жидкости, вводимой извне, т. е. влагосодер- жанием шихты. При этом Qx = u. Для растворимых веществ ве­личина QK зависит от коэффициента растворимости S:

<2ж=«(1 + S)/(l — uS). (2.3)

Поскольку на растворимость 5 влияет температура, то с увеличением последней растет величина Q>K. Чем выше темпе­ратура, тем меньше требуется вводить жидкой фазы извне, по­скольку она образуется внутри системы в результате повыше­ния растворимости.

Средний диаметр гранул зависит также от количества вво­димого сухого ретура gp и размера частиц ретура dp. Чем боль­ше ретура и чем он крупнее, тем меньше поверхность частиц и выше их влагосодержание.

Диаметр гранул может определяться по формуле [40];

dCP=do exp{m [С? ж/(1 — gp — gpdo/dp) — Q0] n} (2.4)

(где gp — относительное количество ретура в продукте). Фор­мула (2.4) справедлива лишь в случае, если ретур не поглоща­ет влагу.

Реально используемый при гранулировании удобрений ре­тур при смешении с влажным порошком с течением времени насыщается влагой. Содержание жидкой фазы на поверхности окатываемых частиц при этом уменьшается на то количество влаги, которое диффундировало внутрь гранул ретура, т. е. на величину iipgp (где Up — влагосодержание ретура). Влагосодер­жание ретура зависит от времени контакта, температуры и т. д. Поэтому авторы [40] приводят расчетную формулу для опреде­ления среднего диаметра гранул, полученных методом окаты­вания, к следующему виду:

dCp =dо exp{rafQ»/(l — gp — gpd0/dp) — Оо+КрЫ"}. (2.5)

Зависимость (2.5) может быть использована только при
<?обЩ= [<?ж/(1 — gp — gpdo/dp)] — Upgp>Q0,

когда влагосодсржание шихты превышает минимальное зна­чение, необходимое для гранулообразования. При Q06iu<Q>k гранулообразования не происходит.

В работе [41] процесс гранулирования в барабане рассмат­ривается как вероятностный, характеризующийся беспорядоч­ным движением, перемешиванием и агломерацией частиц в плотном слое. Авторы [41] разработали полуэмпирическую мо­дель, включающую один параметр — функцию плотности рас­пределения гранул. Отмечается, что сравнение модели с экспе­риментальными данными показало хорошую корреляцию в ши­рокой области варьирования параметра гранулируемой си­стемы.

Исследованиями процесса роста гранул влажного песка [42, 43] установлено, что максимальный размер частиц тем меньше, чем меньше поверхностное натяжение связывающей жидкости. Приведено [43] критериальное уравнение, описываю­щее распределение гранул по размерам. Предложена [44] мо­дель коалесценции двух контактирующих гранул, подвержен­ных осевой сжимающей и разъединяющей силам. Представле­на диаграмма напряжений в зоне контакта.

В работах [45—52] приводятся результаты теоретических и экспериментальных исследований процессов гранулирования, а также динамики движения материала.

Рассмотренные выше зависимости для расчета роста гра­нул и установленные закономерности гранулирования, как пра­вило, носят частный характер. Их применение ограничено усло­виями тех экспериментов, данные которых необходимо исполь­зовать в расчетных выражениях.

Предложен [21] излагаемый ниже аналитический метод расчета диаметра частиц при гранулировании с использовани­ем грануляторов барабанного типа. Авторы предположили, что при движении гранулы по спиралевидной траектории на протя­жении пути АI ее диаметр увеличивается на величину Ad, рав­ную 2NK:

N^AlJnd, (2.6)

где N — число оборотов гранулы вокруг своей оси на пути А/; Л—толщина наслаивающейся пленки.

С другой стороны А/ определяется как

Д/=(Л6юМ>с)Д£б, (2.7)

где Rc, — радиус барабана; <о — угловая частота вращения барабана; шос — скорость движения продукта вдоль оси барабана: Lc—длина барабана.

Обозначая в уравнении (2.7) AL^I'w через Ат, с учетом (2.6) после дифференцирования получим:

ddd= (2Rtti>ln)Mx. (2.8)

Уравнение (2.8) представляет собой математическую модель роста частиц при гранулировании методом окатывания.

В общем случае изменение гранулометрического состава во времени может быть описано уравнением

Р (d) d [р (d) ] = (2/?6со/л) р (Я) dx, (2.9)

где p(d)—плотность распределения частиц по размерам; р(Я)—плотность распределении пленок, наслаивающихся на пути АI.

На практике гранулометрическая характеристика материа­ла определяется ситовым анализом и представляется дискрет­ными фракциями. Тогда уравнение (2.9) для ї-го интервала можно записать так:

diddi=2R6u>fadxln, i= 1; 2, .... n. (2.10)

Рассмотрим частные случаи уравнения (2.10).

1. Пусть Я/=const, т. е. предполагается, что в течение всего времени гранулирования на гранулу і-го размера наслаивается на каждом участке А/ пленка одинаковой толщины Я*. Примером может служить процесс гранули­рования увлажненной шихты при назначительном количестве ретура, т. е. когда по всей длине гранулятора вероятность столкновения ядра с наслаи­вающимися частицами одинакова.

В результате интегрирования уравнения (2.10) при Я,-=const получим: dt = (d*ig +- 4%оЯгт/л)1/2, (2.11)

где di —начальный размер частицы і-й фракции.

2. Пусть в момент времени т=0 Я, = Яі0, т. е. в начальный период про­цесса гранулирования происходит наслаивание пленки толщиной Я;0, а при увеличении т Я,-—>-0, т. е. на гранулу наносится пленка все меньшей толщи­ны из-за уменьшения вероятности столкновения гранулы с наслаивающи­мися частицами и уменьшения количества жидкой фазы на поверхности ядра. Такой механизм процесса гранулирования наблюдается прн значитель­ном избытке ретура. В этом случае можно рассмотреть два варианта ре­шения уравнения (2.10).

Если толщина наслаиваемой на гранулу пленки уменьшается по длине барабана по линейному закону

Я; = Я,-о —kxx (2.12)

(где к — кинетический коэффициент в м/с, зависящий от свойств гранули­руемого материала и параметров процесса), то, подставляя (2.12) в (2.10), получим

di ddt = 2/?бы (Я,-0 — бут) dx/я. (2.13)

После интегрирования этого уравнения будем иметь:

dt «= [d2ip + 2Яб<й (2Я,-0 - /дт) х/л] 1/2. (2.14)

Если толщина наслаиваемой пленки уменьшается по экспоненциальному

закону

Яг = Я,0ехр(-*2Х) (2.15)

(где &2 — кинетический коэффициент в С”1), то, подставляя (2 15) в (2.10), получим:

d( ddt = 2/?б(оЯ(.0 exp (— kit) dx/ я. (2.16)

Проинтегрировав уравнение (2.16) для каждой 1-й фракции, получим: di = {d+ 4Я/рЯбсо [1 _ exp (—kit)]/nkzp. (2.17)

До сих пор рассматривались идеальные процессы роста гра­нул при условии неизменности их структуры, отсутствия истира ния, дробления и других сопутствующих процессов, приводящих к изменению размера гранул.

Реальные процессы гранулирования, протекающие в плот­ных гравитационных слоях дисперсной фазы, сопровождаются, как правило, уплотнением структуры формируемых гранул, их истиранием, измельчением и т. п.

Учитывая тот факт, что при гранулировании порошкообраз­ных материалов окатыванием наряду с процессами роста гра­нул протекают процессы, приводящие к уменьшению их разме­ров, под толщиной наслаиваемой пленки необходимо понимать разность:

Ь = Ч~Ч, (218>

где hir, Х;и — толщина наслаивающейся и истирающейся пленки за один оборот гранулы вокруг собственной оси і-й фракции.

С учетом (2.18) уравнение (2.10) можно записать в виде

diddi = 2 R<jW h, г-и) dr/л. (2.19)

В зависимости от технологических и гидродинамических па­раметров процесса гранулирования, можно выделить следую­щие частные решения уравнения (2.19).

При уравнение (2.19) имеет решения (2.11), (2.14),

(2.17).

При ‘kiK~>'kir, т. е. когда процессы истирания превалируют иад процес­сами роста гранул, уравнение (2.19) имеет три решения:

при ^ги = const dt = [d2i() — 41?бО&гит/л]1 /2; (2.20)

при hiu=Xio—k'iх di — [^г0 = 2%о(2Л, го~-*,1г) т/я]1/2; (2.21)

при Хік = Я,,-0ехр (— kx) di = {d2i0— 4Х(-0Ябы/л&'2[1 —

— exp(— k'2x)]}42t (2.22)

где k/, k2— кинематические коэффициенты истирания гранул, соответствен­но имеющие размерность м/с и с-1.

В общем случае, когда ^,и и far величины одного порядка, решения уравнения (2.19) принимают более сложный вид. Для различных условий гранулообразования решения уравнения (2.19) сведены в табл. 2.1. Пользуясь этими уравнениями, мож­но рассчитать гранулометрический состав продукта для любых условий гранулирования в аппаратах барабанного типа. Одна­ко полученные аналитические зависимости не учитывают. влия­ния теплообмена на кинетику гранулообразования в грануля­торах барабанного типа.

Аналитическое исследование ("53] процессов гранулирования в грануляторах барабанного типа, базирующееся на обобщен­ном подходе к описанию кинетики гранулирования, основано на следующих предпосылках:

все процессы гранулирования независимо от их аппаратур­ного оформления осложнены процессами тепло - и массооб-

мена;

в процессе гранулирования влажный материал контактиру­ет с теплоносителем, получая от него или отдавая ему тепло, расходуемое на испарение влаги и нагрев (или охлаждение) материала.

Таким образом, изменение агрегатного состояния гранули­руемого материала приводит к изменению его температурного поля. В свою очередь температурное поле определяет термо­диффузионный поток влаги, препятствующий массопереносу, вызываемому градиентом концентрации влаги [54].

При решении частных задач описания законов роста гранул такое взаимосвязанное влияние процессов тепло - и массообме - на и процесса гранулирования (при соответствующих краевых условиях) возможно оценить лишь при разработке физических моделей, определяющих механизм и кинетику гранулирования.

Для аналитического описания закона роста гранул в аппа­рате барабанного типа разработана [21] следующая физиче­ская модель роста гранул:

Рис. 2.1. Модель роста гранул в гра-
нуляторе барабанного типа:

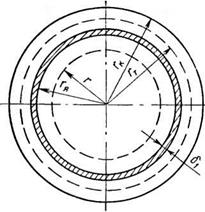гя — радиус частиц ядра; г — текущий ра-
диус частиц ядра; гт — текущий радиус
гранулы; гк — конечный радиус гранулы;
бі — толщина пленки жидкости

на сухое ядро — центр гра - нулообразования, имеющее сферическую форму, наносит­ся сплошная пленка жидкой фазы (рис. 2.1);

рост гранулы происходит за счет наслаивания сухих тон­ких частиц на окруженное жидкой пленкой ядро;

предельный размер гранулы определяется удерживающей способностью смоченного ядра. Кроме того, с учетом результа­тов ранее выполненных исследований принято, что температур­ное поле в грануле однородно, не изменяется за время пребы­вания в грануляторе.

На основании принятой физической модели можно пола­гать, что влага, заключенная между сухим ядром и слоем тон­ких частиц, будет распределяться за счет разности концентра­ций между ними (рис. 2.1). При этом распределение влаги между сухим ядром и пленкой жидкости, а также между плен­кой жидкости и сухими частицами, образующими внешний слой, подчиняется одному и тому же закону одномерной сфериче­ской диффузии:

du/dx=am [ (д2и/дг2) + (2 /гди/дг)], (2.32)

где и(г, т) — влагосодержание гранулы, зависящее в общем случае от ее размера и времени; г — текущее значение радиуса гранулы.

Уравнение (2.32) удовлетворяет следующим краевым усло­виям:

На интервале 0<г<гк

и (О, т) = ия(т), и(гя, х) ипл; (2.33)

на интервале (гя+6і)<г<гк:

и(ля+6і, т)=ипл, и (г к, т) =иЯу (2.34)

где ы„ — влагосодержание ядра; гя — радиус частиц ядра; иш, — влагосодер - жанне пленки жидкости; 6і — толщина пленки жидкости; гк — конечный ра­диус гранулы.

Анализ экспериментальных данных по кинетике поглощения влаги показал, что влагосодержание частиц пропорционально ее поверхности, т. е. г2, и функция и(г, т) может быть аппрок­симирована следующими зависимостями: при 0<г<лк

и (г, т) = иЙ+ («пл — и„) (г/г„)5; (2.35)

при (/я+ві) <г<г*

и=ия+ (ц„„ - «») (гк2 - гт2)/ [лк2 — (гя+6,)2]. (2.36)

Принимаем начальное значение влагосодержания ядра рав­ным влагосодержанию ретура «р, а н„л=1.

Решая совместно уравнения (2.32), (2.35) с учетом (2.33), а затем (2.32) и (2.36) с учетом (2.34), получим уравнение для расчета скорости роста гранул в грануляторе барабанного типа:

Гк/тя=2{(1 Ч-бі/гя)2+91п [2 — (1 — ыя0)ехр(— 9ятт/гя2)]}1/2— 1. (2.37)

Так как 6і<С>я и н°я = 0, то уравнение (2.37) принимает вид: Гк/Гя=2(1+9 1п[2- ехр(— 9ятт/гя2)]},/2- 1. (2.38)

Уравнение (2.38) получено на основе рассмотрения идеаль­ного процесса роста гранул в грануляторе барабанного типа при условии неизменности их структуры, отсутствия истирания, дробления и других сопутствующих процессов, приводящих к изменению размера гранул.

С учетом процессов уплотнения, истирания, измельчения формирующихся гранул [21] аналитическое уравнение для рас­чета радиуса гранул в зависимости от времени пребывания в грануляторе барабанного типа может быть представлено в

виде:

тк=Гя(2Л/ — 1) — кг, (2.39)

где ЛГ={1+91п[2—ехр(—9атт/л2я)]}>/2, k — кинетический коэффициент исти­рания гранул (м/с), зависящий от свойств гранулируемого материала и па­раметров процесса.

Значения кинетического коэффициента истирания могут быть определены при сопоставлении идеального и реального процессов гранулирования минеральных удобрений в грануля­торе барабанного типа. Уравнение (239) можно представить в другом виде, если известны основные размеры гранулятора.

При заданных конструктивных размерах гранулятора время пребывания гранулируемого материала в аппарате определя­ется по формуле

т=0,785/>с216 Ф/<2ш, (2.40)

где De — диаметр барабана; L6 — длина барабана; Ф — коэффициент запол­нения барабана; Qm — объемный расход шихты через гранулятор.

В свою очередь объемный расход шихты через гранулятор равен:

£ш=Сс(1+д)р„(1-Ир), (241)

где Gc — производительность гранулятора по сухому продукту.

Подставляя (2.40) и (2.41) в формулу (2.39), получаем уравнение для расчета скорости роста гранул с учетом физико­механических, тепломассообменных свойств материала и конст-

Рис. 2.2. Экспериментальная (точки) и расчетная (линия) зависимости радиуса гранул аммофоса ZK от времени пребыва­ния в грануляторе т

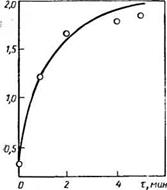руктивных размеров гранулятора:

Гк=Гя(2Л"— 1) —kx, (2.42) где N' = { 1 + 9 1п[2 — exp (— 9атВ/г„2)]},/2; В=С,785Вб2Ве Ф рн (1 — up)/Gc(1+h).

При заданном гранулометриче­ском составе исходного материала и требуемом размере гранул гото­вого продукта формула (2.42) позволяет определить основные габариты гранулятора барабан­ного типа.

На рис. 2.2 представлены расчетные и экспериментальные кривые скорости роста гранул аммофоса в грануляторе бара­банного типа. Как видно из рисунка, максимальное отклонение расчетных значений диаметра гранул на выходе из гранулято­ра от экспериментальных достигает 10%. Указанное отклонение обусловлено тем, что расчетные значения радиуса гранул по­лучены при рассмотрении идеального процесса гранулирования, который не учитывает влияние сопутствующих процессов (из­мельчения, истирания и т. п.), приводящих к изменению разме­ра гранул. На основании сопоставления расчетных и экспери­ментальных значений радиуса гранул в зависимости от времени пребывания в грануляторе получена аналитическая зависимость для расчета кинетического коэффициента k (в м/с) истирания гранул:

£ = 10~5 (ш Gc/ar)i/2,

где (о—угловая скорость вращения гранулятора; Gc—расход шихты через гранулятор; ог — прочность гранул, при расчете принимается равной проч­ности гранул готового продукта.

К этому же классу грануляторов барабанного типа отно­сятся аммонизаторы-грануляторы, в которых одновременно с процессом формирования гранул осуществляется процесс ней­трализации свободной кислоты (азотной, фосфорной), содержа­щейся в подаваемой жидкой фазе (пульпе, плаве).

Для расчета гранулометрического состава на выходе из ам- монизатора-гранулятора можно воспользоваться уравнением

(2.42) . Особенности расчета зоны аммонизации отражены в гл. 6.