ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ПЛАЗМЫ ПО ЦИКЛОТРОННОМУ ПОГЛОЩЕНИЮ В НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
А. А. Сковорода, А. В. Тимофеев, В. Н. Швилкин
Рассмотрены циклотронные колебания при немонотонном изменении магнитного поля в области, занятой плазмой. Показано, что коэффициент поглощения колебаний с частотой, несколько меньшей минимальной циклотронной (или большей максимальной), существенно зависит от температуры плазмы. В силу этого появляется возможность определения температуры плазмы по измерениям коэффициента поглощения. Предлагаемая методика испробована на простейшем > плазменном объекте - плазме газового разряда. Результаты хорошо согласуются с данными, полученными зондовым методом. Мы полагаем, что предлагаемый метод определения температуры плазмы может быть использован и в термоядерных системах.
Иавестен способ определения температуры плазмы по допплеровскому уши ре кию линии циклотронного поглощения (см., например, Е1]). Его можно использовать при слабой неоднородности магнитного поля, когда изменение циклотронной частоты б©, в области, запятой плазмой, мало по сравнению с характерной величиной допплеровского сдвига кУт. Здесь к — волновое число колебаний, Ут — тепловая скорость электронов (для определенности рассматривается электронная компонента плазмы).
Системы, предназначенные для магнитного удержания плазмы, как правило, характеризуются обратным соотношением между бсов и кУт (б©в>Л1^г). В этом случае, коэффициент поглощения вообще не зависит от температуры электронов и определяется градиентом магнитного поля и плотностью плазмы. (Коэффициент поглощения был рассчитал в [*], см. также обзорную работу [3], и экспериментально определен в [4].) Однако это утверждение справедливо лишь, если точка циклотронного резонанса, в которой выполняется условие ©=©,(2), не является точкой экстремум« магнитного поля.
В настоящей работе показано, что если магнитное поле в пределах системы имеет экстремум, то коэффициент поглощения колебаний с частотой, близкой к экстремальной циклотронной, существенно зависит от температуры электронов. Следовательно, результаты экспериментального измерения коэффициента поглощения содержат информацию об электронной температуре и, вообще говоря, позволяют определить ее величину.
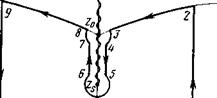
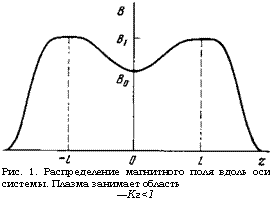
Предположим, например, что магнитное поле имеет минимум в некоторой точке, лежащей в области, занятой плазмой (см. рис. 1). Такая конфигурация магнитного поля, как известно, характерна для адиабатических ловушек. Пусть частота колебаний © меньше минимальной циклотронной <о, о, но разность ©,<>—© невелика, так что ©*<>—ш^кУт. Хотя в этом случае резонансное условие ©^©.(г) нигде не выполняется, с волной будут взаимодействовать электроны, движущиеся ей навстречу, для которых за счет допплеровского сдвига частота волны ©'*=©—кУ сравнивается или
Превышает Шео - Очевидно, что с уменьшением о) число электронов, взаимодействующих с волной, а следовательно, и коэффициент поглощения г] (со) будут падать, причем закон спадания должен зависеть от температуры электронов. Таким образом, по характеру зависимости г(ы) мы можем судить об электронной температуре. Разумеется, электронная температура может быть определена и по единичному измерению коэффициента поглощения при некотором значении CD. Однако для этого необходимо дополнительно точно знать величину соео, что подчас весьма затруднительно ввиду, например, диамагнетизма плазмы.
|
Рис. 1. Распределение магнитного поля вдоль оси системы. Плазма занимает область —Кг<1 |
 Следует отметить, что в неоднородном магнитном поле наряду с эффектом Допплера к размытию линии циклотронного поглощения приводит также эффект конечности времени резонансного взаимодействия.
Следует отметить, что в неоднородном магнитном поле наряду с эффектом Допплера к размытию линии циклотронного поглощения приводит также эффект конечности времени резонансного взаимодействия.
Действительно, при резонансе в неоднородном магнитном поле, когда резонансное условие со=
=cd,(z), строго говоря, выполняется лишь в одной точке, электрон взаимодействует с колебаниями некоторое конечное время б£ (см., например, [3]). За это время электрон не сможет «различить» колебания, частота которых отличается от й>в0 на 6©«6f-1. Эффекты, связанные с конечностью времени резонансного взаимодействия, учитывались в [3] при рассмотрении устойчивости плазмы в адиабатической ловушке, а также в [в], где исследовалось циклотронное поглощение электронов в установке конечного размера.
В теоретической части настоящей работы рассчитан коэффициент поглощения колебаний с со<о)е0. Вычисления произведены в предположении т)<1, когда влияние резонансного взаимодействия на распространение колебаний можно учитывать в качестве малой поправки. Фактически нами рассчитан лишь «хвост» линии циклотронного поглощения при достаточно больших значениях разности Дсо=йь0—©. Однако для определения температуры электронов этого вполне достаточно.
Непосредственно в эксперименте определяется не коэффициент поглощения tj, а коэффициенты прохождения т и отражения р. Затем коэффициент поглощения вычисляется по формуле т|=1—т—р. В нашем случае отражение колебаний вызывается неоднородностью среды, по которой они распространяются (неоднородность плотности, неоднородность магнитного поля). Рассмотрение показывает, что коэффициент отражения может быть надежно рассчитан лишь при выполнении условия С=(аРгЬ/ /(cdAcd)'ac<1, где о)Р — плазменная электронная частота, L — характерный масштаб изменения магнитного поля. Фактически эксперименты проводились в условиях, когда коэффициент отражения был пренебрежимо мал.
Во второй частп работы описаны эксперименты по определению температуры электронов в газовом разряде в неоднородном магнитном поле. Магнитное поле возрастало в направлении вдоль оси системы от центра к краям области, занятой плазмой. Разрядная трубка помещалась в волновод, в котором возбуждались электромагнитные колебания. Измерялся коэффициент поглощения колебаний в функции от минимального значения магнитного поля. (Используя то обстоятельство, что в выражение для
коэффициента поглощения входит не сама частота со, а разность Да)=соео— со, мы, при фиксированном значении со, меняли величину магнитного поля.) По закону спадания коэффициента поглощения с ростом со,0 определялась электронная температура. Полученные значения температуры хорошо согласуются с результатами зондовых измерений. Для проведения экспериментов мы выбрали газовый разряд, поскольку газоразрядная плазма является наиболее простым и удобным объектом исследования. Вместе с тем мы не видим принципиальных препятствий для использования предлагаемого способа в термоядерных системах.
1. Теория
А. Распространение колебаний
![]() Рассмотрим электромагнитные колебания, распространяющиеся в плазме вдоль магнитного поля. Если электрический вектор колебаний вращается в ту же сторону, что и электроны в магнитном поле, но резонансное условие G)=G)r(z) нигде не выполняется, tq волновое уравнение принимает следующий вид (см., например, [2*3]):
Рассмотрим электромагнитные колебания, распространяющиеся в плазме вдоль магнитного поля. Если электрический вектор колебаний вращается в ту же сторону, что и электроны в магнитном поле, но резонансное условие G)=G)r(z) нигде не выполняется, tq волновое уравнение принимает следующий вид (см., например, [2*3]):
~-------------------------- г)я.-0. ()
Сг со (со* (я) —со) /
Здесь используется декартова система координат, ссь z которой направлена вдоль магнитного поля, зависимость циклотронной частоты от координаты z выбрана в виде со, (2) =(Deo(l+z7L2), частота колебаний считается близкой К СО, Of CD<d),o, Е-=ЕХ— iEy=E - (z) e~imt. При низкой плотности плазмы, когда выполняется условие 1, второе слагаемое в скобках в (1) может учитываться в качестве малой поправки. Пренебрегая в первом приближении этим слагаемым, для волны, распространяющейся слева направо, получаем E-(z)&e'"x/c. Если выполняется обратное условие, С>1, то влияние плазмы может быть учтено в квазиклассическом приближении. В этом случае имеем:
*-(x)«*-»exp(jj*(*)&), fe(z) = 7-(1 + - tt>-(tt> ^i,)_a))) /‘ • <2)
Б. Поглощение колебаний
Как было отмечено во Введении, электроны могут обмениваться энергией с колебаниями, даже если резонансное условие co=co,(z) не выполняется нигде в пределах системы. Будем считать, что разность частот До)=со,0—со достаточно велика, так что резонансные эффекты малы. В этом случае в первом приближении можно считать, что колебания имеют вид бегущей волны, а резонансные эффекты учитывать по методу последовательных приближений.
Уравнение движения электрона в поле электромагнитной волны круговой поляризации представим в виде
ЕЕ-
V - + 1сов (2 (t)) ---------- exp (— Ш 4- ikz (t)). (3)
Т
Здесь V-=VX—iVv, релятивистские эффекты не учитываются. Из уравнения (3) получаем
F_ Jdt' exp icof' + ikz(t') + i J сd9(t")dt"^ . (4)
Считая скорость движения электрона вдоль магнитного поля постоянной, из (4) находим изменение бУ'- при прохождении через минимум магнитного поля (см. также, например, [7]):
Здесь А! — функция Эйри, V — продольная скорость электрона, ф — фаза колебаний в момент прохождения минимума магнитного поля. При получении (5) волновое число для простоты считалось постоянным. Для того чтобы учесть зависимость к от координаты в (5), следует произвести замену
Функция Эйри экспоненциально затухает при положительных значениях аргумента и осциллирует при отрицательных, причем амплитуда осцилляций спадает по степенному закону с ростом модуля аргумента. Если аргумент функции Эйри отрицателен, то это означает, что с учетом допплеровского сдвига частота колебаний о/—©—кУ превышает ©.о. Очевидно, что такие колебания могут взаимодействовать с ларморовским вращением электрона. Ввиду того что зависимость циклотронной частоты от продольной координаты имеет вид параболы, резонансное условие ©'=©,(2) будет выполняться в двух точках, расположенных симметрично по разные стороны от минимума магнитного поля. При определенных расстояниях между резонансными точками фаза циклотронных колебаний в моменты их прохождения будет различаться на (2/Н-1)я. В этом случае вклады резонансных точек в б У - будут взаимно погашаться. С увеличением ©'= =©—кУ резонансные точки удаляются от минимума магнитного поля, что приводит к сокращению резонансной зоны. В соответствии с [3] размер резонансной зоны равен
V тЛ 1 1 + (-г)
|
62 ж |
![]()
|
ІВ ш' / г. (7) |
![]() Со« Ь I
Со« Ь I
/ 1 ЛВ -‘/> ш' і г.
Г* ( В йг) . ’ ш,0 ( и
Где ^ — точка резонанса, гв=Ут/а>ео, Ут=(2Т'/т)Чг — среддяя скорость теплового движения электронов вдоль магнитного поля. Поскольку время резонансного взаимодействия сокращается, то V - меняется на меньшую величину. Этим объясняется уменьшение амплитуды осцилляций с ростом модуля аргумента функции Эйри.
При положительных значениях аргумента функции Эйри ©'<©*,, и обмен энергией между колебаниями и электронами обусловлен эффектами конечности времени резонансного взаимодействия. Характерный масштаб спадания б У'- с уменьшением ©' равен обратному времени пролета электрона через резонансную зону при ©'=©,<>.
При прохождении электрона через минимум магнитного поля энергия ларморовского вращения изменяется на
1/2т(|6Г-|2+НеГ-6Г-в). (8)
При усреднении по времени второе слагаемое в скобках пропадает и для
Количества энергии, йоглощаемого электронами в единицу времени, по
Лучаем следующее выражение:
6е = 72/71 ],<гГп„/0(У)Л6Г_|г. (9)
Из-за довольно сложной зависимости бУ'-(У') (см. (5)) интеграл (9) удается вычислить, лишь сделав некоторые упрощающие предположения. Допустим сначала, что характерный масштаб изменения б У-, равный о)/с“1(гУЬ)1/*> мал по сравнению с тепловой скоростью электронов Ут - Усредняя по быстрым осцилляциям |6Г-(У)|2, положим
167- {V) 1(©-©ео-кУ),
Жг я2 / еЕг 1 / Ь 4/* /ллч
0(х)=1 (х>0) или 0(х)*=О (х<0). Это представление фактически означа - ет, что с колебаниями взаимодействуют лишь те электроны, для которых частота колебаний с учетом допплеровского сдвига превышает й>е0. Пред - полагая распределение электронов по скоростям максвелловским, из (9) получаем:
|
Л17* иРгУ |
Здесь У'в^До/Л. Коэффициент поглощения колебаний ц равен отношению энергии, поглощаемой в единицу времени, к потоку энергии в колебаниях. Используя выражение для потока (см., например, [“]), получаем
2./,3./,Г(7,) с2............................................................................................ .
. / а> ©» / © Ч
*-тах(т,— (—) ).
Если выполняется обратное условие, сок~1(ге/Ь)г/*^>Ут, то эффект ко - нечности времени резонансного взаимодействия преобладает над эффектом Допплера. В этом случае характерный масштаб изменения величины ІбУ'-І2, рассматриваемой как функция V, всюду в области У^>УТ значительно превышает Ут. Вычисляя (9) по методу перевала, приходим к еле* дующему выражению:
Я* сор2Ь / о> х1/» / / Ь® г/х Д© ,
Ч"в*пЕ?-Ы ехрг3 2 (тг) —)■ (13>
В. Отражение колебаний
Можно показать, что отражение, связанное с резонансным взаимодействием, пренебрежимо мало, и поэтому коэффициент отражения может быть найден с помощью консервативного уравнения (1). При параболической зависимости магнитного поля от координаты это уравнение не сводится к стандартным, и поэтому для вычисления коэффициента отражения р приходится использовать приближенные методы. -
Предположим, что выполняется условие С<1. В этом случае «плазменное» слагаемое в (1) может быть учтено как малая поправка в рамках так называемого борновского приближения (см., например, [*]). Стандартная процедура дает:
Л* а>тЧг [ о>Ь
Р“т^-ехр(-4— (-гг) )• (14>
При С» 1 становится справедливым квазиклассическое приближение. Для
1т г
|
|
|
В |
|
10 |
|
1 |
|
О |
![]() ЯЄ2
ЯЄ2
Рнс. 2. Плоскость комплексного переменного Г Для уравнения (I). Решение продолжается из области Ие г>0 в область Ие г<0 по пути 1-10
Вычисления коэффициента отражения в этом случае будем пользоваться методом, предложенным в [|0]. В соответствии с [10] рассмотрим аналитическое продолжение уравнения (1) на плоскость комплексного переменного г. Квазиклассическое приближение нарушается в точках г0 и га, в которых волновое число к (г) обращается соответственно в нуль и бесконечность. Проведем из этих точек линии, на которых меняется лишь действительная часть комплексной «фазы» квазиклассического решения. На рис. 2 это линия и отрезок Поскольку точка г8 является точкой ветвления решения, из нее должен выходить разрез. В данном случае его удобно провести вертикально вверх (волнистая линия). Интересующее нас решение при больших положительных значениях ъ имеет вид волны, бегущей направо. Продолжим его налево по линии 1—10. В окрестности точек г0 и г«5, где нарушается квазиклассическое приближение, уравнение (1) сводится к уравнениям Бесселя. С их помощью находим, что обход точек г0 и г«5 приводит к изменению квазиклассического представления решения — в нем появляются слагаемые, соответствующие отраженной волне. На линиях действительной фазы они имеют амплитуду, сравнимую с амплитудой «падающей» волны. Однако на участке 9—10 «падающая» волна экспоненциально нарастает, а «отраженная» спадает. В результате коэффициент отражения оказывается экспоненциально малым:
|
|
|
|
|
А |
|
(15) |
Здесь Ф — набег фазы квазиклассического решения на отрезке ъ&ь, А — изменение мнимой части фазы при переходе с действительной оси на линию АВ, К', Е', Е — полные эллиптические интегралы (см., напри-
Мер, [“]).
Коэффициент отражения обращается в нуль при Ф=/гя. В этом случае волны, «отраженные» точками г0 и погашают друг друга. Аналогичное явление известно в оптике под названием просветления, а в теории рассеяния электронов на атомах называется эффектом Рамзауэра (см., напри - мер, [“]).
Мы аппроксимировали зависимость магнитного поля от координаты параболой. Эта аппроксимация годится при малых значениях Ъ, т. е. в центре системы, но, очевидно, нарушается в области пробок. Более близкой к реальной будет зависимость
Я(2) = Я0[1+-^(1 + а-^-)“‘] . (16)
Коэффициент отражения в этом случае может быть получен из (15) переопределением:
(1<)
/ Дсо '1г г / До) Юр2 1 ~ъ
Н,+“—) [1+“(—-
Для того чтобы найти новое значение для коэффициента отражения (14). его следует представить в виде
Р= (п/2)2 (1—Ь02/Ь2) ехр (-АМс) (18)
И затем произвести те же замены. Если А по порядку величины равно единице, что характерно для реальных ловушек, то (15) может существеппо измениться, в то время как (14) практически не меняется. Последнее следует из условия сор2/со2<1, которое обеспечивает выполнение неравенства
1. Это различие между (14) и (15) обязано следующему обстоятельству. При 1 колебания отражаются областью, в которой коэффициепт
Уравнения (1) меняется наиболее резко, т. е. окрестностью минимума маг
Нитного поля. Если же С>1, то отражение происходит в области, где параметр квазиклассичности K~2dk/dz максимален. Ввиду возрастания К при 2-^0 эта область не обязательно совпадает с окрестностью начала координат. Таким образом, для расчета коэффициента отражения при С> 1 следует принимать во внимание реальный профиль магнитного поля. Помимо того, необходимо учесть также отражение от градиента плотности плазмы. Все это делает расчеты весьма затруднительными.
2. Эксперимент
А. Описание установки
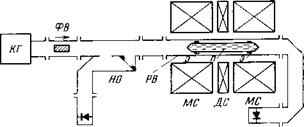
Опыты проводились на установке, изображенной на рис. 3. Плазма создавалась в стеклянной цилиндрической трубке (П) с помощью высоко частотного генератора с симметричным относительно земли выходом. Напряжение с генератора прикладывалось к двум тонким медным электродам (Э), охватывающим трубку снаружи вблизи от ее торцов. Их ширина
1,5 См, толщина 0,02 См. Мощность генератора 100 Вт, его частота 40 Мгц. Торцы разрядной трубки представляли собой конусы вращения высотой 3 См. Длина однородной части трубки 50 См, ее диаметр 2,8 См. Трубка наполнялась гелием, аргоном, криптоном и парами ртути. Диапазон рабочие давлений изменялся от 5 • 10“2 до 1 • 10~4 Мм рт. ст. Параметры плазмы определялись с помощью двойного электрического зонда, расположенного перпендикулярно оси трубки. Длина активной части зондов составляла 3 Мм, диаметр зондов —0,1 Мм. Зондовые измерения показали, что температура электронов изменяется приблизительно от 1,5 до 20 Эв, концентрация плазмы не превышает 5-109 См~3. Степень ионизации газа —10“*
|
Рис. 3. Схема экспериментальной установки: КГ — кли - стронный генератор, ФВ - ферритовый вентиль, НО - Направленный ответвитель, ДГ - детекторная головка, РВ — разборный волновод, Э — электроды ВЧ, П — плазма в диэлектрическом баллоне, МС — многосекционный соленоид, ДС — дополнительный соленоид |
Разрядная трубка помещалась внутри прямоугольного волновода (РВ) Ечением 72X34 Мм2, в котором возбуждалась электромагнитная волна ти - 1А Я10 на фиксированной частоте 2,92 Гец от шшстронного генератора КГ) мощностью 0,5 Мет. Паразитная девиация частоты генератора св - тавляла 1*10~2%. В работе использовалась амплитудная модуляция зон - шрующего плазму GB4 сигнала на частоте 1 Кгц.
Магнитное поле пробочной геометрии создавалось с помощью много - екционного соленоида {МС) общей длиной 100 См. Типичное распреде - iemie магнитного поля вдоль оси плазменного столба показано на рис. 1. Ьазма при этом занимала область —Kz<L. Максимальная величина маг - пгтного поля в опытах достигала 2 Кгс. Неоднородность поля по сечению рубки не превышала 0,2%. Стабильность магнитного поля составляла 11%. Наибольшая величина пробочного отношения R=Bi/B0 в экспери - [ентах доводилась до значения, равного 1,7. Зависимость магнитного поля т координаты Z в области минимума B(Z=0) с хорошей степенью точности ожно было аппроксимировать выражением B=B0(L+Z2/L2). В условиях пыта значение L изменялось от 10 до 20 См. При проведении эксперимен - ов была предусмотрена возможность небольшого (порядка 4%) локаль - юго изменения магнитного поля с частотой £2=50 Гц в области минимума аспределения B=F(Z). Это достигалось с помощью включения дополни - ельной секции соленоида (ДС), показанной на рис. 3. При этом минималь - ая электронная циклотронная частота менялась по закону
EBg
С)ео (Оео I COS
Тс
Измерение переменного магнитного поля Bg осуществлялось магнит - ым зондом. Сигналы с этого же зонда синхронизировали горизонтальную азвертку двухлучевого осциллографа С8-2. На вертикальные входы осцил - ографа поступали сигналы с детекторных секций (ДГ), проходящиече -
Оз измерители отношения сигналов В8-6.
Б. Результаты измерений
На рис. 4 показана осциллограмма выходного сигнала с детекторной повки ДГ-2. Она характеризует зависимость мощности прошедшей тектромагнитпой волны при фиксированной частоте от переменного маг - лного поля BgCosQt, создаваемого дополнительным соленоидом. За ремя развертки, отмеченное на осциллограмме цифрами 1-*4, вспомо-
Гательное магнитное поле изменяется от — Вй до +ВЙ. При этом величина минимального стационарного магнитного поля В0 выбиралась из условия электронного циклотронного резонанса в минимуме магнитного поля и равнялась Во=тса)/е=1,04 кгс. Пробочное отношение Д=1,3 (£=14еле). Участки огибающей, отмеченные на осциллограмме рис. 4 цифрами 1—
2, 2—3 и 3—4, отвечают, соответственно, следующим условиям: 0)>0)ео> СО«63*о, 0)<0)ео. Участок
1—  2 кривой характеризуется наличием двух разнесенных в пространстве резонансных точек. Участок 2—3 характеризуется отсутствием точек точного циклотронного резонанса (ш=бЗе0). Этот участок осциллограммы позволяет получить профиль линии циклотронного поглощения в плазме в об - л, ласти расположения минимума
2 кривой характеризуется наличием двух разнесенных в пространстве резонансных точек. Участок 2—3 характеризуется отсутствием точек точного циклотронного резонанса (ш=бЗе0). Этот участок осциллограммы позволяет получить профиль линии циклотронного поглощения в плазме в об - л, ласти расположения минимума
Рис. 4. Осциллограмма, характеризующая магнитного поля. Участок 3-4 ос -
Изменение коэффициента прохождения т
От магнитного поля Вл совШ циллограммы отвечает условиям,
При которых циклотронный резонанс в плазме уже не имеет места и электромагнитная волна распространяется через нее без поглощения.
Одновременно с проходящей мощностью волны в работе регистрировалась также отраженная мощность с помощью направленного ответвителя (НО). Опыты показали, что отраженная мощность зависит от концентрации электронов и величины Ь. Отражение волны становится заметным лишь при концентрациях электронов, больших 1-10® сж“ и значениях Ь, меньших 10 см. Однако при этом отраженная мощность не превышала 10% от мощности падающей волны. В условиях, при которых получались осциллограммы, аналогичные изображенной на рис. 4, отраженный сигнал был пренебрежимо мал. Последнее обстоятельство позволяет использовать осциллограмму рис. 4 для получения информации
О поглощении волны в плазме. При этом поскольку в условиях опыта можно считать, что т|=1—т, величина коэффициента поглощения мощности волны в плазме прямо пропорциональна ординате А, отсчитываемой от продолжения горизонтальной части участка 3—4 кривой, соответствующей условию т=1. Для измерения электронной температуры необходимо знание наклона зависимости 1^т) от ДсоАо. Так как т)~А, этот наклон в точности совпадает с наклоном зависимости ^ А от Ли)/со.
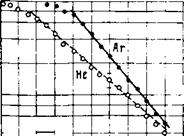
На рис. 5 приведены найденные описанным выше способом зависимости 1^Д от величины Дсо/со, характеризующей расстройку электронного циклотронного резонанса (Д со =“©,<>—со). Результаты приведены для плазмы, образуемой в гелии и аргоне при давлении 1Ю“3 мм рт. ст. Отсчет расстройки резонанса производился от точки 2, см. рис. 4. Для случая аргоновой плазмы начало отсчета До/й) на рис. 5 обозначено стрелкой. Из рис. 5 видно, что зависимости 1&Л от До/со в некотором интервале изменения значений Д со/со имеют линейный характер. Такая зависимость при фиксированной частоте о согласно формуле (13) может
|
8 |
![]()
|
О |
|
0,1 |
![]() 100
100
|
0,2 |
![]() 10
10
|
|
|
0,01 |
|
О |
|
/ |
|
/ |
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
![]()
Рис. 5. Зависимость от Аа)/(о
Рис. 6. Температуры электронов Те в плазме инертных газов и паров ртути, измеренные по циклотронному поглощению (•) И С ПОМОЩЬЮ ЗОНДОВ (О)
Иметь место в случае, если профиль линии циклотронного поглощения в минимуме магнитного поля определяется конечностью времени резонансного взаимодействия частиц с волной. Для этого, как показано в разделе 1, необходимо, чтобы выполнялось неравенство
![]()
![]() В условиях опытов
В условиях опытов
И значение В=(с3/(огУтЬг)ч Рассчитанная с учетом изменения скорости электромагнитной волны в волноводе, величина Б в экспериментах изменялась от 1,5 до 3.
Для линейного участка зависимости 1^ Д от Дю/ю, изображенной на рис. 5, выполняется условие С< 1. При этом, как следует из теоретической части работы, отражение волны может быть описано формулой (14). Расчеты по (14) показывают, что в соответствии с экспериментом отраженная мощность волны при концентрациях электронов, меньших 1 • 10* емг3, пренебрежимо мала.
При теоретическом анализе циклотронного поглощения колебаний плазма считалась бесстолкновительной. Однако в плазме газового разряда, использованной в наших экспериментах, вообще говоря, необходимо учитывать столкновения электронов с нейтральными атомами. Под их влиянием так же. как и под влиянием эффектов, описанных в предыдущем разделе, происходит уширенпе линии циклотронного поглощения. Это уширение под действием электрон-нейтральных столкновений наблюдалось в работе при давлениях выше некоторого граничного, зависящего от сорта газа. Однако уширение линии при давлениях, меньших чем
2- 10"* мм рт. ст., не обнаруживалось во всех исследованных случаях.
Знание наклона линейной части зависимости 1|?Л от Дю/ю, изображенной на рис. 5, позволяет оценить температуру электронов в плазме по формуле (13). На рис. 6 точками представлены найденные таким образом значения Те в инертных и ртутной плазмах. Изображенные на
рисунке результаты получены из усреднения по большому числу измерений при давлении 1-10"3 мм рт. ст. для различных значений параметра L. На том же рисунке для сравнения светлыми точками нанесены значения температур электронов, найденные из зондовых измерений. Как видно, результаты, полученные различными методами, близки друг к Другу.
Приведенные в работе данные получены в слабоионизованной низкотемпературной плазме газового разряда. Однако предложенный нами метод может быть использован и для определения температуры в горячей полностью ионизованной плазме.
|
Поступила в редакцию И февраля 1977 г. |
![]() Московский государственный университет им. М. В. Ломоносова
Московский государственный университет им. М. В. Ломоносова