К ВОПРОСУ О ПОСТОЯНСТВЕ АДИАБАТИЧЕСКОГО ИНВАРИАНТА ПРИ ИЗМЕНЕНИИ ХАРАКТЕРА ДВИЖЕНИЯ
А. В. Тимофеев
Рассмотрено движение заряженной частицы в пространственно-периодической волне, амплитуда которой возрастает со временем. Вычислено изменение адиабатического инварианта при захвате частицы волной. Полученные выражения пригодны также для описания движения маятника переменной длины в поле силы тяжести при переходе от вращения к колебаниям возле точки устойчивого равновесия.
1. Известно, что движение механических систем с медленно меняющимися параметрами характеризуемся величиной, которая сохраняется с высокой степенью точности — адиабатическим инвариантом (см., например, [Ч). Это утверждение справедливо как при финитном движении изображающей точки на фазовой плоскости, так и при инфинитном. Однако в ряде случаев оказывается необходимым исследовать переход от одного вида движения к другому. Так, например, заряженные частицы, движущиеся в пространственно-периодической волне, амплитуда которой возрастает со временем, могут захватиться волной. При этом на фазовой плоскости их траектории перейдут из области инфинитного движения в область финитного (см., например, [2]). Эта задача имеет простую механическую аналогию — движение маятника переменной длины в поле силы тяжести, причем колебания маятника относительно положения равновесия соответствуют финитному движению, вращение — инфинитному.
Помимо вышеупомянутых имеется и ряд других задач, для решения которых необходимо проанализировать переход от одного вида движения к другому. К ним, в частности, относятся некоторые задачи небесной механики (см., например, [3]), а также задача о движении заряженных частиц в открытых магнитных ловушках в присутствии электромагнитных колебаний I4, *].
Одной из первых работ, в которой рассматривался вопрос о постоянстве адиабатического инварианта при изменении характера движения, является работа Беста [2]. В ней (см. также [*]) на основании теоремы Лиувилля был сделан вывод о том, что в нулевом приближении по параметру е=(й)т)_1<1 адиабатический инвариант остается неизменным. Здесь ю — характерная частота колебаний заряженной частицы в поле волны электрического потенциала, т — характерное время изменения амплитуды волны. В то же время численное интегрирование уравнений движения, проведенное в I2] в одном частном случае, показало, что адиабатический инвариант меняется на малую величину порядка е. Численные расчеты изменения адиабатического инварианта при захвате заряженной частицы волной нарастающей амплитуды были проведены в [7]. Результаты расчетов обсуждаются в тексте статьи.
В настоящей работе, как и в [2- 7], вопрос о постоянстве адиабатиче
Ского инварианта рассматривается на примере задачи о движении заря« женной частицы в волне электрического потепцпала переменной амплитуды. С точностью до величин порядка е включительно найдены траектории частиц на фазовой плоскости поблизости от сепаратрисы, разделяющей области финитного и инфинитного движений. Знание траекторий
Позволило получить аналитическое выражение для изменения адиабатического инварианта при переходе траектории через сепаратрису.
2.
|
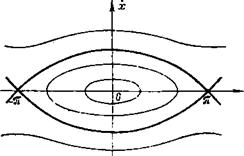
Траектории частиц на фазовой плоскости при 8=0. Сепаратриса, разделяющая области финитного и инфинитного движений, обозначена жирной линией |
![]()
 Рассмотрим движение заряженной частицы в гармонической волне электрического потенциала, амплитуда которой меняется со временем. В системе координат, движущейся вместе с волной, электрический потенциал имеет вид
Рассмотрим движение заряженной частицы в гармонической волне электрического потенциала, амплитуда которой меняется со временем. В системе координат, движущейся вместе с волной, электрический потенциал имеет вид
<р (х, T) 0А (T) (1—Cos Кх),
Где А (T) — безразмерная амплитуда, К — волновое число. Если в уравнении движения частицы заряда Е перейти к безразмерным координатам ХКх-+х, Kt(M/EQ)O)V*-*“F, То оно примет следующий вид:
Х+А (г)Sins—0. (1)
Будем считать, что амплитуда колебаний медленно меняется со временем Л(£)=1+е£, где е<1. На небольших отрезках времени решение уравнения (1) должно иметь вид ряда по степеням е. Поставим перед собой задачу нахождения двух первых членов этого ряда. Член, пропорциональный е°, описывает решение стационарного уравнения (1) при А (T) =Const. Оно, как известно, выражается через эллиптические функции (см., например, [*]). Однако эти общие выражения весьма трудно использовать для нахождения следующего приближения. Поэтому мы не будем их приводить, а для того чтобы составить общее представление о характере движения, используем фазовую плоскость (см. рисунок). На ней можно выделить области финитного и инфинитного движений. Их разделяют траектории, проходящие через гиперболические точки (±л, 0). Частицы, траектории которых фннитны, принято называть захваченными волной, частицы с инфинитными траекториями — пролетными. Энергия пролетных частиц удовлетворяет условию
PF=*1/2I2+1—Cos £>2,
У захваченных частиц W<2. Для дальнейшего существенно, что при критическом значении энергии W—2 решение стационарного уравнения (1) с е=0 имеет сравнительно простой вид:
Х0 (T) =4 Arctg Е(—Я, (2)
В окрестности сепаратрисы (|TF—2|<1) решение уравнения (1) слабо отличается от (2) :
X(T) ^Xo(T) +Xia(T) +X„(L), Где XIa. Xir — Поправки к решению, связанные соответственно с учетом разности W—2=^0 и изменения амплитуды A(T). Эти поправки могут вычисляться независимо:
Xix(T) =A(Sh T+T Ch“1 T)+A' Ch”1 F,
(3)
Xit(t) = —(—shfthf+f2 ch“1 *)•
В (3) введено обозначение: А=1и(УУ—2). Последнее слагаемое в этом уравнении. пропорциональное сс', пе дает вклада в энергию. Оно описывает смещение начала отсчета времени, и в дальнейшем мы не будем его учитывать.
Траектория, найденная нами, описывает тт0
 Дв«з«ещ, е
Дв«з«ещ, е
№(1) =2(1+2а-{-ег-е * ()
В окрестности гиперболических точек (±л д* нимает вид ’ 1 РС1цеаце ^
МО *-я+4е,-|/4 (а+е/2) в-1
Х+ (0 «л-4е-*+72 (а—е/2) в*.
Здесь знаки минус и плюс отмечают предстаще В окрестности точек (—л, 0) И (л, 0). “ НИЯ’ СЦр^
Из (6), (7) следует, что если 1*1 »1, то слагаемые ППп ^ Малым величинам а, в, экспоненциально возрастают. Цп выйти за рамки метода последовательных приближениями |*|»1, то траектории должны проходить близко от гипербол ^ 6 т. е. в области, где уравнение (1) можно линеаризовать по ^8*Хъ' Если одновременно выполнено условие 81 £| <1, то решение ладного уравнения (1) дается выражением '
:г(*) ±п=Схе1+С, е~
Т. е. совпадает по виду с (6), (7)
Таким образом, выражения (2) —(4) дают решения уравненц справедливые для всего цикла движения частицы. Здесь под Тп»^ понимаем движение пролетной частицы на отрезке (—я, я) и запав ной — от одной точки поворота до другой. Отметим также, что выражвд (2) — (4) могут быть продолжены на другой цикл движения.
3. В нестационарном случае условие захвата частиц волной имеяка ¥^)<2Л(£). Из выражения (5) следует, что частнаы с |а|<е/2,яш - щиеся «пролетными» при Х=—Л, Захватываются волной, Не успеваядогц На фазовой плоскости до линии Х=л (для определенности рассмтрш- ются частицы, скорость которых положительна;. Усмотрю!, няется адиабатический инвариант при таком перелоде. Адиа * ^
Инвариант, как известно, характеризует Квазипериоднческое Период которого Т изменяется на величину за вРемя^етвор»я1
Выражений (2) —(7) нетрудно найти, что это Условие Степ^
Если |а|>е, т. е. при движении по траекториям, в доста удаленным от сепаратрисы. В этой области aдIIa^|aTИЧeд0дЧepкнe«•,1' изменяется экспоненциально медленно: /—ехр (— | сх! / е) - нь£М ряд"*.1 этим свойством обладает выражение, Являющееся ^есь° удается ва1* степеням е<1 (см.,, например, [*])• Практически оиыч ^
Лишь один-два члена ряда. Производные УкорочепииГ0 Имеют соответственно порядок е/ |а| и (г/а)2. очяость® Д°4,1
Для уравнения (1) адиабатический Инвариант С т порядка е был вычислен в [*]. Приведем эти выра/К^вИ * ^ ^
°(^ ( ))“ I 8 М (0)»(Е (Л) + (Л*-1) К (Л)) •
Л(*.TF. il(*))- Ук), *7‘ «
Ш8П(») А К{к)Е{у к)_щк)К(у'к), с)1Я
° Оценки показывают, что учет нелинейных членов в производить в рамках следующих приближений по е.
Здесь K=(W/2A)'12, У=агсSia(A:“1 SinХ), К, Е — эллиптические интегралы первого и второго рода. Их значения при первом аргументе, равном я/2, обозначены как К, Е. Отметим, что Л обращается ч нуль при х=±я для пролетных частиц и в точках поворота (х*±агс Sin К) — для захваченных.
В окрестности сепаратрисы (к—1|<1) выражение (8) приобретает простой вид:
/,»4[2+(fc-l)ln-jjij|- + (*-l)+e*]. (10)
Вычислим, насколько меняется эта величина при переходе частицы из пролетных в захваченные. Из (6) следует, что частица проходит линию х=—я в момент времени
—■Т*Ш-
Используя выражение (5), получаем, что величина К в этот момент равна &_«1+а+е/2.
Из уравнения (7) находим момент отражения частицы от потенциального горба
При этом А:+«1+а—е/2. Поскольку /4 при T=T± Обращается в нуль, то с точностью до членов порядка е включительно изменение 1 на интервале времени (£_<£<*+) может быть получено с помощью (10):
Это выражение получено в предположении |а|<е/2, так как только в этом случае частица при £-»-£_ является пролетной (&_>1) и при T-+T+ Переходит в захваченную (Л+<1). Дальнейшая эволюция приведет к опусканию частицы на дно потенциальной ямы; причем до тех пор, пока величина |Fc—1| сравнима с е, движение не удовлетворяет условию адпабатичности. Действительно, величина К за одно прохождение между точками отражения уменьшается на е, а период движения, определяемый формально при постоянном значении К, равен
7-0/O/0W»Ln(8/|*-L|).
Аналогичная зона неадиабатического движения располагается и в области инфинитных траекторий при К—1>0.
Действуя, как и при получении (11), находим, что изменение адиабатического инварианта за один цикл движения как для пролетных частиц (к—1>е/2), так и для захваченных (А:—1<—е/2) дается одним и тем же выражением:
Л/<1,“4(а1п('^1)-в)- (12)
В выражениях (И), (12) величина а совпадает с разностью К—1, взятой в момент прохождения линии х*0. За один цикл движения она уменьшается на е. Суммируя по всем циклам, получаем
А;.2«{рь(1^)-2-
П—1
Здесь введено обозначение JJ=2a0/e, Где величина А0 характеризует тот цикл движения частицы, на котором эта частица непосредственно переходит из пролетных в захваченные, и связана с энергией в момент прохождения линии х=0 соотношением И^=2(1+2а0). С помощью (2), (5) А0 Можно выразить через значение координаты Хш точки, в которой траектория частицы пересекает сепаратрису:
E-=fsin(f)-
Используя формулы суммирования (см. I3]), а также производя ряд простых преобразований, приводим (13) к виду
Г (КП+'/г) “Р /4) 1
Д/=4е I—1+Lim ln--------------------------------------------------------------------------- F. (14)
I Г (n.+7o+Я/2) Г (/г+1/о—Я/2) cos (л Я/2) J
С помощью асимптотических представлений для Г-функций окончательно получаем
Д/=—4е 1п(2соз(жх0/е)). (15)
Наше рассмотрение относилось к случаю волны нарастающей амплитуды, когда заряженные частицы захватываются волной. Нетрудно показать, что выражение (15) остается в силе и для обратного процесса — перехода частиц из захваченных в пролетные при уменьшении амплитуды волны, когда E=dA/dt<0.
Отметим, что значения ДI для частиц, пересекающих сепаратрису в одной и той же точке, но движущихся в противоположных направлениях, одинаковы. Этот вывод следует из пространственной симметрии потенциала, в котором движутся частицы, симметрии выражения (15) по отношению к знаку Оо, а также характера связи между а0 и Х, (а0=1/2Е Sin(x»/2)).
Выражение (15) логарифмически расходится при J<x0|-*-e/2. Эта его особенность объясняется весьма просто. Если |ао|~е/2, То траектория пересекает сепаратрису поблизости от гиперболических точек, в окрестности которых частицы застревают на длительное время:
1 TOC o "1-5" h z _ / 8 е
А*~т1пи+^) пРиа»*-Т’
1 _ / 8 е
Д* « — 1п( ------------ ; —- ) При Оо « —
2 —а0+е/2 / 2
(см. выше). За это время площадь области, ограниченная сепаратрисами, увеличивается на 8еД£ (см. (8)). Вместе с ней возрастает и адиабатический инвариант, который приближенно равен половине этой площади.
Следует отметить, что выражение (15) становится неточным, если значение |оо| очень близко к е/2. Действительно, мы предполагали, что время, затрачиваемое на один цикл движения, мало по сравнению с е“!. Это предположение нарушается при 1— |2а0/е | ^е~1/в, когда в соответствии с (15) Д/ становится по порядку величины сравнимым с единицей. Однако если считать, что частицы распределены равномерно по фазовой плоскости, то доля частиц, для которых наше рассмотрение оказывается несправедливым, будет экспоненциально малой: ~е~и
Интересующая нас проблема анализировалась также в работе [7] численными методами. При | ссо | <е/3 оба подхода даюг практически один я
Тот же результат[57]. В большей части интервала е/3<|а„|<е/2 количес венно результаты также оказываются весьма близкими. Однако они ра личаются качественно в двух отношениях. Во-первых, значения А/, ра считанные в [7], конечны даже при |а0| =е/2. Во-вторых, численные ра четы дают различные значения А/ для частиц, пересекающих сепаратрис с различными знаками скорости. Первое из этих различий обусловлен самой природой численных расчетов. Действительно, численные метод, позволяют проанализировать поведение системы лишь на конечных пр< межутках времени. Поэтому в [7] считалось, что амплитуда колебанв меняется в течение некоторого конечного времени AT. Однако Частин С достаточно малым значением разности е/2— |<х0 J За это время могут г, успеть пройти зону неадиабатичности. В результате рассчитанные значн ния А/ окажутся заниженными. Отметим, что границы зоны неадиабати ности невозможно определить точно. Следовательно, даже для чаетш пересекающих сепаратрису вдали от гиперболических точек, Результаті* Расчета должны зависеть от способа задания зависимости амплитуды вол ны от времени и поэтому не имеют универсального характера.
Различие в значениях А/ для частиц, пересекающих сепаратрису с раз личными знаками скорости, возможно, обязано существенному упроще нию, использованному в [7]. А именно, в этой работе адиабатические инвариант отождествлялся с нулевым членом разложения точного выра жения по е (см. (8), (9)). Поскольку само изменение адиабатического инварианта по порядку величины равно е, то расчеты, произведенные в [7], строго говоря, следует признать некорректными. Не исключено, чт» именно с этим обстоятельством связано расщепление зависимости АI от е Действительно, слагаемое порядка е антисимметрично по скорости (см (9), а также работу Беста [*]). Возможно, что его учет устранил бы рас щепление.
Поступила в редакции 26 апреля 1978 г.