Optimizing the Tracking System
The main task in optimizing the active component (the tracked solar collector) is to maximize the energetic gain by increasing the solar input and minimizing the energy consumption for tracking. The solar collector can be rotated without brakes during the day-light, or can be discontinuously driven (step-by-step motion), usually by rotating the collector with equal steps at every hour. Obviously, the maximum incident solar radiation is obtained for the continuous motion, but in this case the operating time of the motor is high. In order to accomplish the paper goal, we used an optimization strategy comprising two steps: designing the optimal motion law - the key idea is to maximize the incident radiation gained through step-by-step orientation, for absorbing a quantity of solar energy closed to the ideal case (continuous orientation); designing the optimal tracking mechanism - this design intends to minimize the actuating force that is needed for realizing the motion law; the optimization problem uses the dynamic model of the mechanical structure, and computes the geometrical parameters.
The step-by-step tracking strategies were formulated using optimal algorithms based on the number of steps necessary for orientation [12]. These algorithms were developed considering the correlation between the maximum amplitudes of the motion and the number of the tracking steps, aiming to the minimization of the steps number. In fact, the optimization is made by reducing the angular field of the daily motion and the number of actuating operations without significantly affecting the incoming energy. It has been demonstrated that for every month there is one day whose irradiation is equal to the monthly average: it is the day in which the declination equals the mean declination of the month [13]. Due to this consideration, a noticeable facilitation is introduced in the computing calculation, considering just the mean days of each month instead of the 365 days of the year.
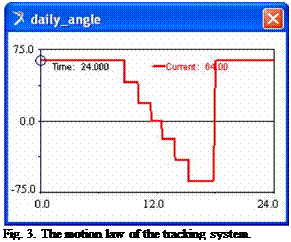
The paper presents the exemplification for the spring equinox day, the numeric simulations being performed for the Bra§ov geographic area, with the following data: the location latitude, 45.6333 N; the longitude, 25.5833 E; the day number during the year, 81; the local time for sunshine, 6.316; the local time for sunset, 18.533; the seasonal position, 42.5°. According with the orientation program developed in [12], the angular field for the daily motion in the spring equinox day is P* є [+64°, -64°] (P*=0 in the solar noon position, positive values in the morning, negative values in the afternoon). The orientation is made in 6 motion steps, as follows (local time): 8.967 (AP*=23°), 10.467 (Ap*=22°), 11.817 (Др*=19°), 13.017 (Д3*=19°), 14.367 (Др*=22°), 15.867 (ДР*=23°); the operating time for each step is 0.1 h. The system is fixed maintained in the intervals after sunshine, P* = +64°, T = (6.316 - 8.967), and before sunset, P* = -64°, T = (15.967 - 18.533). The return of the system in the initial position is made after sunset, with continuous motion in 0.2 hours. With these data, the time-history of the daily angle of the solar collector (i. e. the motion law
 |
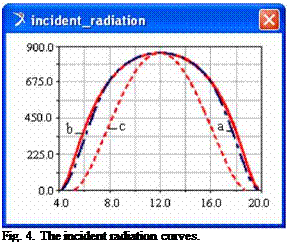 |
of the tracking system) is shown in figure 3. At the same time, in figure 4 there are presented the incident radiation curves for the following situations: a - the proposed motion law (according with figure 3), b - the maximum incident radiation that can be obtained for the continuous orientation of the panel in the maximum angular field p* є [+90°, -90°], and c - the fixed panel case. As we can see, the energy obtained by tracking the Sun with the proposed motion law is close-by the ideal case, with a minimum operating time of the motor (this is very important for the reliability & durability of the system, including the motor’s wearing).
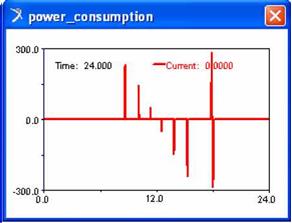
The next step in optimizing the tracked solar collector is the geometric optimization of the tracking mechanism. The optimization is approached as a problem to minimize the objective function over a selection of design variables, while satisfying various constraints on the design. The objective function is a numerical representation of the tracking system efficiency, the optimum values of this function corresponding to the best possible design. In our case, the minimization of the energy consumption for realizing the motion law is the design objective. The energy consumption (in fact, the mechanical work consumption) is obtained by integrating the power consumption curve in absolute value.
The geometric optimization of the tracking mechanism was made by using the MBS environment ADAMS, considering the following steps: parameterizing the virtual model, defining the design variables, defining the design objective, and optimizing the model. The parameterization of the tracking mechanism was made using the points that define the structural model, in fact the location of the revolute joint between collector and support. The revolute axis, which is parallel with the polar axis, is defined by the points pair A-A’ (from kinematic point of view, in A’ there is a redundant joint). For the optimization process, there was taken into consideration the global vertical coordinate of the points A-A’ (see figure 1), which has been modelled as design variable (ZA = ZA’ ^ DV_1). In fact, this coordinate (variable) defines the relative distance between the mass centre of the collector and the revolution axis.
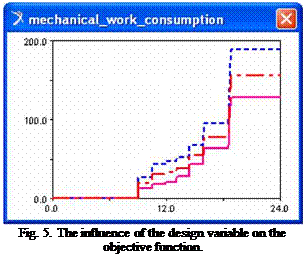
The sensibility of the objective function on the modification of the design variable is shown in figure 5 (the value range for the design variable is ±10% relative to the initial value). The solution for minimizing the consumption (the objective of the geometric optimization) is to dispose the revolute axis as close as possible to the mass centre of the collector, respecting the constructive constraints induced by the mounting of the motor.
 |
 |
In these conditions, the results obtained after the optimization process of the tracking systems are shown in the diagrams from figure 6, as follows: the control torque, the power & energy (mechanical work) consumption, and the resistant torque in the irreversible transmission when the system is in the stationary positions, for blocking the system between the motion steps (the measure units: newton, meter, hour, joule). These results are very useful for evaluating the behaviour of the solar tracking system. The energy balance can be performed considering the energy gain obtained by orientation, and the energy consumption for realizing the motion law.
Fig. 6. The results of the simulation for the mechatronic tracking system.
The application is a relevant example regarding the implementation of the virtual prototyping tools in the design process of the tracking systems used for the solar collectors. One of the most
important advantages of this kind of simulation is the possibility to perform virtual measurements in any point or area, and for any parameter (motion, force, energy). At the same time, integrating the electronic control system in the mechanical structure of the solar tracker at the virtual prototype level (i. e. the modelling in the mechatronic concept), the physical testing process is greatly simplified, and the risk of the control law being poorly matched to the real system is eliminated.
The optimization strategy based-on two operational steps (the optimization of the motion law, and the geometric optimization of the mechanical structure) leads to an efficient tracking system, without developing expensive hardware prototypes. In this way, the behavioural performance predictions are obtained much earlier in the design cycle of the tracking system, thereby allowing more effective and cost efficient design changes and reducing overall risk substantially.
The tracking system will be manufactured and tested in the Centre Product Design for Sustainable Development from Transilvania University, creating a real perspective for the research in the field. This allows a relevant comparison between the virtual prototype analysis and the data achieved by measurements.
[1] G. N. Tiwari, Solar Energy, (2002). Alpha Science Int. Ltd., Pangbourne.
[2] J. Garcia de Jalon, E. Bayo, (1994). Kinematic and Dynamic Simulation of Multibody Systems, Springer - Verlag, New York.
[3] W. Schiehlen, Multibody Systems - Roots & Perspectives, Multibody Systems Dynamics, 2 (1997) 149188.
[4] R. Ryan, (2001). Functional Virtual Prototyping, MSC Software Publisher, Santa Anna.
[5] C. Alexandra, M. Commit, (2007). Virtual Prototyping of the Solar Tracking Systems, Proceedings of the International Conference on Renewable Energy and Power Quality - ICREPQ, Seville.
[6] S. Abdallah, S. Nijmeh, Two-Axes Sun Tracking with PLC Control, Energy Conversion and Management, 45 (2004) 1931-1939.
[7] M. Alata, M. A. Al-Nimr, Y. Qaroush, Developing a Multipurpose Sun Tracking System using Fuzzy Control, Energy Conversion and Management, 46 (2005) 1229-1245.
[8] K. Karimov, M. Saqib, P. Akhter, A Simple Tracking System, Solar Energy, 87 (2005) 49-59.
[9] S. Odeh, (2004). Design of a Single-Axis Tracking Collector, Proceedings of the 14th EuroSun Conference, Freiburg.
[10] P. Roth, A. Georgiev, H. Boudinov, Design and Construction of a System for Sun-Tracking, Renewable Energy, 29 (2004) 393-402.
[11] M. Commit, I. Vi§a, (2007). Design of the Linkages-type Tracking Mechanisms by using MBS Method, Proceedings of the 12th IFToMM World Congress, Besangon.
[12] I. Vi§a, D. Diaconescu, (2007). On the Incidence Angle Optimization of the Dual-Axis Solar Trackers, Proceedings of the 11th International Research Expert Conference - TMT, Hammamet.
[13] R. Sorichetti, O. Perpinan, (2007). Solar Tracking Systems Analysis, Proceedings of the 22nd European Photovoltaic Solar Energy Conference - EUPVSEC, Milano.