COMPUTATIONAL WELDING MECHANICS
Kinematic Models for Welding Heat Transfer
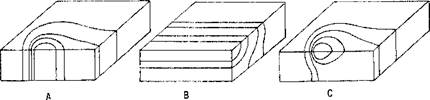
Having selected a model for the heat source, the analyst has the option of assuming that the heat flows only in cross-sectional planes, only in the plane of the plate, only in a radial direction or is free to flow in all three dimensions, Figure 2-12. Such assumptions are analogous to those applied to the displacement field in beams, plates and shells in structural analysis. Since assumptions restrict the orientation of the thermal gradient, it is suggested they be called kinematic models. Of course, these kinematic models are quite distinct from the heat source models described in the previous section. These three models are discussed in detail in [36].
|
Figure 2-12: By constraining the thermal flux and hence the temperature gradients, the kinematic models are consistent with the temperature fields shown in; (A) inplane, (B) cross-sectional models and (C) 3D models imply temperature. |
The most popular has been the cross-sectional model which assumes that heat flow in the direction of welding is zero. This is surprisingly a subtle model. Strictly, it is limited to steady state analysis of prismatic geometries with the weld parallel to the prismatic axis. How can such a model possibly be accurate since some heat clearly must flow in the direction of welding? The answer is that the heat input has been modified to account for the heat that flows in the longitudinal direction. Because it uses relatively few 2D elements, it is computationally one of the cheapest models.
The next most popular kinematic model has been the in-plane model. It assumes the heat flow normal to the weld plate is zero. The advantage of the in-plane over the cross-sectional model is its capability for computing the starting and ending transients. However, because it tends to require rather more elements and more time steps, the computational costs are higher [19]. It has not been used extensively.
In choosing a kinematic model, the analyst must balance accuracy against cost. In all cases, reality is three dimensional but the cost of analysis is the highest. Constraining heat flow to the plane of the plate can achieve useful accuracy for thin plates, particularly with deep penetration plasma, electron and laser beam welds. Assuming heat flows only in the cross-sectional plane can provide a useful and economical approximation for many welding situations. If the thermal diffusivity is sufficiently low and welding speed sufficiently high, this can be an accurate model. In particular, the results from a low cost cross-sectional analysis can be helpful in designing an efficient 3D mesh.
The thermal shell model is a generalization of the in-plane model to curved surfaces. It assumes that no heat flows normal to the surface and that all heat flows in the tangent plane, i. e., the temperature gradient lies in the tangent plane. Where conditions hold to an adequate accuracy, the shell model has several advantages. The shell element usually has half the number of degrees of freedom and half the bandwidth, which reduces the computing costs. Even more important, it allows larger elements than the equivalent 3D elements because they are better conditioned numerically.
In 3D analyses the kinematic model is obviously correct. The issue is to reduce the computational cost to acceptable levels for meshes that achieve useful accuracy. The principal tools are optimizing the mesh and creating efficient solvers.
In 3D analysis, brick elements are preferred because they tend to be more accurate and easier to use and interpret than tetrahedral elements. However, it is more difficult to grade a mesh with small brick elements near the welding arc to capture the rapid changes in temperature and with large brick elements far from the arc where the temperature varies slowly.
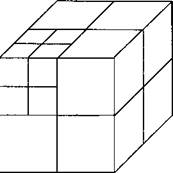
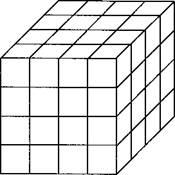
To solve these problems McDill et al. [10 and 47] developed a special brick element for graded 3D meshes. The grading elements of McDill have made a major contribution in optimizing the mesh for the analysis of welds. These elements reduce the computational complexity from О(n7) for a cube with uniform mesh with n elements on an edge to 0(log2 n) for the cube with a graded mesh. In both cases, the problem has a point load on one comer of the cube and direct solvers are used. In this problem, there is no accuracy loss with the graded mesh. The advantages of this element are demonstrated by analyzing the problem shown in Figure 2-13. In comparison the cost and the memory requirements vary as log2 n for the graded mesh. The larger the problem is the greater the advantage of the graded mesh. This clearly illustrates that the gains from better algorithms can easily outpace the gains from better computers.
|
|
|
|
|
I McDill’s grading scheme for a cube of equal to n3 and 7 log, n +1 . The n (Where: n is the number of elements the number of recursive subdivisions of of the element in the upper left front |
|
Figure 2-13: A uniform mesh n 4 (A) anc n=4 (B). The number of elements is computational cost varies as n7 and log2 along an edge in a uniform mesh and, m is the upper left hand cube. Note: the size comer is the same when n=2m). |
The second major weapon in the battle to reduce computing costs is the use of improved solvers. The use of incomplete Choleski conjugate gradient (ICCG) solvers with element-by-element preconditioning, which have been developed for fluids problems by Glowinski [12] and for structural problems by Jenning and Ajiz [13], has produced dramatic gains. These solvers do not factorize the global stiffness matrix completely.. Although the experience to date does not permit a definitive statement, Hughes [14 and 15] has developed an iterative method that promises to solve the problem and reduces CPU costs. The transient temperature fields shown in Figure 2-14 and 2-17 were computed on a workstation with such a solver.
The thinner the wall, the smaller is the three dimensional area around the heat source. An example is shown in Figure 2-14.
|
Figure 2-14: The contours of the transient temperature field are shown for a weld of a tee joint. The pipe is 40mm in diameter and the wall thickness is 2.5mm. Thermal shell elements are used to reduce the computing cost. The welding parameters are voltage 32, amperes 150, speed lmm/s and power input 1.5 kJ/mm. |
Since the 3D model is needed near the arc and the shell model is most efficient far from the arc, these models can be combined to produce a more efficient model. Figure 2-15 shows such a composite JD-shell model. It requires a special transition element to join shell and 3D brick elements.
|
real nodes nodes to be constrained bottom corner |
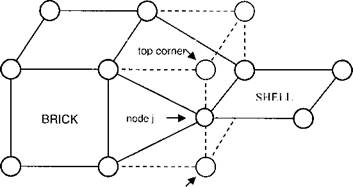
Figure 2-15: The transformation of a brick element to a transition element is shown. In particular, the relation between the transition node j and its top and bottom nodes is shown [67].
Gu in [67] presents a method to connect a three-dimensional element to the shell element. Figure 2-15 shows brick and shell elements and the transformation of a brick element to a transition element. The element is called a Shell-Brick transition element. It is not really a new element but a brick with constraints according to the shell assumption. It has more flexibility and can be added to other FEM packages without altering the original code.
|
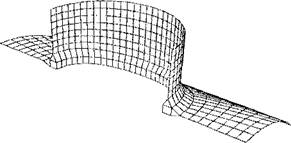
Figure 2-16: This tee joint is modeled with 4 noded thermal shell elements far from the weld joint, 8 noded 3D brick elements at the weld joint and special transition elements to join the shell and brick elements. |
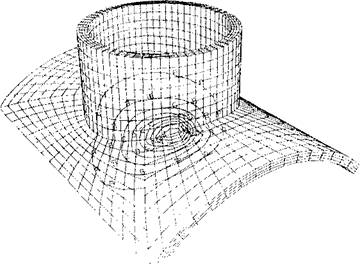
This composite kinematic model is more accurate than the shell mesh shown in Figure 2-16 and computationally cheaper than the mesh using 3D bricks shown in Figure 2-17.
|
Figure 2-17: This tee joint is modeled with 8 noded 3D brick elements. This is the most accurate and the most expensive kinematic model. |
The fundamental limitations of the most popular commercial mesh generators are that the mesh is difficult to change during an analysis; the mesh design requires expert judgment and it is labor intensive. Kela [7] and Sheperd and Law [8] developed a class of mesh generators which do not depend on expert judgment. They are fully automatic. Since as much as 90% of the time and cost of a Finite Element Method (FEM) analysis of a complex structure can be absorbed by pre and post processing, progress in mesh generation is a critical factor that is pacing the development of computational weld mechanics. Automatic mesh generators open the possibility of changing the mesh at any, even every, time step. This is particularly important in welding where a fine mesh is needed near the molten pool and a coarse mesh far from the molten pool could decrease costs and improve performance by several orders of magnitude. The arbitrary Euler-Lagrange method [9] would allow a fine mesh that moves with the arc. The mesh far from the arc could be stationary. The mesh in between could move with a velocity that is interpolated.
The above examples suggest that rapid improvements in mesh generation methods that will reduce the cost of finite element analysis (FEA) of welds and permit real welding situations to be analyzed routinely. Many manufacturing processes are threedimensional, nonlinear, transient processes in which the area of computational interest changes with time. Automatic finite element analysis AFEA with adaptive and dynamic mesh management has the potential to reduce substantially the cost of analysis for problems of this type.
In transient heat transfer analysis, the Finite Element Method (FEM) program must integrate a set of ordinary differential equations in time. Current commercial FEM programs use two point integration schemes that are either explicit or implicit. Explicit schemes use primarily element level operations. The cost per time step is small but time steps must be short because the element with the smallest critical time controls the time step. Implicit schemes solve a global set of linear equations. Each time step is more expensive but the time steps can be larger. Provided the load does not vary too rapidly in time, the longer time steps can be more efficient.
A recent development in integration schemes allows those elements with short critical time steps to be integrated implicitly with longer time steps and those elements with longer critical time steps to be integrated explicitly [17]. This can reduce computing costs significantly.
The generalization of this concept to use different time steps in different elements is called subcycling [16]. The mesh shown in Figure 2-18A is created by recursively subdividing the square m times.
|
В |
|
С |
|
A |
Figure 2-18: The mesh in (A) is obtained by recursively subdividing the square in the upper left hand comer. This can be significantly more efficient than the regular mesh shown in (B) or the grading strategy used in (C) for point like loads at the upper hand comer.
The number of elements is l+3m; the smallest element has edge length і/і"' and critical time step 22'"/a/.2 . If each element is integrated only with its critical time step, the number of element time steps is 3(2”' - l) or 0(2"'). If all elements are integrated with the smallest critical time step as is the current commercial practice, the number of element time steps is: ( + 3m)22n' a/L2 orO(m22m).