COMPUTATIONAL WELDING MECHANICS
Boundary Conditions
On the boundary of the domain Q either the essential (prescribed temperature) or natural (prescribed flux) boundary conditions must be satisfied. The essential boundary condition can be defined as: T(x, y,z, t) T|(x, y,z, t) on the boundary Sj, i. e., (x, y,z)^ S]. t ^ 0 (3-16)
The natural boundary condition can be defined as:
Kn— + q + h{T-Ta)+ae(T*-T*)=0 (3-17)
on
On the boundary S2: i. e. (x, y,z) є S2: t > 0 кп - thermal conductivity normal to the surface (W/mC) q(x, y,z, t) = a prescribed flux (W/m2)
h = heat transfer coefficient for convection (W/m2С)
a = Stefan-Boltzmann constant (W/m2C4)
e = emissivity
To = the ambient temperature for convection and/or radiation
If radiation is included or if the convective heat transfer coefficient is temperature dependent this boundary condition is nonlinear.
In addition, the initial condition must be specified for (x, y,z) є D. : T(x, y, z,0) = To (x, y,z) (3-18)
If the partial differential equation (3-1), the boundary conditions (3-16) and (3-17), and the initial condition (3-18) are consistent, the problem is well posed and a unique solution exists.
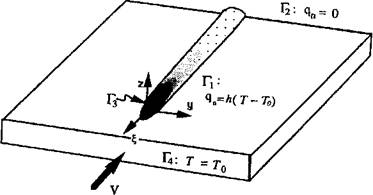
The most convenient domains in which to apply equations (3-7) are prisms with constant cross-sections, as found in the example shown in Figure 3-6. The temperature of the boundary between the weld pool and the solid is prescribed to the solidus temperature. By using an essential boundary condition, Gu et. al. [2 and 14], the heat entering the base metal through the interface,/^, equals the thermal reactions, and the flux due to complex radiation and convection on the surface of the weld pool need not be taken into account.
|
Figure 3-6: The Eulerian frame and boundary conditions. Г2 is the downstream boundary that is normal to the velocity of the source. On this surface the gradient of the temperature has been prescribed to zero. Г3 is the surface of the liquid- solid interface of the weld pool. On this surface, which is smooth but with arbitrary orientation and curvature, the temperature has been prescribed. Г4 is the surface of the upstream end. The outward normal of the surface is parallel to the velocity of the source. On this surface the ambient temperature of the plate has been prescribed. Г] is the remainder of the boundary surface. The outward normal of the surface is orthogonal to the velocity of the source. On this surface natural convection has been applied. |
From experimental measurements, we know that at a sufficient distance, in front of the weld pool, temperatures remain at ambient temperature; T=Tq when £ ><f„ and consequently, <p=0 when £>£„.
When the prism boundaries as /} are not insulated, a boundary flux would have to be applied. For the case of a constant convective coefficient, h, the boundary conditions is:
qn=-kWT-nr=h(T-T{;) (3-19)
where qn is the scalar external flux and «г is the outward normal vector on the boundary.
We express equation (3-19) in terms of ф, using equation (3-6):
f /ТЛ,
|
іЯТ-пт = ке |
V(p-nr~—щ }=-Ье~Ы)/2(р (3-20)
2
On the side walls of the prism, nr is orthogonal to the weld path,
|
(3-21) |
Equation (3-20) for the side walls becomes:
Y7 h
|
(3-22) |
V(p-nr=--(p
The heat source term has been set to zero. If one wished to include the weld pool, a heat source term exists that could replace the prescribed temperature boundary condition on the weld pool solid-liquid interface.
If the domain is long enough or infinite, at the downstream end the temperature will drop to ambient temperature because of the heat dissipation from the surfaces. Either essential or natural boundary conditions can be applied, i. e., T-To or V7’ nr=0when ^=>-oo. Transforming temperature T to the potential function ф, when Vr-nr = 0 is applied and ^=>-oo,
|
(3-23) |
УТ-пт=е~(^)І2 У(р-пг-™(рпА= 0
|
|
So,
(3-24)