ЧТО МОЖЕТ ВИБРАЦИЯ?

Гироскоп на вибрирующем основании

Вибра­ция основания гироскопа при наличии упругой податли­вости элементов подвеса может привести к весьма неже­лательному явлению — отклонению осп гироскопа от за­данного направления. Рассмотрим этот эффект в качест­ве еще одного примера простого подхода к вычислению вибрационного момента.

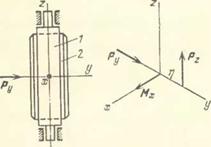
Пусть xyz — прямоугольная система координат, свя­занная с внешним кольцом 1 подвеса гироскопа (рис. 2.5, а, б), причем ось z направлена по оси кольца, ось х — по оси поворота кожуха 2, в который заключед ротор гироскопа. Пусть, далее, вибрация основания тако­ва, что при абсолютной жесткости подвеса его геометри­ческий центр, совпадающий с центром масс ротора гиро-
скопа, совершает прямолннейпые гармонические колеба­ния по закону

х = a cos at, у — b cos at, z = с cos at, (2.33)

где а, b и с — амплитуды составляющих вибрации по со­ответствующим осям координат. Тогда возникает сила

инерции в переносном движении, проекции которой на оси координат

Рх = —тх = та a2 cos at,

Р„ = —ті/ = mba2 cos at,

Pz = —mi = mca2 cos at. '

Предположим теперь, что подвес линейно податлив в направлении оси у, причем коэффициент жесткости ра­вен с0. Тогда под действием силы Р„ центр масс ротора будет совершать колебания, описываемые хорошо извест­ным дифференциальным уравнением (силами сопротив­ления пренебрегаем)

тт + с0т] = mba2 cos at.

Решение этого уравнения, соответствующее вынужден­ным колебаниям, имеет вид

Л = 7ZT^^osat (2.34)

3 Ц. II. Блехман 33

Но при перемещении центра масс ротора по закону

(2.34) возникает момент от составляющей силы инерции Р2 (см. рис. 2.5, б), ось которого направлена по оси х:

4

Мх = гРг — тЪс —2 COS2 at,

р — со

Среднее за период Т = 2л/со значепие отого момента как раз и будет представлять собой вибрационный момент

Vx = <МХ) = - І - гпЪс (2.35)

z р — со

Поэтому, как следует из известного положения механи­

ки твердого тела, возникает прецессия гироскопа вокруг вертикальной оси z со средней угловой скоростью

.. _Vx mbc со3 /0 осч

^ = 7^= 277^* <2'36)

где J — момент инерции ротора относительно осн у.

Из формулы (2.36) следует, что при р > со направле­ние прецессии противоположно тому, которое имеет ме­сто при р < со; этот интересный качественный результат

подтверждается экспериментом.

2А. Общий способ получения основного уравнения вибрационной механики и выражений для вибрационных сил (метод прямого разделения движении)

Остановимся теперь несколько подробнее па рассуждениях и выкладках, приводящих к уравнению (2.3) и к выяспению весь­ма важного вопроса о способах нахождения вибрационной силы V.

Как и выше, пусть движение системы описывается дифферсп - циальпым уравнением (2.1) и оно представимо в виде суммы мед­ленной составляющей X(t) и быстрой составляющей |)(<, ш() согласно равепству (2.2). Будем для упрощения изложения счи­тать быструю силу Ф(і, х, t, сof) периодической по быстрому вре­мени т = сог, а )’(г, со/) — периодической функцией т с тем же периодом 2я. Положим также для определенности представле­ния (2.2), что среднее за период 2л по т = со< значение функ­ции г|? равно пулю:

<|>(<, со<)> = 0. (2.37)

Здесь угловые скобки означают усреднение за период 2л по быстрому времепп т = cot, входящему как лвпо, так и через посредство функции г)>. Заметим, что при выполнении условия

А(<) = (x(t, со«)>,

т. е. медленная составляющая X является соответствующим сред­ним значением координаты х.

Подставим выражение (2.2) в уравнение (2.1) и, пользуясь имеющимся произволом (вместо одной неизвестной функции х введены две — X и ф), потребуем выполнения соотношения

тХ = (F(X - j - if, X + і)-, г)) + <Ф (А' + ]з, X + г|з, г, ш) >, (2.39)

представляющего собой результат усреднения исходного уравне­ния. Тогда должно выполняться также уравнение

щур = F(X -f-i|i, А' + [), ;) — (F(X + ф. А + t)) +

+ Ф(Х - f - ф. А + i|), t, соt) — <Ф(А + if. А + |5, t, сої)). (2.40)

Мы получили вместо дпффорепциалытого ураппепия (2.1) си­стему двух интегродифференциальпых уравнении (2.39), (2.40), причем пока еще не было использовано никаких предположений о темпах измепеппя функций А и |

Допустим, что найдено решение А п ф уравпений (2.39) и

(2.40) . Тогда, подставив г|з в уравнение (2.39), как раз и получим уравнепие вида (2.3)

mX = F(A, A, t) + У (А, А, /), причем вибрационная сила V определяется выражением

Иными словами, уравнение вибрациопной механики (2.3), в сущ­ности, справедливо при весьма общих предположениях.

Согласно (2.42) вибрационная сила V представляет собой ре­зультат усреднения по быстрому времени «собственно быстрой силы» Ф и того быстрого вклада Fь который выделяется из мед­ленной силы F на траектории движения системы * = А + ф. В со­ответствии с этим можно различать собственно вибрационную си­лу = <ф> и индуцированную вибрационную силу У(і) = (F,). Наличие этой последней составляющей приводит к тому, что бы­стрые движения в нелинейной системе могут возиикиуть и при отсутствии быстрых сил Ф в исходном уравнении. Специфика это­го «автономного по быстрому времени» (или автономного в обыч - пом смысле) случая состоит в том, что уравнение (2.40) непре­менно допускает тривиальное решение = 0; интерес же пред­ставляют быстрые «автоколебательные» периодические решения для 1|э, период которых заранее неизвестен и должен быть пай - ден в процессе решения задачи; медлепная сила F для сущест­вования таких решений должна быть пелипейной по х или £.

Обращаясь теперь к вопросу о решении системы уравнений (2.39), (2.40), заметим, что в общем случае оно не проще, чем решение исходного уравнения (2.1). Однако если учесть основное

предположение о темпах изменения функции X и ф, то представ­ляется естественным следующий прием приближенного решения этой системы. Вначале решается уравнение (2.40), прпчем вели-

чпиы X, X и t, пзмепепие которых за период быстрого движепия 2я/ш относительно мало, в процессе решения считаются постоян­ными («замороженными»). Предположим, что при этом уравне­ние (2.40) действительно допускает периодическое по сof решение

1)з = і): (X, X, f, соt) и что это решение найдено. Тогда можно бу­дет найти выражение (2.42) для вибрационной силы V и соста­вить уравпение (2.41) для медленной компоненты движения X; естественно, одпако, что теперь это уравнение («уравнение вибра­ционной механики») будет лишь приближенпым.

Уравнение (2.41) обычно значительно проще исходного урав­нения (2.1); в частности, как будет показано (см., например, раз­дел 12). в случае системы с несколькими степенями свободы уравпепия медленпых движений, соответствующие уравнению

(2.41) , имеют значптельпо меньшую размерность. Вместе с тем, как отмечалось, это уравпение содержит информацию, достаточ­ную для объяснения и описания большинства интересующих нас эффектов.

Обоснование изложенного приближенного приема получения уравнения (2.41) в духе асимптотических методов нелинейной ме­ханики, а также его более подробное изложение можно найти в работе [40] [8]); не останавливаясь па приводимом там доказатель­стве, отметим, что достаточные условия применимости этого прие­ма сводятся к двум основным требованиям: 1) периодическое ре­шение i|)(.Y, A', t, сог) уравнения быстрых движений при «заморо­женных» X, X и ( должно быть асимптотически устойчивым по

со< при всех X, X и t из рассматриваемой области; 2) если X и if одного порядка, а порядок правой части уравнения (2.39) при­нять за пулевой, то правая часть уравнения (2.40) должпа иметь порядок 1/е2, где е = 1/со — малый параметр; последнее тре­бование представляет собой формализацию указанного выше пред­положения о темпах изменения функций X и 1|),

Поскольку функция т|) входит в выражепие для V под знаком интеграла, то часто можно ограничиться приближенным опреде­лением функции г|з из уравнения (2.40), например в виде суммы небольшого числа гармоник или членов ряда по степеням малого параметра.

Часто можно считать, что г|> мало по сравнению с X (X мало •

по сравнепию с і)) в силу исходного предположения). Накопец, во многих важных случаях можно считать, что быстрая сила Ф зна­чительно больше медленпой силы F, и пе учитывать эту силу при решении уравнения (2.40) (см. п. 2.3). В таких случаях будем говорить о чисто инерционном приблиокении при решении урав­нений быстрого движепия. Как нетрудпо видеть, в этих случаях,

а также когда в разложении фупкции F по і|з и |з вблизи - ф = 0 п ф = О учитываются лить лппепные слагаемые, ипдуцпроваппая вибрационная сила отсутствует (У(і> = 0) и У = У(8) = <Ф>.

Из приведенных соотношений видно, что ошибки не произой­дет, если некоторые илн все медленные силы отпести к быстрым; именно так следует поступать в сомнительных случаях. Отметим также, что изложенное легко распространяется па случай урав­нений с почти периодическими по cot правыми частями, а также на случай, когда при Г-периодической силе Ф уравнение (2.40) до­пускает решения периода Tplq, где р и q — целые положитель­ные числа.

Отметим также, что, составив уравпение (2.41), мы можем осуществить апостериорную проверку исходного допущения о раз­делимости движений, т. е. убедиться, что решения этого уравне­ния действительно медленные по сравпепию с решениями уравне­ния (2.40). Так, в случае когда уравнепие (2.41) или соответст­вующее ему уравпение в вариациях оказываются линейными с постоянными коэффициентами, требовапие разделимости движе­ний сводится к условию

h < со (і = 1.................... п),

где — существенные частоты колебаний системы, описываемой этими уравнениями (эти частоты, естественно, сами могут зави­сеть от частоты со).