Асинхронные электроприводы с векторным управлением
Принцип ориентации вектора тока по вектору потокосцепления асинхронного двигателя
Метод управления частотными электроприводами, получивший название метода векторного управления, разрабатывался в конце 70-х и начале 80-х годов [I, 22, 23].
В настоящее время наиболее распространенными системами векторного управления являются системы, использующие в качестве опорного вектора векторы главного потокосцепления машины или потокосцепления ротора.
Электромагнитный момент машины переменного тока
- f ”L-lm ('Л - т"Im ('А) - fp тг, m t'A). <u>
где m — число фаз машины; р — число пар полюсов; Lm — взаимная индуктивность обмотки статора и ротора (индуктивность намагничивающего контура); Lr — собственная индуктивность обмотки ротора; Is— вектор тока статора; Фо— вектор главного потокосцепления; Wr — вектор потокосцепления ротора; Im — операция взятия мнимой части комплексного числа; звездочкой обозначена операция комплексного сопряжения.
Во всех случаях Im (XY*) = | X || Y | sin (УТ), где угол между векторами отсчитывается от второго вектора к первому (Y X). Это соотношение может быть представлено в виде YX2, где
Х% = | X | sin {YX) — проекция вектора на ось ординат системы координат, связанной с вектором Y. Отсюда электромагнитный момент машины переменного тока
= <‘-2)
где /s2 — проекция вектора тока статора на оси ординат систем координат с опорными векторами 1Г, 4V
Заметим, что три вектора являются попарно-независимыми, так как каждый из них выражается через два других:
VTf гг хт г L>m
|
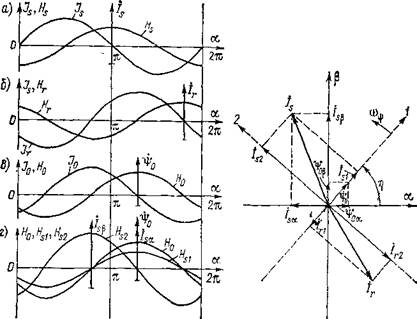
1.1. Распределение и изображающие иек - 1.2. Векторная диаграмма обоб - торы электромагнитных переменных щенных векторов 'Ро и It асинхронной машины |
Наглядную интерпретацию соотнешений (1.1) и (1.2) можно дать, рассмотрев пространственное распределение плотностей тока по расточке статора и ротора машины, а также распределение напряженностей магнитного поля в зазоре машины при раздельном и совместном их действии. На рис. 1.1 представлены плотности тока и напряженности магнитного поля и изображающие векторы. При таком представлении всякий комплексный вектор есть вектор, связанный с системой координат с началом на оси вращения машины, вещественная ось которой отождествляется с осью абсцисс, а мнимая — с осью ординат, модуль вектора — с мгновенной амплитудой соответствующей электромагнитной переменной. На рис. 1.1 представлено разложение синусоидального распределения напряженности магнитного поля от тока статора на два распределения в системе координат, ось абсцисс которой связана с распределением напряженности магнитного поля в зазоре машины. В соответствии с этим разложением имеет место разложение и обобщенного вектора тока статора в указанной системе координат.
Здесь необходимо сделать весьма важное замечание: отображение распределений напряженности магнитного поля и других электромагнитных переменных вектором возможно только при наличии обмоток или геометрической форме зазора,
обеспечивающих синусоидальные распределения. Сказанное позволяет интерпретировать машину переменного тока как эквивалентную машину постоянного тока.
Сопоставим ротор асинхронной машины с якорем машины постоянного тока, а статорную обмотку — с обмотками возбуждения машины постоянного тока. Тогда составляющая тока статора, синфазная главному потокосцеплению, может интерпретироваться как ток возбуждения машины постоянного тока, составляющая тока статора, сдвинутая на угол л/2,— как ток компенсационной обмотки, составляющая тока ротора, сдвинутая на угол л/2 относительно — как поперечная составляющая поля якоря, и составляющая, синфазная главному потокосцеплению,— как размагничивающая продольная реакция якоря. Все векторные соотношения представлены на рис. 1.2. На диаграммах видно, что главное потокосцепление То есть векторная сумма тока статора ls и тока ротора I, и, следовательно, в системе координат, связанной с вектором главного потоко - сцепления, составляющие векторов ls и I, на ось ординат 2 равны и имеют разные знаки Is2 = —Ira, а составляющие hi и Iri определяют модуль главного потокосцепления |Фо| — = Lm(Isi+ Iri); там же видно, что составляющая 1, является размагничивающей.
Основными особенностями, отличающими описанную интерпретацию асинх-ронной машины от машины постоянного тока, являются:
а) отдельно эквивалентной обмотки возбуждения и компенсации поперечной реакции якоря на статоре асинхронной машины нет, эти обмотки как бы совмещены;
б) ось, связанная с главным потокосцеплением (/), вращается относительно статора; оси 1 и 2 вращаются относительно неподвижной системы координат (а, р).
Эти особенности векторного формирования момента машины диктуют главные задачи, подлежащие решению 'при аппаратурной реализации системы векторного управления. Первой задачей является измерение вектора главного потокосцепления. Решение ее следует из представления вектора в виде
1Po==l'irol(cosTi-b/sinTi), (1.4)
угол rj является углом (электрическим), отсчитываемым от оси а (магнитная ось фазы А) до соответствующего мгновенному значению положения вектора главного потокосцепления, или, учитывая интерпретацию этого вектора как вектора, связанного с волной напряженности магнитного поля, до максимума напряженности магнитного поля в зазоре. Угол г] измерить затруднительно, но можно получить составляющие Тоа = = 14^01 cos т] и ¥0р = 1 Ф'о 1 sin т), установив, например, датчики Холла на ось а и на ось р, сдвинутую на угол я/(2р) в рас* точке статора. Получить оценки Ч^оа и Tog можно и на основе
измерения других электромагнитных переменных, о чем будет сказано ниже.
На рис. 1.2 приведены разложения вектора /5 по осям (а, р) и (1, 2). Составляющие вектора /* в системе координат (а, |3) :
Isa = h-jVB + IcY, /,р = ^(/В-/С), (1.6)
где 1д, 1в, 1с — мгновенные токи фаз статора.
В систему координат (1,2) проекции вектора тока lsa, /4р пересчитываются с помощью уравнений:
4l = ha cos n + /sfJ Sin rj; Is2 = — lsa sin 11 + /s|5 COS 1).
Заметим, что проекции вектора тока статора в системе координат (1,2) представляются сигналами постоянного тока и не зависят от частоты питания машины. Учитывая интерпретацию составляющих тока статора, система управления может строиться аналогично системам управления машинами постоянного тока — управления моментной составляющей тока статора /s2 с целью формирования электромагнитного момента машины и квадратурной составляющей тока lsь определяющей модуль главного потокосцепления [см. выражение (1.2)], и управления модулем главного потокосцепления.
Аналогичная интерпретация векторного управления приведена в работе [1].