Асинхронные электроприводы с векторным управлением
Контур регулирования модуля вектора потокосцепления ротора двигателя и особенности его настройки
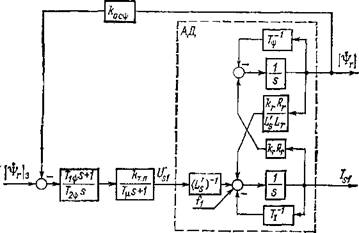
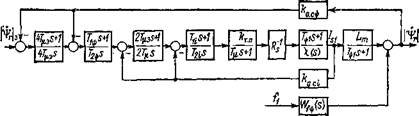
На рис. 3.2 представлена структурная схема асинхронного двигателя с контурами регулирования переменных | V,. |, /s) и контуром управления UsX перекрестная связь L'co^,r/s2 яв-
|
і 2. Структурная схема контура регулирования модуля потокосцепления ротора |
|
■ іется возмущением, не зависящим от переменных рассматри- іемого канала. Дифференциальные уравнения, описывающие ■ анал управления модулем потокосцепления ротора, имеют вид: rfl^rl Rr |
|
гі + МЛ; krRr ■ 1 -ії-Чг + - р-ил + и. |
|
Lr |
|
dt Rs + kX |
|
(3.6) |
|
£si dt |
|
Уравнения относительно переменных и hi линейны, по тому можно применить преобразование Лапласа. Характеристическое уравнение имеет вид |
|
A(s) |
|
(3.7) |
|
Корни этого уравнения о— 1 ( Я» . Rr Гі, А . A[RsRrKLsLr) 1. 2tr Ls Lr ) L У {RslLs + Rr/Lr)2 J ’ 1 ( Rs і Rr ^ Г1 _J_ л. і rr ^ IRs^r/i^s^r)] "I - 20 I Ls + Lr ) L1 + V (Rs! Ls + Rr/Lr)2 J • |
|
«2 |
|
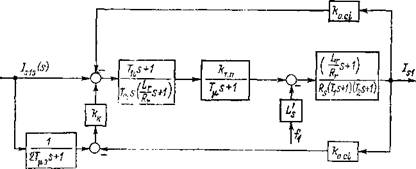
Корни различаются по значению, и s2 > «і. Структурная схема контура регулирования тока hi приведена на рис. 3.3. Для контура управления составляющей тока татора hi (s) в знаменателе передаточной функции имеется ;дин существенный корень si, а сама передаточная функция шеет вид |
|
(s + Rr/Lr)/Lt A (s) |
|
ш- |
|
Usі (s). |
|
(3.8) |
|
Ж») |
|
ys) |
|
(T, S+1)(T2S+1) |
|
ws) |
|
1 |
T1ts-H |
^Т. П |
|||
|
Тіі* |
TpS+1 |
*"V |
|
’ас. т |
3.3. Структурная схема контура регулирования составляющей тока Is
Корень Si близок по значению к Rr/L,. Передаточная функция для модуля потокосцепления ротора относительно составляющей Is 1 (s)
krRr
|
(3.9) |
S + Rr/Lr
или при входном управляющем сигнале Usi{s)
|
(3.10) |
I *rl(s) = -^rtf, l(s).
На основании соотношения (3.10) и при условии Si < s2 можно сделать вывод, что канал управления модулем потокосцепления ротора достаточно выполнить одноконтурным (рис. 3.2). Однако влияние канала управления угловой скоростью в модуле потокосцепления ротора будет
(3.11)
При замыкании контура управления модулем потокосцепления ротора при помощи ПИ-регулятора с настройками Wp(s) = T^s + 1 Тр9 = Гц + Г2; Т^ = Т, — Sj Т^ =
К. п^т^о. с it)
= 27’,
Иэ Rs
По управляющему сигналу получим
|
у - 1 ко. сф |
|
l'Frla(s); |
|
(3.12) |
|
2 ТІ/ + 2 T^s + 1 |
|
l*,l(s) = |
возмущение от перекрестной связи
|
h(s). (3.13) |
(У/Л)МУ + 1)
6|Wr|(s)
|
61^1(5) |
|
■ш. (3.14) |
|
(2r2ss2 + 2V+l)(r2s+l) |
При использовании в системе прямой компенсации выражение для возмущения от перекрестной связи будет
|
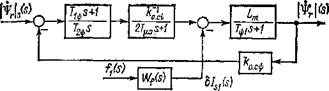
8.4. Структурная схема внешнего контура управления модулем потокосцепления ротора |
Контур управления составляющей тока статора Isі (рис. 3.3) содержит ПИ-регулятор с фильтром, и его уравнение по управляющему сигналу /«и (s)
k~l
|
(3.15) |
R0. С I
|
hi (s) ■■ |
hl3 (^)l
2Г*/ +27^+1
ГД0 T21 2T|_4э^т. п^о. с //
по возмущению от перекрестной СВЯЗИ f(s)
м (-л {2ТМ/*Л(Ч*г)> + l](V+l)rf,(s)
S1 (zwv3+2 V+2 v+0 (ri*+о ‘
При определении передаточной функции по управляющему сигналу полиномы, соответствующие малым постоянным времени Гр, и Т2, были заменены полиномом первой степени с постоянной времени, равной Т^, а при вычислении передаточной функции по возмущению учитывались оба полинома.
При использовании прямой компенсации воамущение от перекрестной связи
&hi(s) = X
X [(27;э7у>3 + 27>2 + 2T^s + 1) (7> + I)]"1. (8.1?)
Уравнение контура управления | | (s) (рис. 3.4) по управ
ляющему сигналу
|
(3.18) |
^0. с-ф
M'^ + v +1
по возмущению, без прямой компенсации,
|
6|ФлКФ |
|
(3.19) |
(вГ®^ + 8Т%/ + 4T^s + 1) (7> + f j
|
ЛS) |
|
Rs |
|
(3.20) |
|
с использованием прямой компенсации L'„ |
|
(8Г^/ + 8Г2/ + 4Г^+1)(Г15+1) ' |
|
от2 'г с3/ 01 }ЛЗІ |Д,* |
В контуре управления модулем потокосцепления применен ПИ-регулятор:
(s) = (Т+ l)/(r2lts); Г1ф = Lr/Rr
Г2
Полином передаточных функций по возмущению /4(s) = = 2Т»ъТ2Т^3 + 2Гдэя2 + 2Г, х^ + 1 заменен полиномом Л (s) « ~27ts2 + 27V3s+ 1.
Максимум коэффициента усиления по возмущению соответствует частоте Q0 = 1/(2Гр, э), при этом нормированная передаточная функция имеет вид:
|
— |
|
л. |
|
(3.21) |
|
(р + 1) (р2 + р + 1) (-27^- Р + l) |
|
GO |
|
м-э |
Ослабление возмущения определяется выражением
і к і (^т^цУ^^цэ) (2^цэ) . /п пп
Атах уз {1 + [Гі/(2 W}«,5 '
при Тх ~ 0,5 (Ls/Rs + Lr/Rr) получим
ltfmaxl<7V/(V2 7V9).
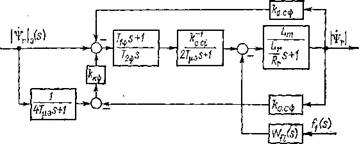
Подавление возмущения от перекрестной связи при помощи контура с эталонной моделью в технической реализации оказывается проще. На рис. 3.5 приведена структурная схема контура регулирования тока hi с эталонной моделью. Уравнение
|
З. Б. Структурная схема контура регулирования тока /S1 с эталонной моделью |
|
для этого тока по управляющему сигналу /,1 (s) = [kZ‘с / (27W(*K +1)5+1) /,|, (s)] х X {[ЩЛК + 1)52 + +1)^ + 1] (2V + or’- <3-23> Из соотЕЮшения (3.23) видно, что на частотах со < 1/(27^) и kK>5 фазовая характеристика для передаточной функции WIsX (s) мало отличается от нуля и передаточная функция не отличается от модельной: W uis{s)=I S{s)j I s3{s)=kZ^i{2T. Возмущение от перекрестной связи будет 1 |
|
(■^7s + 1)(V+1)27’i1Xf (») |
|
(6к+ »)/?» ( 27* |
|
(3.24) |
|
6/51(ф |
|
о |
|
2 т, |
|
цэ |
|
s+ 1 1(Г,5+ 1) |
|
s2 + |
|
Контур управления модулем потокосцепления ротора |'Ф’гI может быть также снабжен дополнительным контуром с эталонной моделью (рис. 3.6). Возмущение || (5) при примене- . нии эталонной модели 6l^l(s>~[(V+'~)k+4 «У PV+ ‘)Х X (3> + 1) Ms)] [(7> + 1) ( 2Г"1*+ [> + l)x |
|
)Г |
|
4T^s (27^ + 1) |
|
( |
|
+1 |
|
(3.25) |
|
X |
|
k, 4- 1 кф |
Использование контуров с эталонной моделью уменьшает усиление возмущения в [(feK + 1)(6К1|,+ 1)] раз и максимальный коэффициент усиления сдвигается в область частот, больших У(*к+ 1)/2/Т„ и V(*+ 1)/4/^э, где могут быть резонансы. Однако точный учет всех малых постоянных времени (Т2 и Гр,) показывает, что столь высокие частоты системой не пропускаются (1 < kK < 3).
|
3.6. Контур управления модулем иотокоецеилеиия [WrJ с эталонной моделью |
|
3.7. Структурная схема контура регулирования модуля потокосцепления с цепочечным регулятором |
Управление модулем потокосцепления ротора может быть также выполнено с контурами цепочечного типа. Структурная схема такого контура приведена на рис. 3.7. По управляющему сигналу уравнение для выходной переменной будет
*°:k(2V+‘) '...М;
|
/,,м по возмущению |
(3.26
4Туз+(2Т^з+)2
|
blsl(s) |
|
(3.27) |
К/ (i£-8 + О (V +1) жf,(s)
(2^э V2*3 + 2 V + 2^3* + 0 (2^3* + 1) (V + 1)
При выводе выражения (3.27) использованы упрощения, аналогичные упрощениям при выводе (3.16). Подавление возмущения получается несколько хуже, чем при использовании прямой компенсации. Замыкание контура управления потокосцеп - лением I’Frl определяет возмущение в модуле потокосцепления ротора;
бі I г 1 (S) = { {1671U3 UtUs3 + (27V+ I)2]} X X (16 V + 167^3 + ШГ2/ - f 67^5 + l)-lX
X [(V + l) PM/*.] l(2T»W+2 V+2 V + О X
|
(3.28) |
X (27>+!)(?>+1)] 1 > A (s).
Используя обычные замены полиномов при аппроксимации модулей частотных характеристик, получим:
| (4Г»/ + 4 V + iTms + 1) | ~ | {1Tns + I)«|, |(27'„/,lV + 2r;,S>-l-2V+ 1)|~|(2ГЮ*+ 1)|. (3'29)
В полосе частот са < 1/(47’(1Э), а также при | (T^s + 1) | 1
получим
6t | Wr I (s) ~ - ■ 16Г£/(*)--------------
(8Г^ + 4Ги» + 1)(2Гив+1)(Г1*+1)
На частоте 1/(27’м, э) получим значение модуля {[7’i/(27’p,3)]2 + + I}-0'5, так как Т{ примерно на порядок больше 2Г^. Замыкание контура | | определяет полное возмущение
61 Wr | (s) = —і—^—j—167ms! S*s(Wl*)M <s>----------------------------------- _------ (331)
(8ТІ/ + 4T^s + 1) (47^5 + 1) (27-^s + 1) (7> + 1)