Solar energy in progress and future research trends
Non-linear models. modification of the Angstrom equation with two six-month seasons, namely, October-March and April-September periods leading to two different linear models as
^ = 0.18 + 0.60 S (37)
H0 S0
and
H S
— = 0.24 + 0.53 — (38)
H0 S0
respectively. It is to be noticed that although the summations of (a + b) in these two models are the same, but a and b values have different distributions in two seasons. In some way use of these two linear models is dividing the overall linear variation domain between H/Hq and S/Sq into two nonparallel linear estimation models.
Gopinathan [47] has related the Angstrom parameters, a and b, to geographical elevation, h, and the ratio of sunshine duration as follows
a = 0.265 + 0.07h - 0.135 — (39)
S0
and
b = 0.265 - 0.07h - 0.325— (40)
|
a = 0.395 - 1.247 + 2.680 S0 S0 |
![Подпись: Different versions of Angstrom linear models are in use extensively in the solar energy studies for estimation of the global terrestrial solar irradiation amounts from the sunshine duration data. However, atmospheric turbidity and trans-missivity, planetary boundary layer turbulence, cloud thickness temporal and spatial variations cause embedding of nonlinear elements in the solar radiation phenomena. Hence, the use of simple linear models cannot be justified physically except statistically without pondering to obtain the model parameter estimations. In the literature, most often the Angstrom equation is either modified with the addition of extra terms with the hope to explain the nonlinear features or adjustment of the linear model parameters by relating them to geographical, meteorological and other model parameters. Most of the sunshine based solar irradiation estimation nonlinear models are modifications of the Angstrom expression in Eq. (36). Some authors have suggested change of the model parameters, a and b, seasonally, for arriving at better estimations. Different authors have expressed the global irradiation in terms of the sunshine duration and the geographical location [1,11,104,119,136]. Hay [54], on the other hand, related clouds and the atmospheric conditions to the solar irradiation estimation. He proposed the use of Eq. (36) with a modified day-length instead of S and solar irradiation that first hits the ground instead of H. In search for the nonlinearity effects, it is suggested to make](/img/1125/image042.gif) |
 |
S0
![]()
![]() and
and
b = 0.395 + 1.384 - 3.248
S0 S0
After the substitution of these parameters into the basic Eq. (36), the Zabara model for Greece appears as in Fig. 17.
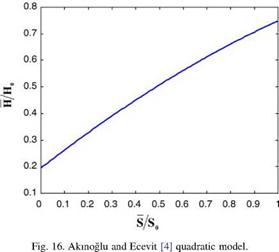
Akinoglu and Ecevit [4] found a global relationship between the Angstrom parameters by using the published a and b values for 100 locations from all over the world and the relationship is suggested in the following quadratic form
2
Given b this expression provides value of a and its substitution into Eq. (40) leads to a nonlinear model.