СВЕДЕНИЯ О РАСЧЕТЕ МНОГОЭТАЖНЫХ КАРКАСНЫХ И ПАНЕЛЬНЫХ ЗДАНИИ НА ГОРИЗОНТАЛЬНЫЕ НАГРУЗКИ
Расчетные схемы многоэтажных каркасных и панельных зданий устанавливают в зависимости от их конструктивных схем и способа восприятия горизонтальных нагрузок — по рамной, рамно-связевой или связевой системе. Междуэтажные перекрытия рассматривают как жесткие, не деформирующиеся при изгибе в своей плоскости горизонтальные связевые диафрагмы. Об учете в необходимых случаях влияния изгиба перекрытий в своей плоскости см. далее в п. 9.
Расчетные схемы рамно-связевых систем отражают совместную работу многоэтажных рам и различных вертикальных диафрагм: сплошных, комбинированных и с проемами (рис. XV.31). Вертикальные конструкции, в действительности расположенные в здании параллельно друг другу, изображаются стоящими рядом в одной плоскости и соединенными стержнями-связями, поскольку горизонтальные перемещения их в каждом уровне равны. Роль стержней-связей между многоэтажной рамой и вертикальной диафрагмой выполняют междуэтажные перекрытия. Эти стержни-связи считаются несжимаемыми и нерастяжимыми. Жесткость вертикальной диафрагмы в расчетной схеме также принимают равной суммарной жесткости соответствующих вертикальных диафрагм блока здания.
Расчетные схемы связевых систем отражают совместную работу вертикальных диафрагм многоэтажных каркасных или панельных зданий в различных сочета
ниях: сплошных и с проемами, с одним и несколькими рядами проемов (рис. XV.32). В этих расчетных схемах вертикальные диафрагмы, в действительности расположенные в здании параллельно друг другу, изображаются стоящими рядом в одной плоскости и соединенными стержнямр-связями.
А) 6) 6)
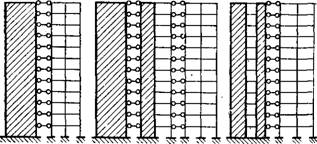
Рис. XV.31. Расчетные схемы рамио-связевых систем с диафрагмами а —сплошной; б —сплошной и комбинированной; в —с проемами
В) 6) в)
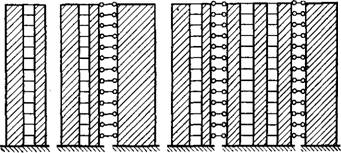
Рис. XV.32. Расчетные схемы связевых систем с диафрагмами а — с проемами; б — с проемами и сплошными; в — разнотипными
ВлйяШем продольных деформаций ригелей, перемычек и стержней-связей между вертикальными конструкциями ввиду малости значений пренебрегают. Также пренебрегают деформацией сдвига стоек рам и вертикальных диафрагм. Отношение высоты сечения вертикальной диафрагмы к ее длине обычно составляет
|§.v Влияние податливости стыков стоек и ригелей учи - ІІнвают в расчетах соответствующим снижением их по - рЮТнбй жесткости. Влияние же податливости стыков вертикальных диафрагм, как показали исследования, мо - ІЗкет учитываться в расчетах снижением их изгибной мкесткости примерно на 30 %.
* В расчетных схемах многоэтажных зданий регулярной структуры с постоянными по высоте значениями жесткости элементов дискретное расположение ригелей, пе - .ремычек, стержней-связей целесообразно заменять непрерывным (континуальным) расположением, сохраняя ^дискретное расположение стоек рам, простенков диа - іфрагм. При этом расчетная схема считается дискретно- Йіконтинуальной. Расчеты выполняют на основе общего Дифференциального уравнения (XV.2Q). Усилия, перемещения и динамические характеристики различных многоэтажных зданий определяют по готовым формулам и 'таблицам, полученным в результате решения общего уравнения. Расчетную высоту здания устанавливают по формуле (XV.25); при числе этажей п^ 16 принимают Н=Н0.
Расчетную ветровую нагрузку для зданий высотой 12 этажей и более 40 м при расчете прочности определяют с учетом динамического воздействия пульсаций скоростного напора, вызванных порывами ветра. Кроме того, должна быть выполнена проверка ускорения колебаний многоэтажного здания при порывах ветра, которое ограничивается а^15 см/с[3].
Прогибы многоэтажного здания определяют от действия нормативной ветровой нагрузки. Прогиб верхнего яруса ограничивают значением, равным /^Я/1000.
Горизонтальную ветровую нагрузку (увеличивающуюся кверху) при расчете многоэтажных зданий заменяют эквивалентной, равномерно распределенной или же эквивалентной нагрузкой, распределенной по трапеции. При равномерно распределенной нагрузке получают более компактные расчетные формулы и практически точные значения перемещений и усилий в расчетных сечениях. Эквивалентная, равномерно распределенная ветровая нагрузка определяется по моменту в основании
•где Масі 84—943
Р = 2Mact/H2, (XV. 48)
— момент в основании от фактической ветровой нагрузки.
Обозначения жесткости, усилий и перемещений при изложении теории расчета многоэтажных зданий содержат индексы иа основе латинских корней в соответствии с главой СНиП «Бетонные и железобетонные конструкции» и международным стандартом № 3898 «Обозначения и основные символы»: Ьт — балка, ригель; cm — комбинированная; dg— диафрагма; fl — перекрытие; т — рама; ft—фундамент; /п — стык; It— перемычка; рс — сборный; st — система; col — колонна.
(XV.20) и его решение согласно (XV.23). Краевые ус - ШОвия задачи
1) w (0) = 0; 2) w' = 0; 3) - а/"<0) = Q0(0); 4) —Ш"(Х) = 0.
(XV «50)
При равномерно распределенной нагрузке р(х)=р момент и поперечная сила
М„=-0,5рЯ? (1-І)2; (?0 = рЯ(1-|). (XV. 51) Тогда С0 в решении (XV.23) принимает значение
Psl ф2 p$|W-l) /|2 g,
(XV. 52)
0 2v2 2v2 V 2 3 12
Из решения системы линейных уравнений находим
С1 ==— С3 =— PS2 x/v2; C4=-S2C2=-"SlWv2'
Ю
+ - ТГ)].
Уде X = (1 +Я, slU)/ch К.
Уравнение перемещений после подстановки в (XV.23) значений постоянных интегрирования Сі принимает вид
Р4 г ф2 = —— Хф — - г— + хсЬф — Xshqp — v; L і
(XV. 53) (XV. 54) (XV. 55)
2 3 12
(XV. 56)
При ф=Х и | = 1 прогиб верхнего яруса
РН*
2 (к — 1)
Я.» (у2 —1)
/ =
(XV. 57)
2v? Я,2 S
При определении усилий учитываем, что dx=Sidy = =Hd% ks2=H; | = фД.
Изгибающие моменты вертикальной связевой диафрагмы
РЯ2
V?
М — w" =-
(1-і)? (V?-1)-
(XV. 58)
Я,2
■ (1 — к ch Ф + X sh Ф)
Поперечные силы вертикальной связевой диафрагмы
(1— Ј)(v? —1) + сЬф— Y"sh(P ]• (XV.59)
РН_
V?
Q = АГ =
531
Поперечные силы стоек рам
Q/r = Qo-Q = -^(i-S + -^sh<P-chq>): (XV.60)
Продольные силы крайних стоек рам определим из уравнения равновесия
N = ■
(XV.61)
1)! +
1
+ —— (1 — х ch ф + К sh ф)
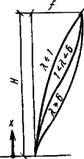
Рис. XV.34. Зависимость линии изгиба рамно-связевой системы от характеристики жесткости
А.
Изгибающие моменты М и поперечные силы Q распределяются между отдельными диафрагмами системы пропорционально их изгибным жесткостям.
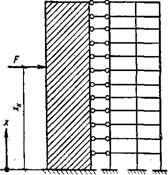
Рис. XV.35. К определению перемещений рамно-связевой системы от действия горизонтальной силы
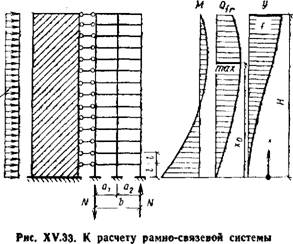
Эпюры усилий и перемещений рамно-связевой системы изображены на рис. XV.33. На эпюре поперечных сил максимум Qfr будет в сечении с координатой ф0, где
<?;,=-l+xch?0-bchf0 = 0. (XV.62)
Обратим внимание, что при ф=Х поперечная сила QfrҐ=0. Поперечная сила Qfr распределяется между отдельными стойками рамы пропорционально их жесткостям. Изгибающие моменты стоек и ригелей многоэтажной рамы определяют по значениям поперечных сил СО - : гласно способу, изложенному в § XV.3.
„Характер линии изгиба рамно-связевой системы от Р^ризонтальной нагрузки зависит_от характеристики же - Врюсти К. При относительно жестких вертикальных свя - |евых диафрагмах, когда линия изгиба, как и у
Врнсольной балки, обращена выпуклостью в сторону начального положения. С увеличением % линия изгиба ргановится выпукло-вогнутой и при — вогнутой
Ірис. XV.34). Характер линии изгиба существенно влияет на динамические характеристики многоэтажного здания.
Горизонтальные перемещения рамно-связевой системы от действия силы F— 1, приложенной в уровне Xit Кис. XV.35), определяют из решения уравнения (XV.17) рж значениях нагрузки р(х) =0 и момента силы на уча - Ётке равном М0= — (хк— х), и на участке x~^xkt
Вавном Мо=0. Кроме краевых условий привлекаются Условия сопряжения в уровне хк по перемещению, углу щоворота, изгибающему моменту. Тогда из уравнения Перемещений
![]()
Где хі = Фь — эЬфй + (сЬфЛ — l)(sh — th X, ch фг + thX); (XV.64) Vh = xk/s2; <Pj = Vs2-
(XV. 63)
3. Рамио-связевые системы с комбинированными диафрагмами
В рамно-связевых системах со сплошными и комбинированными диафрагмами (рис. XV.36) суммарная из - Гибная жесткость В=В4Є--Вст, с комбинированными — Р**Вст, где Вст — изгибная жесткость сплошной части ргомбинированной диафрагмы.
(XV. 65)
V Сдвиговую жесткость рамной части комбинированной диафрагмы определяют с учетом упругого поворота узла сопряжения стоек и ригелей (рис. XV.37):
3tf (1 + 40)[fr (1 + ч„) + 6»2 (1 + 2г)„)] Цк + зу
Где і і — погонная жесткость ригеля рамной части комбинированной Диафрагмы; »2 — погонная жесткость стойки рамной части комбинированной диафрагмы; И]0=г0/1ш (см. рис. XV.36).
Если рамная часть примыкает к сплошной стороне с SByx сторон симметрично, то значение сдвиговой жестко
сти в формуле (XV.65) удваивают. Если комбинирован ная диафрагма образована двумя крайними простенка ми и средней двухпролетной рамной частью (см. рис XV.36), то значение сдвиговой жесткости в формул (XV.65) также удваивают, но значение i2 берут с коэф фициентом 0,5.
А) о) б)
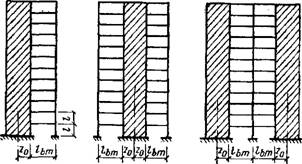
Рис. XV.36. К расчету рамио-связевых систем с комбинированными
Диафрагмами
А—рамная часть диафрагмы расположена с одной стороны; б — тс( же, с двух сторон; в — то же, в центре
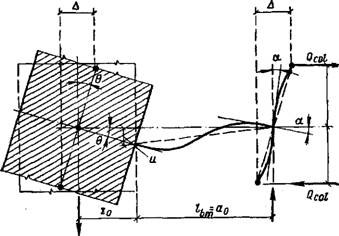
Рис. XV.37. К расчету комбинированной диафрагмы
-^(Сдвиговая жесткость рамно-связевой системы с ком
Иированной диафрагмой равна сумме сдвиговых же - костей рамы и рамной части комбинированной диа - агмы:
К = 12И (S-1 + /--!)+ Кот - (XV.66)
Продольные силы стоек многоэтажной рамы при Ь/<0,7 мало влияют на работу конструкции. Еслипро - |ольные силы стоек в расчете не учитывают, полагая = 1, то усилия и перемещения рамно-связевой систе - с комбинированными диафрагмами определяют по ормулам, полученным выше для рамно-связевых си - ем. Расчет таких систем с учетом продольных сил сто - изложен в п. 7.
Части суммарной поперечной силы Qfr, воспринимае - е стойками рам системы Qfr, c и стойками рамной ча - и диафрагмы Qdg. c, распределяются пропорционально Ишиговым жесткостям:
Qfr, с = Qtr (К - Кст)/К; Qdgfi = Qfr KCJK. (XV.67)
Опорные моменты ригелей рамной части по грани циафрагмы определяют в зависимости от Qfr
М = Зіі (1 + %) (6 + Іі1іг) ;
3 + k/h л
НО оси стоики
З + її/«2 к
І Изгибающий момент стойки рамной части комбинированной диафрагмы равен половине опорного момента ригеля.
|L Связевые системы с однотипными диафрагмами Пр. проемами
І' п
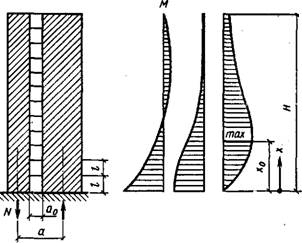
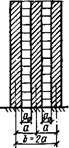
I. Рассмотрим связевые системы с однотипными верти - |альныМй диафрагмами, имеющими различное число ря - ров проемов: один ряд несимметрично расположенных Цроемов (рис. XV.38) или несколько рядов незначительно отличающихся по ширине проемов (рис. XV.39). Вертикальную диафрагму с проемами будем рассмат-
53S
Рис. XV.39. К расчету диафраг* мы
N Mlt
Рис. XV.38. К расчету диафраг* мы с одним рядом иесимметч ричио расположенных проемов
Вh
I
:
1>-1й
А — с двумя рядами проемов; б — с несколькнмя рядами проемов
Ривать как многоэтажную раму, у которой стойками будут простенки, а ригелями — перемычки. Поскольку в такой раме жесткость стоек-простенков во много раз больше жесткости ригелей-перемычек, местным изгибом стоек между узлами в гіределах одного этажа можно пренебречь и при определении сдвиговой жесткости К считать, что 1 Js — величина, малая в сравнении с 1/л Тогда, согласно формуле (XV. 14), сдвиговая жесткость диафрагмы с проемами
/С = 12/-//, , (XV.70)
Здесь г=2іг( — суммарная погонная жесткость перемычек одного яруса диафрагмы с несколькими рядами проемов.
Кроме того, следует учесть, что ригели-перемычки (Олько в пределах проемов имеют конечную жесткость Bit, но в пределах широких простенков становятся абсолютно жесткими. В таких случаях осредненная по все - иу пролету жесткость перемычки составляет Bit у3, где ji=a/a0; а — расстояние лАжду осями простенков; ао— Расстояние между простенками в свету. Погонная жест - Кость перемычки
Ilt =Btt у3/аф.
Коэффициентом ф учитывают влияние деформаций Ідвига перемычки
Ф= 1+2,4 (h/а,)!,
?Де h — высота сечения перемычки.
| Суммарная изгибная жесткость простенков диафрагмы B=1tBj, где Bj — изгибная жесткость отдельного Ьростенка. Если диафрагмы в системе сплошные и с проемами (см. рис. XV.32, б), то суммарная изгибная жесткость Bde+HBh
Изгибную жесткость вертикальной диафрагмы Во (по сечению с проемами за вычетом жесткости простенков относительно своих осей) определяют по формуле (XV.32). Для диафрагм в этой формуле расстояние между осями крайних простенков Ь=Иа, при одном ряде "проемов Ь=а.
(XV.71)
(XV. 72)
В общем уравнении (XV.20) и его решений (XV.23) краевые условия для вертикальных диафрагм с проемами остаются такими же, как и для рамно-связевых си - гстем. Поэтому для расчета диафрагм с проемами следу - г, ет применять уравнения перемещений и прогибов ^(XV.56), (XV.57) и уравнение изгибающих моментов. простенков (XV.58).
![]()
JV=-(1//)J Qitdx,
(XV. 73)
N' I =- (d/dx) J Qlt dx = Qlt. (XV. 74)
Х
Продольные силы крайних простенков вертикальной ; диафрагмы
Н
-V-7
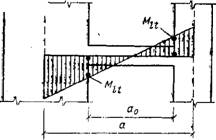
Рис. XV.40. Эпюра моментов перемычки диафрагмы с проемами
1 — с проемами при X— = 1 ...9 Н V2=l, l; 2 — сплошной
Дифференцируя уравнение (XV.61), найдем поперечные силы перемычек
Qtt = (рНІ/Ьч*) (і - і + Y sh ф - ch ф). (XV. 75)
В симметричной диафрагме с двумя рядами проемов поперечные силы перемычек одного яруса равны. В диафрагме с несколькими рядами проемов это равенство принимают как допущение.
Изгибающий момент перемычек по грани проема (рис. XV.40) в предположении, что нулевая точка моментов расположена в середине пролета в свету, равен
Mn = Qlta0f2. (XV. 76)
Эпюры усилий вертикальной связевой диафрагмы с проемами приведены на рис. XV.38. На эпюре распределения Ми координата максимума определяется (как и для рамно-связевой системы) из уравнения (XV.62). Изгибающие моменты отдельных простенков определяют из суммарного момента М пропорционально их жестко - стям.
Согласно уравнению равновесия обобщенных поперечных сил, поперечная сила от действия внешней на - грузки уравновешивается производной от изгибающегс момента простенков и распределенным моментом пере - мычек М, т. е.

Рис. XV.41. Линия изгиба диафрагмы
M'+M = Qoi (XV. 77
Где
M = ZQaaH--=QitbH. (XV.78)
Поперечная сила отдельного простенка
Qj = М' Bj/B + (QM/0(fli + аг)} (XV.79)
Цяесь «і, аг — расстояния от оси простенка до нулевой точки моментов перемычки слева и справа.
Линия изгиба вертикальной диафрагмы о проемами близка по очертанию к линии изгиба консольной балки. На рис. XV.41 изображена линия изгиба диафрагм с
Р
Иапазоном значений характеристики жесткости Х = 1...9 ри v2 = l, l.
Щ Прогиб верхнего яруса диафрагмы с проемами, согласно формуле (XV.57), можно представить как/ ІгИо, т-е - как сумму двух прогибов: іі вызванного податливостью перемычек
I (XV. 80)
11 2v? WBL W J
Вызванного общим изгибом диафрагмы
Здесь изгибная жесткость диафрагмы по сечению с проемами
Bag = v? S/(v?-l) = 50 + B.
: Перемещения 6ik вертикальной диафрагмы с проемами от силы F= 1, приложенной в уровне Хь, определяют, как и для рамно-связевых систем, по формуле (XV.63).
Заметим, что при характеристике жесткости к^З в расчетных формулах усилий и перемещений можно принимать ch X=sh к; к = к.
Установим зависимость между горизонтальными перемещениями диафрагмы и поперечными силами ригелей-перемычек. Для этого составим уравнение равновесия изгибающих моментов ригелей-перемычек и простенков в узлах. Поскольку нулевые точки моментов стоек расположены в середине высоты этажа, а нулевые точки Моментов ригелей — в середине пролета,
2Q0 1/1 = I2Qn а/2,
Отсюда
2а Qu b Qo = Qu— = - (XV.82jf
Полученное значение Q0 подставим в уравнение (XV. 16):
Х
<?tt = 4"/ff'+-ir {Ndx< (XV.83)
Ь в0 J
О f
Отсюда
Х
BQu b С
'-к-Т )Ndx - (XV'84)
О
После двукратного дифференцирования уравнения (XV.84) с учетом, что Qit~N'l, найдем зависимость
5. Данные о параметрах к и v2 из опыта проектирования
Опыт проектирования многоэтажных каркасных зданий показывает, что в рамно-связевых системах характеристика жесткости обычно находится в ограниченном диапазоне: к=0,5...2. Кроме того, из анализа различных конструктивных схем каркасных зданий следует, что при числе этажей до 16—18 в ряде случаев характери-' етика жесткости рам kfr<0,7, т. е. продольные деформации стоек мало влияют на значения усилий и прогибов рамно-связевой системы. Поэтому, когда kfr<0,7, в расчетных формулах усилий и перемещений принимают v2 = 1.
Конструктивное значение вертикальных связевых диафрагм в составе каркаса многоэтажного здания не только в том, что они разгружают каркас, уменьшая часть нагрузки, воспринимаемой рамами (на 10—25%), но главным образом в том, что они качественно изменяют характер эпюры поперечных сил стоек многоэтажных рам: поперечные силы стоек Q;r достигают максимального значения в верхней зоне и уменьшаются к основанию (см. рис. XV.33). Если в рамных системах изгибающие моменты стоек и ригелей от горизонтальных нагру-
ІЦг возрастают книзу, что требует увеличения опорной Шматуры ригелей, а в нижних этажах и увеличения раз - рІеров поперечного сечения ригелей, то в рамно-связевых разбор от — изгибающие моменты в элементах каркаса Іизу уменьшаются, что позволяет сохранить поперечное Учение ригелей и их армирование на опоре постоянны - Цв по всей высоте многоэтажного здания. Следователь - 0, рамно-связевые системы в наибольшей степени от - іечают требованиям унификации и типизации конструк - Йвных элементов здания.
? Опыт проектирования вертикальных связевых диафрагм с проемами показывает, что по соотношению же - £костей простенков и перемычек характеристика жест - рсти % оказывается в диапазоне значений А, = 3...9. При ;£=12...15 влияние податливости перемычек незначи - ельно. При малых значениях характеристики жесткости •Я=1...2) перемычки весьма податливы и существенно
І
Їижают боковую жесткость здания. Продольные де - ормации простенков оказывают существенное влияние а работу диафрагмы с проемами и всегда должны учитываться в расчетах. Весьма распространены значения Коэффициента v2 = l, l...l,3, однако возможны и большие %го значения.
Для расчета усилий многоэтажных зданий от горизонтальных нагрузок с применением ЭВМ имеются разработанные программы на основе различных расчетных ^Моделей — метода конечных элементов, дискретно-контп - ЇЯуальной расчетной схемы и др.
Йг,
При проектировании многоэтажных каркасных и панельных зданий, в первую очередь, определяют усилия в расчетных сечениях. Это необходимо и при выборе экономичного варианта конструкции в вариантном проектировании. С этой целью можно воспользоваться приводимыми расчетными формулами и таблицами, полученными из основных формул (XV.57) —(XV.75).
Суммарный изгибающий момент сплошных диафрагм рамно-связевых систем или простенков диафрагм с проемами связевых систем в заделке
/v? —1 ^ р№
~Т~ (XV • ^
Fc If-'
Суммарная поперечная сила сплошных диафрагм рамио-связевых систем или простенков диафрагм с проемами связевых систем в заделке Q—pH или по фактической нагрузке
Q = Qact - (XV.8 7)
Значения М и Q распределяются между отдельными! сплошными диафрагмами и простенками диафрагм с: проемами пропорционально их изгибным жесткостям. ;
Максимальная суммарная поперечная сила стоек рам Qfr = kipH/v*. (XV. 88)*
Максимальная поперечная сила перемычек диафрагмы с проемами
Qu = kipHl/v* ь. (XV.89)
Продольная сила крайних стоек многоэтажной рамы' или простенков диафрагм с проемами в первом этаже
N = (М0 —М)/Ь; М0=—0,5pm. (XV.90)
Прогиб верхнего яруса рамно-связевых систем или простенков диафрагм с проемами связевых систем /va — 1 рН*
Значения коэффициентов а,, а2 приведены в табл. XV.2, коэффициента ki — в табл. XV.3.
Пример XV.1. Определить прогиб и усилия от горизонтальной нагрузки в элементах сборного железобетонного 16-этажного здания, работающего в поперечном направлении по рамно-связевой системе (рис. XV.42). Сетка колонн 6X6 м; высота этажей 1=3 м; высота здания На=48 м. Риге* лн поперечных рам сечением 25 X Х50 см; колонны во всех этажах сечением 45x45 см. В здании запроектированы три поперечные и две продольные диафрагмы толщиной 14 см. Междуэтажные перекрытия из крупных панелей. Стыки и сопряжения сборных элементов выполнены на сварке закладных деталей с замоноличиванием. Класс бетона В25.
Решение. Жесткость железобетонных элементов определялась, как для сплошных бетонных сечеиий. Результаты вычислений жесткости элементов приведены в табл. XV.4.
НЖШЙ
6 '10' 60
Рис. XV.42. К примеру расчета рамно-связевой системы
Изгибная жесткость трех поперечных диафрагм В=3-87:83 К107 = 261 • 107 кН • м2,
ТйШтл ШЖ Значении «(Яффіниюгтот аї й«2 длв определении МІЩШЩЩШтЩШфШЩШЩт,
Вертикальных диафрагм в рамно-связе«ых системах и простенков диафрагм с проемами в связевых система*
|
К |
0 |
0.5 |
0,75 |
1 |
1,25 |
1,5 |
1.75 |
2 |
2,5 |
3 |
І>4 |
|
«1 |
0,5 |
0,48 |
0,445 |
0,41 |
0,377 |
0,351 |
0,32 |
0,3 |
0,261 |
0,232 |
(X—1)Д! |
|
А2 |
0,125 |
0,117 |
0,108 |
0,09 |
0,079 |
0,067 |
0,059 |
0,05 |
0,038 |
0,0298 |
(0,5-аОД? |
Таблица XV.3. Значения коэффициента кх и координаты go для определения максимальной суммарной поперечной силы стоек рам в рамно-связевых системах и максимальной суммарной поперечной силы перемычек диафрагм с проемами в связевых системах
|
% |
0,5 |
0,6 |
0,75 |
І |
1,25 |
1.5 |
1,75 |
S |
2,8 |
3 |
|
Кг So |
0,037 0,93 |
0,052 0,9 |
0,075 0,85 |
0,115 0,77 |
0,153 0,7 |
0,187 0,63 |
0,218 0,58 |
0,247 0,54 |
0,297 0,47 |
0,34 0,38 |
|
Продолжение табл. XV.3 |
||||||||||
|
К |
4 |
5 |
6 |
7 |
8 |
10 |
12 |
15 |
20 |
30 |
|
Ki Іо |
0,43 0,35 |
0,48 0,32 ' |
0,54 0,3 |
0,58 A, 28 |
0,62 0,26 |
0,67 0,23 _ |
0,71 - 0,21 |
0,75 0,1В |
0,8 0,15 |
0,89 0,11 |
Таблица XV.4. Расчетные данные к примеру XV.1
Стойки
Ригели
Жесткость
Изгибная Погонная
Суммарная погонная
Суммарная осевая крайних стоек
В=9,1-104кН-м2 ;=3,03-Ю4кН-м s=73-104 кН-м
£ьЛ=4.3-107кН
В=7-10*кН-м2 ( = 1,17-104 кН-м а= 18,7-104 кН-м
Сдвиговая жесткость многоэтажных рам по формуле (XV. 14)! 12 12-104
= 60-10* кН.
Ї (s-l + /~1) 3 (73-1 + 18.7-1)
Изгибная жесткость многоэтажных рам каркаса по формуле (XV.33)
К
В0 = (1/2) ЕьАУ1 = (1/2) 4,3-107-122 = 310-107 кН-м2.
= 48
48 м.
0,5
Расчетная высота здания по формуле (XV.25) п.„ 16
Я=Я,-
16 — 0,5
Характеристика жесткости многоэтажных рам каркаса по фор< муле (XV.29) Xfr—HyfK/S0=48 / (60-104)/310-107 = 0,67 <0,7; слеі довательио, влиянием продольных деформаций стоек в расчете мож< но пренебречь и далее в расчетных формулах принимать v2=l. Xai рактеристика жесткости рамно-связевой системы по формул^ (XV.24) %=Н/vWB = 48/(l-60-104)/261-107=0,73.
Прогнб здания от нормативной нагрузки fcHI1000. По форму - ле (XV.91) и табл. XV.2 находим f=a2pHlIB= (0,109-484р)/261 >< Х'07 = 2,20 • Ю-4 р р — нагрузка на 1 м высоты и на всю длин} здания.
Усилия в элементах здания определяют от расчетной нагрузка, Суммарный изгибающий момент диафрагм в заделке по формулі (XV.86) н табл. XV.2 М=— ct^2=0,45-482p=—1035р; для одної диафрагмы М=—(1 /3> 1035р =—345р. Поперечная сила диафрагм в заделке Q=pH или от фактической нагрузки Q = Qact.
Суммарная поперечная сила стоек рам (максимальная) по формуле (XV.88) н табл. XV.3 Qfr=Ј1ptf = 0,072-48p=3,46p; для одной рамы Qfr= (1/8)3,46р=0,43р. ;
Продольная сила крайних стоек рам в первом этаже по формулу (XV.90) •
М0—м
I
N :
: — (0,5 — 0,45) 482р/12 =— 9,6р;
Для одной крайней стойки N=—(1/8) 9,6р=—1,2р.
Коэффициент уменьшения жесткости краЙННХ СТОеК При ibm/tcal' -=1,17/3,03 = 0,39, согласно табл. XV.1, 0=0,55.
Q = Qfr
2,1
Поперечные силы: крайней стойки 6 0,55
0,43р = 0, lip;
L + 2p
Ней Q=0,21p.
| Изгибающие моменты стоек рам определяют по поперечным сн-
Q согласно формулам (XV.2), (XV.3). ■ Пример XV.2. Определить прогиб и усилия от горизонтальной узки в элементах сборного железобетонного 16-этажиого здания, тающего в поперечном на - пенни по связевой системе с типиыми диафрагмами (рис. Ц43). Сетка колонн 6x6 м; вы - этажей 4,2 м; высота здания fe67,2 м. Колонны во всех эта - сечением 45X45 см. В здании поперечные диафрагмы с аи рядом проемов и продоль - 'многопролетные рамы. Пересечением 30X120 см. Меж. гажные перекрытия из круп - панелей. Стыки и сопряжения рных элементов выполняют на Ірке закладных деталей с замо - нчнваннем. Класс бетона В25.
Решение. Жесткость железобетонных элементов определялась как
F
Сплошных бетоииых сечеиий: В«=116-104 кН-м2. По формуле
.72) ф = 1 +2,4 (ft/ao)2 = 1 + 2,4 (1,3/5,55)2 =1,13. s С учетом деформаций сдвига В«= 116-104/1,13= 103-104 кН-м2. вісстояиие между осями простенков диафрагм с одним рядом прое - рв Ь=а= 12 м. Пролет перемычки в свету а0=5,55. Отношение feeo/a0=2,16. Погонная жесткость перемычки по формуле (XV.71)
1и = - ЁМ-уг = JHdOL2>163 = 86.10. кН. м*.
А 12
Цвиговая жесткость диафрагм при одном ряде проемов по форму- KJXV.70) К= 12л//= 12-86-104/4,2=247-104 кН.
Изгнбиая жесткость простенков диафрагмы Bi = B2=15,8X і|07.кН-м2.
Суммарная изгибная жесткость двух простенков В=31,6х 110? кН-м2.
Осевая жесткость простенков ЕЬА=3,5-Ю7 кН.
По формуле (XV.33) В0=(1/2)£И&2= (1/2)3,5- 10М22=252Х?107 кН-м2.
Изгибная жесткость вертикальной диафрагмы по сечеийю с прое- юи Bdg=В0+В=283,6-Ю7 кН-м2.

Рнс. XV.43. К примеру расчета связевой диафрагмы с проемами
По формуле (XV.22) v2=l+B/B0= 1+31,6-107/252-107 = 1,125.
= 6,3.
545
Расчетная высота здания прн п=16 составит: Я=Яо=67,2 м. . Характеристика жесткости вертикальной диафрагмы по формуле BV.24)
1,125-247-104 31,6-10'.
-943
Горизонтальная нагрузка р, действующая на одну вертикал - диафрагму, равна 'Д всей нагрузки, действующей на продольн фасад здания ^поскольку все четыре вертикальные диафрагмы здан однотипны). Прогиб диафрагмы определяют действия нормат иых нагрузок, усилия в элементах — при расчете прочности от рас иых нагрузок.
По формуле (XV.91) и табл. XV.2
УЇ— 1 , __ рН4 / i_
M / 1,Г25 ■ v2 "I [8
F= {-:T— + ®2
Pv2
67 24 в + 0'0092) 31,6.107-1,125 прогиб диафрагмы с недеформируемымя перемычками
67'24* — 9 10—4 п-
SBdg 8.283,«.да '
Следовательно, под влиянием податливости перемычек прогиб диа^ рагмы увеличивается в 1,53 раза.
Суммарный изгибающий момент простенков в заделке по фм муле (XV.86)
/v3— 1 рЯ5 П,125 — 1 л Лб7,2»р „^ (— + «,]—=_ +0,134) — =-790,
Для одного простенка А1=—395;?.
Поперечная сила простенков диафрагмы в заделке Q=pH, ил от фактической нагрузки Q — 0мСи
Поперечная сила перемычек (максимальная) по формуле (ХУ.8І и табл. XV.3
Л kjpm 0 ,.55-67,2-4,2?
12-1,125 =П'6Р-
Изгибающий момент перемычек
Продольная сила простенков в первом этаже по формуле (XV.90: Af0~Af 0,5-67,2р-790р
= —у— Іі =" 123Р-
7. Системы с разнотипными вертикальными конструкциями
К системам с разнотипными вертикальными конструі циями относятся: связевые системы с несколькими раЗ ными диафрагмами, имеющими различное число ряд<і проемов; рамно-связевые системы с комбинированным- диафрагмами при учете продольных сил стоек
Мшио-связевые системы, имеющие диафрагмы с проемами, и др. (рис. XV.44). Решают такие системы с помощью общего уравнения (XV.20). При числе разнотипных вертикальных конструкций, равном т, получим синему т дифференциальных уравнений (XV.20) и два добавочных уравнения:
Pi (х) + Рг W+- • • Л-Рт(х) = рЩ M0i + M02+... + M0m=M0. J '
Опыт проектирования показывает, что при большом тесле разнотипных вертикальных конструкций проще
12 к п

Рис. XV.44. К расчету свиаевых систем с Рис. XV.45. К расчету разнотипными вертикальными ионетрукідая - систем с дискретными ми связями
Применять расчетную схему с ограниченным числом дискретных связей между вертикальными конструкциями (рис. XV.45) и решать систему алгебраических уравнений. Практически достаточная точность решения достигается при трех-четырех связях по высоте. При этом единичные перемещения вертикальных конструкций определяют по формуле (XV.63).
Если система состоит только из двух разнотипных вертикальных конструкций, усилия и перемещения можно определять по готовым расчетным формулам. В этом случае система двух дифференциальных уравнений и двух добавочных уравнений (XV.92) сводится к одному дифференциальному уравнению шестого порядка относительно перемещений с четными производными. Учитывая, что суммарный изгибающий момент простенков
М=—By", можно получить дифференциальное урав» ние четвертого порядка, которое для нагрузки р{х) = имеет вид: v
MIV-2a2M" + Ь*М-сМ0 — ер = 0, (ХУ. Щ
Где 2а2 = (1 /В) (v? Kl + v2n K2) (XV.94J
B* = [Kx K2 (B + B„і + Bo2)]/BBoi Ba2 (XV.95|
C= КІ К2/B0i Bo2; e*=KilBA + KtlBtf, (XV.96|
V? = 1 + B/B0l] vj, = 1 + B/B02; (XV.97|
В—суммарная изгибная жесткость простенков и сплошных диафрагм^ К і, Кг, Boi> йог — значения соответствующих сдвиговых и изгибныж жесткостей первой н второй диафрагм; при этом должно соблюдать-! ся условие.
KjBai-K2lBa2^i). (XV. 98)
По значению параметров жесткости конструкций: многоэтажных зданий обычно Ь2<а2. В этом случае ре* шение уравнения (XV.93) имеет вид:
М = рН2 [С! ch <ц х + С2 sh otj х - f С3 ch а2 х - f С4 ch а2 * —
+ (XV. 99)
Где h = c/bt, t2 = (e - 2а2 tJ/НЇ б4; (XV. 100)
«і,2 = * =F W - й4 . (XV. 101)
. Краевые условия:
1) М' (0) = рН . 2) М"' (0) - Ki + K2 М' (0) =0; :
D
3) М (Я) = 0; 4) М" (Я) =— р.
Первое краевое условие обусловлено тем, что угол поворота вертикальных диафрагм в заделке у'(0)=0, отсюда, согласно (XV.17), при нулевом промежутке интегрирования N будет —By"'(0)=Q(v) или М'(0)=рЯ.
Второе краевое условие получено после двукратного дифференцирования уравнения равновесия обобщенных поперечных сил системы М"'+МІ + М"2=0.
С учетом (XV.83) и значений Qu, i(0) = Qu,2(0) =0 получим М"'(0) + (Кі + Кі)у"'=0, отсюда
М"' (0) - Kl + K* М' (0) = 0. в
Третье и четвертое краевые условия не требуют пояснений.
Значения постоянных интегрирования, найденные из решения линейных уравнений, с точностью до множителя рН2:
U, ch А,.. — (/ + — 1) г. ^2 . . ^—1—, . —L; Cz= ^ '(XV. 102]
^1 ch
VS ЦІ2ch >"2 ' 1^2
Где (X = ^ - = аг H Ц = «2 H (XV. 104)
- .Ч^о-Ф - У; = У; (XV. 105)
q = H2 (Кг + K2)/B. (XV. 106)
РН* У= —
Уравнение перемещений системы получим после дву - :ратного интегрирования уравнения изгибающих момен - в (XV.99) и определения постоянных интегрирования Ы условий у {0) =у'{0) =0. Тогда
TOC o "1-3" h z Ci, .Л С.
(1 — ch ах *) —f - + (сех * — ch ах х) +
Ч ' Ч
С с t
+ (l+cha2*)-^-+(a2*-sha2*)-f
Лі 2 V2
-f + l)-^]- (хул07)
Поперечные силы перемычек диафрагм удобнее определять из другого дифференциального уравнения. Запишем уравнение равновесия обобщенных поперечных сил в горизонтальном сечении системы
I, M' + Jix + Mt^ Qo', (XV. 108)
Здесь распределенные моменты перемычек Mi, М2 определяют по формуле (XV.78); в рамно-связевой системе с диафрагмами, имеющими проемы, M2—Qfr, а в рамно - связевой системе с комбинированными диафрагмами Mi = Qag, c, M2=Qfr, c.
С учетом того, что М' = —By'" и что значение у"', Согласно (XV.85), справедливо для каждой диафрагмы с проемами (поскольку их перемещения у равны), получим систему двух дифференциальных уравнений:
(В/КЛ М[ - v'i Ц - М + Q = 0; 1
„ ' _ _ (XV. 109)
Ifi! K^j Vj| М2 - Mj - f - Q0 = 0. j
Для каждой вертикальной конструкции из системы ^равнений (XV.109) получаем дифференциальное уравнение четвертого порядка. Запишем его для первой диафрагмы: _ . _ _
М{v - 2а2 М'[ +blML - d Q0 = 0; (XV. 110)
Здесь 2а2, Ьл сохраняют те же значения, что н в (ХУ.94уУ (XV.95); І
C1 = (l/B2)(v21-ijKjjy (XV,111|
Для второй диафрагмы |
^ = (XV. 1
Решение %..
Л<і = Ci ch af х + С2 sh «і х - f С3 ch а2 х + С4 ch а2 х -f t3 Qa,
(XV. 112]
Где
'.-K-O/Ctfi-O; ,
.і
Для второй диафрагмы J
/,= (v?-l)/(v? v?,-l). (XV.
Краевые условия: 1) Mi(0)=0; 2) K(0) + (1/S) X X^iQo(0)=0; 3) Mi (H) = 0; 4) МЇ (Щ—(ЦВ)
Значения постоянных интегрирования с точностью щ; множителя рН:
~~~ A^j ch Я^
Сз = - % : С4 =- , 3 П ; (XV. 115*
Где 4 = Н3 і^/В; J& = Я2Л2/В. (XV. 1161
При определении постоянных интегрирования второй вертикальной конструкции в формулах (XV.114)', (XV.115) вместо Яоі следует принимать Х02.
По найденным значениям М вычисляют для каждой, диафрагмы изгибающие моменты перемычек, При этом, согласно формулам (XV.76), (XV.78),
Ми = Qit о0/2 = MlaJIb. (XV. 117)
Продольные силы крайних простенков определяют интегрированием уравнения (XV.112). В соответствии с (XV.73) й (XV.78) для крайних простенков каЖДой диафрагмы с проемами
Н
І с - рнг
N=~t) 7-
Сі
(ch — ch «і х) - f - '-і
4- (ch Xf — ch ax x)
-f (sh k2 — sh a2 *) h
+ (ch Я,2 — ch a2 x) + (1 — g)2
A Уі
Сз_ h
+
(XV. 118)
Ло
Пример XV.3. Определить про - • гиб и усилия от горизонтальных нагрузок в элементах 16-этажно - : го здания, работающего в поперечном направлении по связевой системе с разнотипными верти - Гкальными диафрагмами (рис. . XV.46). Сетка колонн 6x6 м; высота этажей 4,2 м; высота здания #о=67,2 м. Диафрагмы с одним н двумя рядами проемов и сплошные. В продольном направлении 'идут многопролетные рамы. Расстояние между осями крайних
Простенков первой диафрагмы Ь=2а=15,55 м, второй — Ь=а= 12 м. Таблица XV.5. Значения жесткости диафрагм
|
Жесткость элементов |
Диафрагма с проемами |
Сплошная |
|
|
Первая |
Вторая |
Диафрагма |
|
|
Суммарная изгибная простенков Изгибная Сдвиговая |
Вх=40,1бХ Х107 кН-м2 Во1=472 X Х10' кН-м? Ki=7l,5x ХІ04 кН |
В2=63,68х ХЮ' кН-м? Во2=500х ХІ0' кН-м? A:z=562x X10* кН |
В<м=31,84х ХЮ7 кН-м? |
Решение. Значения жесткости элементов диафрагм и расчетные параметры приведены в табл. XV.5 и XV.6.
Суммарная изгибная жесткость В=В, +В2+В1(((= 135,68Х ХЮ7 кН-м2. Условие (XV.98): Кх/ВтФКг/Вог, т. е. 1,15-Ю-4^ =уь11,3'Ю-4, соблюдается.
Прогиб верхнего яруса здания при £=1 по формуле (XV.107) /=29,45.10-*
Для расчета моментов перемычек и продольных сил простенков второй диафрагмы с проемами также вычисляют f3, A, q2. Сі,2,з,4.
Заметим, что при шаринрном соединении перемычек с простенками прогиб /=125-Ю-3 (рН*/В), т. е. увеличивается больше, чем в 4 раза.
|
If-- |
Г4- f | 1 С |
|
І Сч 1 ш |
J |1° |
|
"Т |
'Г • t |
|
[ 6<Ю*60 |
Рис. XV.46. К примеру расчета связевой системы с разнотипными диафрагмами с проемами
Суммарный изгибающий момент простенков диафрагм с проемами и сплошных диафрагм определяют в заделке по формуле (XV.99): М=0,22 рН2. Этот момент распределяется между отдельными элементами пропорционально их изгибным жесткостям.
Таблица XV.6. Значения расчетных параметров
Значение параметров
■Vj = 1,29; vfj =1,29 а2=2,98-10—3; &4=1,4-10-6
/і = 122,3-10-3; /2=85,5-10-3
<*!= 15,5-Ю-3; а2=76-10-3
Я, = а, Я=1,041; А2=а2Я=5,11; >.„ = 21,19
Для расчета прогибов и изгибающих моментов простенков:
С, = —86,153-10-3; С2=67,004-10-3 С3=—157,850-Ю-з; С4= 158,244-10~3
Для расчета моментов перемычек и продольных сил простенков первой диафрагмы с проемами:
<з=435-Ю-3; Ащ =2,39
Номер формулы
(XV. 97) (XV. 94), (XV. 95) (XV. 100) (XV. 101) (XV. 104), (XV. 106)
(XV. 102) (XV. 103)
(XV. 113), (XV. 116) (XV. 114) (XV. 115)
С1=—361,524- Ю-3; С2=497,053- Ю-3 С3=—76,138- Ю-3; С4=76,014- Ю-3
Изгибающие распределенные моменты перемычек определяют по формуле (XV. 112): максимальный момент перемычек первой диа« фрагмы М — 0,073 рН при £0 = О,35; максимальный момент перемычек второй диафрагмы Л1 = 0,320 рН при |0=0,35. Затем определяют изгибающие моменты перемычек по грани проема, пользуясь формулами (XV.76), (XV.78).
Продольные силы крайних простенков определяют при х=0 по формуле (XV.118): для первой диафрагмы с проемами N = =—0,06 pH*/b; для второй N=—0,22 рШ/а.
8. Влияние податливости оснований
Под влиянием неравномерного давления основания на грунт происходит крен фундамента и вертикальной диафрагмы. При этом возникают дополнительные перемещения многоэтажного здания. В рамно-связевых системах под влиянием податливости основания увеличивается доля нагрузки, передающейся на рамы, особенно в верхних этажах. Из-за податливости основания под фундаментами колонн также создается дополнительное смещение рамного каркаса, однако влияние его в этой конструкции мало.
Чтобы повысить пространственную жесткость многоэтажных зданий и устранить дополнительные прогибы,
возникающие вследствие податливости основания, необходимо уплотнять грунты основания сваями или прибегать к устройству сплошной фундаментной плиты и т. п. Податливость свайного основания, особенно при сваях - стойках, не существенна.
Под влиянием момента М осадка края фундамента вертикальной диафрагмы (рис. XV.47)
«=±-^-=±2^-7- j (XV. 119)
Отсюда крен фундамента (пренебрегая деформацией са> ного фундамента}.
0 = 2 u/a = M/Bft, (XV. 120)
Где 5/( = Сф/ — угловая жесткость фундамента; Сф—коэффициент постели при неравномерном обжатии основания; I — момент инерции подошвы фундамента; а — размер стороны фундамента в плоскости изгиба.
В связевых системах, с общим фундаментом под всеми простенками диафрагмы дополнительный прогиб под влиянием крена фундамента
/ = 0Я. (XV. 121)
Для рамно-связевых систем в решении (XV.30) следует принять краевые условия с учетом податливости основания: 1) w (0) = 0; 2) w' (0) =— ■ = — ВМ (0)/Bft =Bw" (0)/Bft—
Угол поворота диафрагмы в основании пропорционален изгибающему моменту1;
3) w' (0)/v2 si - ш' (0) = Qq (0); 4) ю" (X) = 0.
Постоянные интегрирования определяют из решения системы уравнений:
С1=-С3=-р4н a0/v2; C2 = ps|X/v2; (XV.122)
Db EH □
|
■ +J і- |
|
|
А |
|
S
Q.
■^щщщщ
Рис. XV.47. К учету влияния податливости основания
:; '.Членом HftQo (0) в выражении изгибающего момента как величиной относительно малой пренебрегают.
4
V2shA ■ 1) Я. Д
]}/(va+ (XV. 123)
(XV. 124)
(v?-
2v?
C4=— РЪ ГГТ^ ї
Где
= + Pi [l
Характеристика податливости основания;
<рЛ = B/HBU - коэффициент податливости основания;
Pf = XshX/(l+XshX); ft^UM/ch*,. (XV.125)
При абсолютно жестком основании ccq=1; q)ff=0.
Р4
Ф2
(у2_!)Х,4
2 V 2
-2_ _L
З ^ 12
+
Уравнение перемещений рамно-связевой системы с учетом податливости основания после подстановки в k(XV.23) значений постоянных интегрирования принимает вид
«о(1 - t-UhA,) — 1
Shq> — ■j. (XV. 126)
■ а0 х ch ф -
ChX,
Определим усилия в элементах конструкции здания с учетом податливости основания. Изгибающий момент диафрагмы
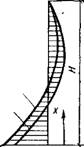
М=-
<*о=а,9
Рис. XV.48. Зависимость эпюры моментов вертикальной диафрагмы рамно-связевой системы от характеристики податливости основания
. И)"
X,2 sh к
(XV. 127)
Поперечные силы вертикальной диафрагмы
(1
Ch ф
«о (1 + к sh А,) -
1
Ftshi,
VS [ 2 v
X (1 — а0 «ch ф)
«а (1 + к ch Я,) — 1 А,? сЬЛ,
|)2(V2_1)_J_X
0% + «о к ch к — 1
Sh<p
Поперечные силы стоек рам рн_ Г, «о х
B(v!-1) + a&it
•sh
(XV. 128)
Sh ф ■
Ch<pj. (XV. 129)
Под влиянием податливости основания уменьшается характеристика ао и уменьшаются изгибающие моменты в основании вертикальной диафрагмы (рис. XV.48),
Пример XV.4. Определить прогиб и усилия от действия горизонтальной нагрузки в элементах 16-этажного здания, работающего в поперечном направлении по рамно-связевой системе, с учетом податливости основания по данным примера XV. 1. Размеры фундамента поперечных диафрагм 2X16 м; коэффициент постели при неравномерно обжатом грунте Сф=0,5 МПа см-1, или 5•Ю-4 кН/м3.
Решение. Угловая жесткость фундаментов трех диафрагм
В}( = С^/ = 3-5.104(2-163)/12 = 10,2-Ш7 кН-м.
Коэффициент податливости основания по формуле (XV.124)
Ф и = B/(HBft) = 261 • 107 / (48 • 10,2-10') =0,53;
Прн Л,== 0,73; chA,= 1,28; shA=0,73 по формуле (XV.125) р, = 0,38; р2= =0,48 н по формуле (XV.55) и=1,24; характеристика податливости основания по формуле (XV.123) прн v2=l
1 +0.53-0,38 _ 0 1 + Ф/<б2 1 +0,53-0,48 ' '
=6,05- Ю-4 р;
Прогиб здания, согласно формуле (XV.126), при <р=Х, 2 («о х — 1)
РЯ4
X2
' 2 к* В
Следовательно, в сравнении с прогибом /=2,20-Ю-4 р под влиянием податливости основания прогиб здания увеличивается в 2,75 раза.
Изгибающий момент в заделке диафрагмы, согласно формуле (XV.127), при ф=£=0, v2 = l будет:
Ot„ у, — 1 М =- рШ 0 =- 783р;
Для одной диафрагмы М=—261 р в сравнении с изгибающим мо- шеитом при неподатливом основании Л1=—345 р (уменьшение на 24%).
Поперечные силы стоек рам Qjr определяют в нескольких сечениях по высоте, пользуясь формулой (XV.128).
Пример XV.5. Определить прогиб от горизонтальной нагрузки 16-зтажиого здания, работающего в поперечном направлении по связевой Сйстеме, с учетом податливости основания по данным примера XV.2. Размеры фундамента, общего под обоими простенками диафрагмы, 2,8X20 м; коэффициент постели прн неравномерном обжатии грунта Сф= 0,5 МПа-см-1, илн 5-10~4 кН/м8.
Решение. Угловая жесткость фундаментов диафрагмы fl/i = Сф/= =5-10* (2,8-203)/12= 10,5-Ш7 кН-м.
Изгибающий момент в заделке диафрагмы А4=рЯ2/2=67,22 р/2 = = 2250 р (знак минус опущен).
Креи фундамента по формуле (XV.120) 0=М/В/4=2250/10,5Х Xi07=2,15-!0-s р.
Дополнительный прогиб диафрагмы под влиянием крена фундамента по формуле (XV. 121) /=в#=67,2-2,15- 10_sp= 14,5- Ю-4 р.
Суммарный прогиб /=13,9-10-'р+14,5-10"1 р=28,4-10-4р. Следовательно, под влиянием податливости основания прогиб здания увеличился в 2,05 раза.
0. Влияние прогиба перекрытий при изгибе в своей плоскости
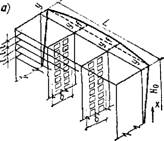
В связевых системах при действии горизонтальных нагрузок прогиб перекрытий при изгибе в своей плоскости может стать соизмеримым с прогибами вертикальных диафрагм, если последние будут размещаться иа Относительно больших расстояниях (рис. XV.49). В этом
Fyj0.5p(xH Ц5рг(»)1
Б)
10,5р, т і ргШ
T 1 Ргі
Ж
Рт
Fftj
Тзґ
Р(*)1
Рнс. XV.49, К пространственному расчету многоэтажного здании с учетом прогиба перекрытий в своей плоскости
Случае крайние вертикальные диафрагмы разгружаются, средние пригружаются и система перестает работать по плоской расчетной схеме. Заметим, что распределение нагрузки между диафрагмами с проемами, пропорциональное Moj, или между сплошными диафрагмами, пропорциональное жесткости В,, происходит только при абсолютно жестких перекрытиях.
Пусть перемещения крайних диафрагм равны у, средних диафрагм y--f. Прогиб междуэтажных перекрытий в своей плоскости / для здания длиной L и шириной h от равномерно распределенной горизонтальной нагрузки интенсивностью р(х) 1/L и сосредоточенных сил — реакций крайних и средних диафрагм — определим как для однопролетной балки. Реакции при трех вертикальных диафрагмах составят: в крайних сплошных диафрагмах 0,5 р(х)1, в средней диафрагме с проемами Рі{.х)і, при
||>том pl(x)+p2(x) —P(x). Тогда прогиб перекрытий IL3 Г 5p(x) _ p2U Bji [ 384 48
Где
' C= (<ҐdgBfl)/lL3- (XV. 131)
Отпор перекрытия; Bfi — жесткость перекрытия при изгибе в своей плоскости, котораи должна определяться с учетом деформаций сдвига, делением иа <p=I+2,4(ft/L)2; а=0,38 и ф^«=48 — числовые коэффициенты. При четырех вертикальных диафрагмах а = 0,27; Ф<г« = 64,8.
Реакция р(х) в выражении (XV.130) зависит от соотношения упругих и геометрических характеристик горизонтальных и вертикальных диафрагм. Поскольку pi(x)=Bиз (XV. 130)
F = [5ji/IV - ар (х)]/С, (XV. 132)
Где 51—суммарная изгибная жесткость сплошных крайних диафрагм;
Тогда из (XV. 132) найдем
У™ = (1/Sj) [ар (х) + СЛ. (XV. 133)
Уравнение равновесия обобщенных поперечных сил в горизонтальном сечении здания с крайними сплошными диафрагмами и средними с проемами имеет вид
- Bty'" - В2 (у'" + Г) + М = Q0; (XV. 134)
Здесь Вг — суммарная изгибная жесткость простенков средних диафрагм.
После преобразования уравнения (XV. 134) с учетом (XV.83) и дифференцирования по х
ВуІУ + В^-К(у" + f )-(K/B0)Nb-p(x) = 0, (XV. 135) где 5 = 5j + В2.
Из уравнения моментов в горизонтальном сечении Nb = М0 - М = М0 + By" + Brf". (XV. 136)
После подстановки в уравнение (XV.135) выражения Nb по (XV. 136) и значения f по (XV. 132) для распределенной нагрузки р(х), изменяющейся линейно, получим обобщенное уравнение изгиба пространственной системы
BiB2 VIII B1Kv0 . и IV „ г " - у ——-—yvl + ByiW — Kv'y —
— КМд/В0 — р (х) = 0, ' (XV. 1.37)
IL3 Г bp (x) p2(x) ] Pl(x) - ap (x)
'= І ЧГл ~~ ^ І= q s (AV. ldU)
Где vg=l+5/B0. (XV. 138)
Обратим внимание аа то, что нз обобщенного уравнения (XV.137)*b частном случае, когда перекрытия абсолютно жесткие и С->оо, можно получить уравнение (XV. 19) для плоской расчетной схемы.
Если учесть, что Ву"=—М, то уравнение (XV. 137)' можно также привести к моментному уравнению шестого порядка.
При сплошных крайних и средних вертикальных диафрагмах уравнение (ХУЛ 35) принимает вид
Bylv + В2 fIv - р(х)= 0. (XV. 139»)
После подстановки в уравнение (XV. 139) значения yiY по (XV.133) получим уравнение прогибов - перекрытий как функцию координаты х по высоте здания:
B*fVv+"if"1- Iі - іг) ■"w=(XV-140)
Уравнение (XV. 140) представляет собой уравнение балки на упругом основании с коэффициентом постели С (см. гл. XII); оно приводится к виду
( s}/4) /IV + f - (ц/С) р (х) = О, (XV. 141)
Где 4Вфг/ВС — линейная характеристика; (XV.]42)
P,= 5i/52 — а. (XV. 143)
Если балка на упругом основании длинная (Я= = то уравнение (XV.141) имеет решение
F = СіЧі + С2т]2 + (ц/С) р W, (XV. 144)
Где "Пі = е-ф cos ф; т]2 = е-ф sin ф; ф = x/sj.
Краевые условия: 1) f(0)=0; 2) f'{0)= 0.
Постоянные интегрирования:
С. . С2 = - fp (0) + згр' (0)]. (XV. 145)
Решение (XV. 144) с учетом (XV.145)
F = (ц/С) [р (х> - ПзР (0) — 42%р' (0)], (XV. 146) где Г)з=г)1 + Т12.
Прогиб перекрытий при равномерно распределенной нагрузке
/= (ц/С) р(1 — *1з). (XV. 147)
Нагрузки, передакщиеся на крайние и средние диа-
Іфрагмде, найдем нз выражения (XV.130) с учетом -(XV. 143), (XV. 147):
Й=(Ві/Л-П#)р; Рг={В2/В + цз11)р. (XV. 148)
Заметнм, что если безразмерная координата ф>1,5, то параметр rjs-»-0, и тогда нагрузка между диафрагмами распределится только пропорционально их жестко - стям, т. е. как при плоской расчетной схеме. Следовательно, с увеличением числа этажей и увеличением ф влияние изгиба перекрытий в своей плоскости затухает, ; как затухают перемещения длинной балки на упругом основании. Прогиб перекрытий в своей плоскости в сравнении с прогибом вертикальных конструкций становится величиной малой.
Граничное число этажей п, при котором работа здания начинает описываться плоской расчетной схемой, исходя из значения составит
П = Н/1 == kSi/l = (3/oV 4BtB2/BC. (XV. 149)
В регулярных зданиях связевой системы с тремя-че - тырьмя вертикальными диафрагмами по соотношению значений жесткости диафрагм и междуэтажных перекрытий часто п = 12...14.
Влияние податливости стыков сборного железобетонного перекрытия при изгибе в своей плоскости можно оценить исходя из кривизны оси при изгибе:
1/р = А! (1/5 + 1/аС/;), (XV. 150)
Где В=0,Р5ЕьІь', а — расстояние между стыками панелей в направлении L; Сп — коэффициент жесткости стыков сборного перекрытия (определяемый из опытов).
Отсюда жесткость сборного перекрытия при изгибе в своей плоскости
Bfi = B/(l+B/aCfi); {XV. 151)
В расчетах конструкций, как показали исследования, можно принимать Bfi=0,7 В.
10. Динамические характеристики
Рамно-связевые системы. При свободных горизонтальных колебаниях зданий нагрузкой являются силы инерции массы. Из уравнения (XV.26) при малом влиянии продольных деформаций стоек, когда v2 = l (т. е.
При kfr<.0,7), получим уравнение свободных колебаний' рамно-связевой системы:
Дх1 дхЪ I dtl '
Подставив у=ХТ, получим обыкновенное дифференциальное уравнение
Xіv - 2а2х" - Ь*Х = 0, (XV .153)
Где 2а? = К/В-, Ъ4 = a? m/Bl. (XV. 154) Характеристическое уравнение
Г* — 2а2г* — Ь* = О (XV Л 55) имеет корни: п = —r2 = a\ r3=—ri=ia2,
Где аі2 = VVa4 + б4 ± а?.
Решение уравнения (XV.153) представляет собой уравнение форм свободных колебаний
X = Сі ch ocj* + С2 sh otj* + C3 cos <x2* + Cs sin ajX. (XV. 156)
Краевые условия:
1) X (0) = 0; 2) X' (0) = BX"/Bit; 3) BX" (H) = 0;
4) KX' (H) — BX'" (H) = 0.
Отсюда получаем систему четырех однородных уравнений:
1) Сх + С3= 0; 2) С^+С.^-С^^ + С^^-О;
3) C^i ch ^ + С2 ^ sh Х1 — сз ^ cos ^ — С4 ^ sin Х2 = 0;
4) С1X2 sh ^.j + С2Х2 ch Xt + Сги sin Х2 — СіХі cos X2 = 0; здесь Яі = аі#; >.2=«2H.
Раскрывая определитель системы уравнений и приравнивая его нулю, получаем уравнение частот с неизвестными Хі и Х2
D (to) = kft (Я,, + (Я, sh ^cos Х2 — sin ch + -1- 21 Х + (&,} + ch Xt cos Х2+ Х1Х2 (xf — sh ^ sin Х2 = 0.
(XV. 157)
В качестве второго уравнения для нахождения Xi и %2 необходимо привлечь свойство корней характеристического уравнения (XV.155), согласно которому
А2 - а2 = 2а2 или Х — Х22 = Xі. (XV. 158)
Согласно другому свойству корней характеристического уравнения,
А2а2 = 64 или Ь? А| = 64Я4;
Отсюда
Ь4 = if (XV.159)
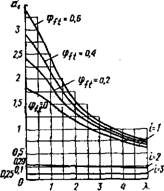
Для практических расчетов при проектировании совместным решением уравнений (XV.157) и (XV.158) в зависимости от различных значений характеристики жесткости К и коэффициента податливости оснований tp/f найдены произведения АДг, а по ним —значения йг=2п/ /2АД2. Период свободных горизонтальных колебаний рамно-связевой системы для трех первых тонов, согласно формулам (XV.154) и (XV.159),
Tt = at № Vm/Bl; і = 1, 2, 3; (XV. 1G0)
Здесь di—коэффициент, определяемый по графику (рис. XV.50); В— изгибная жесткость сплошной диафрагмы.
Податливость основания, как следует из графика, влияет только на первый тон свободных колебаний. Влияние жесткости заполнения каркасного здания {стеновых панелей, внутренних перегородок, облицовок и т. п.) при определнии периода свободных колебаний, согласно опытным данным, может учитываться в расчете увеличением сдвиговой жесткости К в 1,5—2 раза.
Связевые системы. Уравнение свободных горизонтальных колебаний вертикальных диафрагм с проемами связевых систем с учетом влияния продольных сил простенков также можно получить из уравнения (XV. 19) после подстановки в него выражения нагрузки рх= ——md2y/ldt2. Для практических расчетов систему є распределенной массой заменяют дискретной системой с сосредоточенными массами и ограниченным числом степеней свободы. Здание по высоте разбивают на k равных участков, в центре которых сосредоточивается распределенная масса. С помощью единичных перемещений бій для системы с 10 степенями свободы составлено уравнение частот, и из его решения найдены периоды и формы свободных колебаний. Период свободных горизонтальных колебаний вертикальных диафрагм с проемами для трех первых тонов
Т
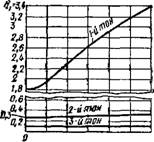
Ті = аг НіУ m/Bl ; <=1, 2, 3; (XV. 161)
38—943
0,1 0,2 0J
Рис. XV.50. К определению периодов свободных горизонтальных колебаний рамно-связевых систем
Рис. XV.52. К определению ю риодов свободных горизонталь иых колебаний связевых дна фрагм с учетом податливості основания
10 11 12 13 НЛЧТ
^ =1,3
Зт>г=ї,2 ІіЧ
10 77 1} 13 14 1-15'
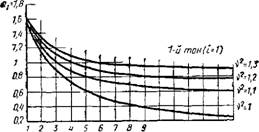
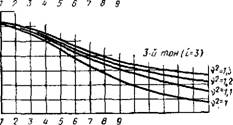
Phc. XV.51. К определению периодов, свободных гори-' зонтальных коле - * баиий трех первых тонов диафрагм о проемами
At — коэффициент, определяемый по графику (рис. XV.51); В — «марная изгибная жесткость простенков вертикальной диафрагмы. Для сплошных вертикальных диафрагм связевых си - гем при учете влияния податливости основания уравне - іе формы свободных колебаний имеет вид
(XV. 164)
Х= Ci chocx-f C2sh ах + Сг cos ах + СА sin ах, (XV. I62)
Аде « = /<в*тт 5 (XV. 163)
I'
В — изгибная жесткость сплошной диафрагмы.
£ Краевые условия: 1) Л"(0)=0; 2) Х'(0)=ВХ" {Щ/ |ІВи-, 3) ВХ"(Н)= 0; ВХ"'{Н) =0.
Отсюда получаем систему четырех однородных урав - й:
І 1) Сх + Сз^О; 2) C2 + C4-(Ci-C3)X^/f =0; I 3) Сі ch li - f C2 sh Xi — C3cos Xt — Ct sin Xi = 0; I 4) Cl sh кг - f Cz ch Xi + C3 sin Яі — C4 cos Xt = 0,
Г
Еэдесь Xi ~aH.
І После раскрытия определителя системы однородных ^уравнений получаем уравнение частот
D (со) = 1 - f chXj cos Xi — kft Xi (chXi sin J^ — sh cos >,j) — 0,
(XV. 165)
Из решения которого находим ІЦ и значения а.
Период свободных горизонтальных колебаний сплошных диафрагм связевых систем для трех первых тонов
Ті = at Ж VmlBl ; і = 1, 2, 3; (XV. 166)
"значения &і определяют по графику (рис. XV.52).
Податливость основания, как следует из графика, влияет лишь на первый тон свободных колебаний вертикальной диафрагмы.
503
Период колебаний основного тона вертикальной диафрагмы с проемами связевой системы (если фундамент под простенками общий), а также период колебаний рамно-связевой системы с учетом влияния продольных сил стоек можно также определять по формуле (XV. 166). ІС этой целью необходимо найти изгибную жесткость ^.диафрагмы с проемами связевой системы или изгибную жесткость сплошной диафрагмы рамно-связевой системы, эквивалентную жесткости сплошной диафрагмы по прогибу верхнего яруса от распределенной нагрузки Bag. Тогда с учетом, что прогиб сплошной диафрагмы
36*
f=pH*/8Bdg, а прогиб указанных систем определяется ri общей формуле (XV.57), найдем
V2Jl*
4Ь!-8(х-1) + (*-1)Ь. ' (ХУЛ67
Здесь В — суммарная изгибная жесткость простенков диафрагмы с| проемами или изгибная жесткость сплошной диафрагмы. ^
Полученное расчетное значение Bdg следует подстав«| лять вместо В в формулу (XV. 166). |
Пример XV.6. Определить период свободных горизонтальных ко.| лебаний 16-этажного зданйя, работающего в поперечном направлені иии по рамно-связевой системе, по данным примера XV.1. Ярусная! нагрузка от одного этажа (включая колонны, стены и полезную на-1 грузку) Q=5500 кН. ■ J
Решение. При значениях характеристик жесткости рамно-связе-1 вого здания Я=0,73,- коэффициентов v2=l и ф/<=0 по графику рис.^ XV.50 находим Оі = 1,65; а2=0,25; а3=0,1. і
Вычисляем период колебаний трех первых тонов по формуле* (XV. 160): "-.
Тг = а, т Л/= 1,65-48? і/ f, 0 f ^ , 0 = 1,03 с5 і
1 1 у BI V 9,81-261 • 107-3
Т2 = 0,156 с; Т8 = 0,063 с.
При податливом основании и значении коэффициента ф/( = 0,53 (пример XV:4) по графику рис. XV.50 находим а{=2,7 и по фор-, муле (XV.160) Гі = 1,68 с; периоды колебаний высших тонов при^ податливом основании не изменяются. .,
Пример XV.7. Определить период свободных горизонтальных ко-1| лебаиий 16-этажного здания, работающего в поперечном направлении по связевой системе, по данным примера XV.2. Ярусная нагрузка от одного этажа (включая колонны, стены и полезную нагрузку) Q = = 12 000 кН.
Решение. При значениях характеристики жесткости диафрагмы с проемами А,=6,3 и коэффициента v2= 1,125 по графику рис. XV.51 находим аі=0,8; О2=0,082.
Г>= ^-/-§- = 0,8.67,2* j/-
Вычисляем периоды колебаний трех первых тонов прн суммарной жесткости простенков четырех диафрагм В=4-31,6-10'= 126,4Х ХЮ7 кН-м2 по формуле (XV.161):
12000 ^ ,81-126,4-ЮМ, 2 ' С* 7*2 = 0,41 с; Г3 = 0,18 с.
Коэффициент формы колебаний. Для расчета многоэтажных зданий на динамические воздействия необходимо определять коэффициент формы колебаний, выражение которого при постоянных ярусных массах имеет вид
: I — номер тона колебаний; k — номер этажа, в котором опреде - ся значение коэффициента формы; / — номер любого этажа; л— во этажей.
А) г б) 1
А —связевых систем и рамно - связевых систем при Я<1; б — рамных систем; в — рамно-связевых систем при
Для регулярных конструкций суммирование можно аменить интегрированием, тогда выражение коэффици - нта формы колебаний принимает вид / і і і
4,k =^Xih^XiCllJj jxfdt.
(XV. 169)
В зависимости от конст - уктивно-расчетной схемы ногоэтажного здания фор - у свободных колебаний Первого тона можно аппроксимировать близкими по |чертанию кривыми. Так, |&ля связевых, а также для рамно-связевых систем с Характеристикой жесткости (рис. XV.53, а) можно Принять
Х= 1 — соз(|я/2); (XV. 170) цля рамных систем (рнс. XV.53, б)
Х = sin (£л/2); (XV. 171)
Для рамно-связевых систем при 1 (рис. XV.53, в)
Х = (1/2)(1 —соз|я). (XV. 172)
Для прямоугольных и квадратных в плане зданий башенного типа с центром масс, совпадающим с центром жесткости, учитывается только первая форма свободных горизонтальных колебаний, соответствующая поступательным перемещениям в каждом взаимно перпендикулярном направлении.
Таблица XV.7. Значения постоянного множителя Ai
Для определения коэффициента формы колебаний в зависимости
|
Системы |
|||||
|
Коэффициент |
Рамио-связевые при |
||||
|
Связевые |
. . . 6 |
%> 6 |
Рамиые |
||
|
1,6 |
1,6 |
1,654—0,054 |
1,33 |
1,27 |
Коэффициент формы колебаний, согласно выражя нию (XV. 169), с учетом (XV.170) — (XV.172) |
Чік = ЛХ, (XV- 17І
Здесь Аі — постоянный множитель, определяемый по табл. XV.7, |
11. Динамические воздействия порывов ветра |
Ч
Ветровая нагрузка на многоэтажное здание опредеі ляется как сумма статической и динамической составляз ющих. Статическая составляющая соответствует устано] вившемуся скоростному давлению и учитывается в расі четах во всех случаях. Динамическая составляющая вызывается пульсациями скоростного давления при поры вах ветра и учитывается при расчете многоэтажных зда^ ний высотой более 40 м в зависимости от периода сво-; бодных горизонтальных колебаний здания.
Нормативное значение статической составляющей ветровой нагрузки определяется по формуле
= (XV. 174]
Где qo — скоростное давление ветра, определяемое в зависимости от географического района; k — поправочный коэффициент на возраста^ ние скоростного давления в зависимости от высоты и типа местности^ тип А —открытые местности, тип Б—города, лесные массивы и тому подобные местности, равномерно покрытые препятствиями высотой более 10 м, тип В — районы крупных городов, имеющие не ме нее 50% зданий высотой 8 и более этажей (табл. XV.8); с—аэрф динамический коэффициент для зданий, принимаемый равным 1,4.
Таблица XV.8. Коэффициент к, учитывающий возрастание скоростного давления по высоте
|
Тип местности |
Высота над поверхностью земли, м |
||||||
|
10 |
'20 |
40 |
60 |
100 |
200 |
350 и выше |
|
|
А |
1 |
1,25 |
1,55 |
1,75 |
2,1 |
2,6 |
3,1 |
|
Б |
0,65 |
0,9 |
1,2 |
1,45 |
1,8 |
2,45 |
3,1 |
|
В |
0,3 |
0,5 |
0,75 |
1 |
1,4 |
2,2 |
3,1 |
Нормативное значение динамической составляющей ветровой нагрузки определяется для каждой і'-той формы колебания в виде системы инерционных сил, приложенных к середине участков, на которые условно разбивает - здание. Инерционная сила, приложенная в середине астка с номером j, определяется по формуле
Е Mj — масса /-го участка, сосредоточенная в его середине; — оэффициент динамичности; хц — приведенное ускорение середины го участка; v — коэффициент, учитывающий пространственную кор - ляцию пульсации скорости ветра по высоте и фронту здания.
X Коэффициент динамичности |<и определяют по графику норм в зависимости от параметра et = Ttv/1200, (XV. 176)
Где Ті — период свободных колебаний многоэтажного здания;
V — 4 Ууп 7/ <70—расчетная скорость ветра; (XV. 177)
Р» — коэффициент надежности по назначению здания; у}=,2 — коэффициент надежности по нагрузке.
| Приведенное ускорение
J (XV. 178)
Здесь п — число участков, на которое разбито здание; Qn — равнодействующая нормативной ветровой нагрузки на k-й участок; т*— коэффициент пульсации скоростного напора ветра для середины й-го ^частка, принимаемый по табл. XV.9.
'Таблица XV.9. Коэффициент тн пульсации скоростного напора »етра для середины k-ro участка
|
Тип местности |
Высота от поверхности земли, м |
||||||
|
До 10 |
20 |
40 |
60 |
100 |
200 |
350 и выше |
|
|
А Ї Б т В |
0,6 0,88 1,75 |
0,55 0,75 1.4 |
0,48 0,65 1,1 |
0,46 0,60 0,97 |
0,42 0,54 0,82 |
0,38 0,46 0,65 |
0,35 0,4 0,54 |
Таблица XV.10. Коэффициент к, учитывающий форму свободных горизонтальных колебаний многоэтажного здания и характер изменения коэффициента пульсации по высоте
|
6=х/Н |
0,1 |
0,2 |
0,3 |
0,4 |
0.5 |
0,6 |
0,8 |
0,9 |
1 |
|
X |
0,34 |
0,52 |
0,66 |
0,7 |
0,9 |
1 |
1,1 |
1,19 |
1,36 |
' Нормативное значение динамической составляющей Эетровой нагрузки для многоэтажных зданий с ярусны-
Таблица XV.11. Коэффициент v, учитывающий простраиствеину корреляцию пульсации скорости ветра
Высота сооружений м
Ми массами, постоянными размерами сторон в плане Ц постоянной по высоте жесткостью может определяться только по первой форме свободных горизонтальных ко-* лебаний
К = wnn *vSdi тп!
Где х — коэффициент, учитывающий форму свободных горизонтальных колебаний многоэтажного здания и характер изменения коэффициента пульсации по высоте и принимаемый по табл. XV.10;
—коэффициент динамичности по первой форме колебаний; коэффициент тп принимается для верха сооружения; коэффициент v определяется по первой форме колебаний по табл. XV. ll; w%n—нормативное значение статической составляющей ветровой нагрузки для верхнего этажа.
Расчетная интенсивность ветрового давления
^К'+^ї,?,,. (XV. 180)
Ускорение колебаний верхнего этажа здания а на основе зависимости между силой, массой т. и ускорением при коэффициенте пульсации 0,2 составит
А = 0,2ш*' т)1п Ll/m, (XV. 181)
Здесь — расчетная статическая составляющая ветровой нагрузки в верхнем этаже; L — длина здания в плоскости, нормальной к действию ветра; т]іп — коэффициент фйрмы колебаний, определяемый по формуле (XV.173).