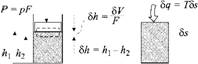Немного об энтропии
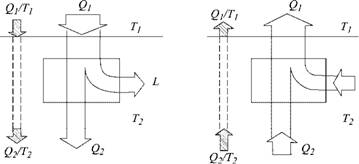
Начнем с того, что вернемся к понятию теплорода (у Карно французское слово calorique — «калорик») и представлению о том, как он создает работу (рис. 3.1).
Мы уже говорили о том, что такое понимание связано с теорией о некоем веществе, которое протекает сверху вниз (от высокой температуры к низкой), производя работу; при этом его количество не меняется. С установлением механической теории тепловых явлений это представление, естественно, отпало.
Однако оказалось (как это часто бывает), что в представлении о том, что сквозь двигатель проходит поток «чего - то», не меняющего при его работе свое значение, есть некое рациональное зерно.
Действительно, вникнем немного глубже в уравнение, отражающее принцип Карно, установив из него связь количеств теплоты Q и Q2 и температур Т и Т2. Для этого преобразуем его. Очевидно (по закону сохранения энергии — первому закону термодинамики), что Q2 = Qi — L тогда основное уравнение Карно можно переписать, заменив работу L на ее значение, так:
Q2 = Ql-Qlr(3-2) J-1
Или, после упрощений:
Qi Q2
Щ = Щ. (3.3)
Выходит, что отношения количеств теплоты к соответствующим температурам (так сказать, «приведенная» теплота) и на входе теплового потока, и на выходе равны. Значит, действительно, есть тепловая величина, отличающаяся от «просто» теплоты, сохраняющая для двигателя постоянное значение в процессах ее подвода и отвода!1.
Замечательное свойство величины Q/T сохраняется и в другом, тоже достаточно важном случае.
Мы уже говорили о том, что двигатель, введенный Карно, — идеальный, т. е. работает без потерь. Это означает, что работа, получаемая от него, максимальна при данных Qі и температурах Т и Т2, т. е. полностью соответствует величине L в формуле (3.1), Если использовать полученную работу, то цикл может быть пущен и в обратную сторону. Понятие о такой обращенной тепловой машине тоже введено С. Карно в его знаменитой книге. При таком «обращении» идеального цикла все количественные соотношения между величинами, определяющими его работу, останутся прежними, только вместо переноса «теплорода» с высокой температуры на низкую будет происходить обратный процесс — перенос его с низкого уровня температуры на высокий. Для этого потребуется ровно столько же работы, сколько ее было получено, и все вернется в исходное состояние. Другими словами, такой цикл обладает свойством обратимости. На рис. 3.2 показаны оба случая с потоками энергии. Потоки энергии показаны в виде полос, ширина которых пропорциональна потоку энергии. Такие графики называются полосовыми. Отношения Q/T в
Примечательно, что сам С. Карно в определенной степени это чувствовал: везде, где он говорил о теплоте (в смысле величины Q), использовалось слово chaleur (тепло), а где о теплороде — другое, уже упоминавшееся нами слово calorique — теплород. То, что это не случайность, видно из того, что такая терминология ни разу не нарушается.
Обоих случаях остаются одинаковыми и на входе теплоты, и на ее выходе.
Таким образом, тепловой двигатель превратится в «тепловой насос», перекачивающий «теплород» с низкой температуры на высокую с затратой работы. Поток приведенной теплоты подобно потоку «теплорода» и здесь пройдет неизменным через машину, но не «сверху вниз», как в двигателе, а «снизу вверх», как в насосе. Если бы заснять действие машины на кинопленку, то ее (и машину, и пленку) можно было бы крутить в любом направлении: картина была бы верной во всех случаях.
|
А)
Рис. 3.2. Полосовые графики потоков энергии и энтропии: а — тепловой двигатель; б — тепловой насос |
Это замечательное свойство величины Q/T оставаться неизменной при всех идеальных (и, следовательно, обратимых) взаимных превращениях теплоты и работы не могло не обратить на себя внимания.
Р. Клаузиус (1822-1888 гг.) был первым, кто придал величине Q/T самостоятельное значение и ввел ее в науку. Он назвал ее энтропией[28]. С тех пор (1865 г.) энтропия (ее по стандарту обозначают буквой S) начала свой славный и вместе с тем тернистый путь в науке. Славный потому, что она «работала» и продолжает «работать», помогая решать множество важнейших теоретических и практических проблем (и не только термодинамических). Тернистый потому, что трудно найти другое научное понятие, вокруг которого кипели бы такие страсти и которое вызвало бы столько кривотолков, ошибок и нападок. Достается ей и от идеологов, и от изобретателей ррш-2.
В чем тут дело, станет окончательно ясным, если рассмотреть некоторые свойства энтропии.
Начнем с того, что энтропия имеет еще одно важное свойство, роднящее ее с «теплородом». Она может не только подводиться к телу вместе с теплотой (или отводиться от него), но и, в отличие от теплоты, накапливаться в теле, «содержаться» в нем. При работе двигателя Карно или теплового насоса энтропия, как мы видели, «протекает» через них (рис. 3.2). Сколько ее входит, столько и выходит. Но при нагреве вещества путем подвода к нему теплоты энтропия поступает, но не выходит: она «накапливается» в веществе. Теплота исчезает, превращаясь во внутреннюю энергию, а энтропия увеличивается. Напротив, при отводе теплоты энтропия тела убывает. Таким образом, энтропия может как содержаться в телах, так и посредством теплоты передаваться от одного тела к другому.
Соотношением S = Q/T можно пользоваться тогда, когда все количество теплоты Q отдается при одной и той же температуре Т. На практике температура Т в процессе подвода теплоты большей частью меняется, так как тело нагревается (а при отводе охлаждается). Дня каждой малой порции теплоты 5Q температура будет уже другой; поэтому энтропию подсчитывают для каждой порции теплоты отдельно в виде 5S = 5Q/T и потом суммируют порции энтропии SS. В целом количество энтропии AS будет равно сумме малых изменений величины 5S; AS = Y1 а ПРИ переходе к бесконечно малым
A s = jf. (3.4)
Ті
Из соотношения SS = 6Q/T следует, что поток теплоты можно представить как произведение температуры Г, при которой она передается, на поток энтропии:
8Q = T5S. (3.5)
Эта формула имеет глубокий физический смысл. Обратим внимание на то, что при передаче энергии в форме механической работы ее количество, как и по формуле (3.5), тоже определяется произведением двух аналогичных величин.
Возьмем два примера — по одному для каждого случая (рис. 3.3): работу сжатия газа в цилиндре (а) и нагрев
Газа в теплоизолированном сосуде (б). В первом случае работа I равна произведению силы Р (равной произведению давления р на площадь поршня F) на путь Sh (равный отношению изменения объема SV к площади поршня F). Так как по мере сжатия газа сила Р должна расти, работу надо считать по малым отрезкам Sh, на которых ее можно принимать постоянной. Тогда работа будет составлять произведение двух величин:
SI = pSV. (3.6)
Нетрудно видеть, что во втором случае, аналогично первому, для некоторого элементарного количества теплоты SQ, при передаче которого Т неизменна,
Sq = TSS. (3.7)
Таким образом, передача энергии в двух формах — теплоты и работы (несмотря на их принципиальную разницу — неорганизованную форму в первом случае и организованную во втором) может быть выражена аналогично. Количество энергии в обоих случаях (3.6) и (3.7) выражается произведением двух величин.
Первая из них (давление р для работы и температура Т для теплоты) — это силы (потенциалы), которые вызывают данную форму передачи энергии. Вторая — это «так называемые координаты, изменение которых показывает наличие данной формы передачи энергии. Если координата (V или S) не изменилась (т. е. SV или SS равны нулю), то SL и SQ тоже будут равны нулю и никакой передачи энергии не произойдет.
|
81 = pbh 4 |
|
А) б) Рис. 3.3. Передача энергии в форме работы 81 и теплоты Sq |
Первые величины называют еще факторами интенсивности, а вторые — экстенсивности. Следовательно, энтропия — фактор экстенсивности при передаче энергии в форме теплоты. Интенсивные факторы не связаны с массой тела, которому передается энергия, экстенсивные факторы, напротив, зависят от нее: и энтропия S, и объем V
при прочих равных условиях тем больше, чем больше масса газа. Соответственно они измеряются в единицах, отнесенных к единице массы.
Понятие об интенсивных и экстенсивных факторах имеет очень широкий смысл, далеко выходящий за пределы термодинамики. Интенсификация любого процесса (даже в народнохозяйственном плане) достигается не за счет увеличения экстенсивного фактора, а только посредством интенсивного фактора. В случае передачи энергии в форме теплоты таким фактором служит температура.
Может возникнуть естественный вопрос: если изменение энтропии, равное нулю, показывает отсутствие передачи энергии в форме теплоты, то как быть с тепловой машиной Карно? Ведь к ней теплота и подводится, и отводится, а энтропия постоянна?
Это противоречие кажущееся: внешние потоки энтропии постоянны, но внутри машины циркулирующее рабочее тело постоянно и нагревается, и охлаждается. При его нагревании двигатель получает теплоту и энтропия рабочего тела растет; при охлаждении и отводе теплоты энтропия уменьшается. В идеальном процессе эти величины равны, и в целом энтропия непрерывно отдается теплопри - емнику в том же количестве, что и поступает от источника теплоты. Поэтому круговой процесс — цикл может повторяться сколь угодно долго.
Закономерность, характерную для идеальных процессов, — существование величины S, которая в сумме не меняется во всех процессах, связанных с переносом энергии, — можно назвать принципом существования и постоянства энтропии.
Если бы свойства энтропии ограничивались только постоянством в идеальных обратимых процессах, то споров вокруг нее было бы значительно меньше. Однако энтропия имеет еще одно важное свойство, именно оно уже более 100 лет вызывает острые споры.
Начало им положил тот же Р. Клаузиус. Он развил идеи С. Карно на новом уровне, основанном на механической теории теплоты, и установил еще одно важное свойство энтропии. Опираясь на него, Клаузиус делает один далеко идущий вывод, из-за которого и возникла дискуссия, продолжавшаяся больше века.
О чем же идет речь?
С. Карно ввел и рассматривал идеальные обратимые процессы, в которых переход теплоты от тела с высокой температурой Т — теплоотдатчика — к телу с низкой температурой Т2 — теплоприемнику — сопровождается полу
чением работы; напротив, переход теплоты от теплоотдат - чика с низкой температурой Т^ к теплоприемнику с более высокой температурой Т происходит с затратой работы.
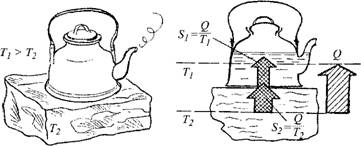
Однако существуют и другие, необратимые процессы переноса теплоты, могущие сами по себе идти только в одну сторону. Именно на них и обратил внимание Клаузиус. Действительно, что будет, если источник теплоты — теплоотдатчик с более высокой температурой Т — привести в тепловой контакт (например, соединить металлическим стержнем) с теплоприемником, температура Т2 которого ниже, без тепловой машины? Тогда возникнет тепловой поток от тела с температурой Т к телу с температурой Т2; работы при этом, естественно, никакой не производится, и всю теплоту, отдаваемую теплоотдатчиком, получит теплоприемник.
Таким образом, процесс в этом случае будет односторонним, необратимым, поскольку в обратную сторону он идти не может. (Горячая печка может греть холодный чайник, но холодный чайник греть горячую печку не может.) Как будет вести себя здесь энтропия? Теплоотдатчик отдает энтропию Si = Q1/T1; тепло - приемник получает энтропию S2 = Qi/T2 (теплота, получаемая тепло - приемником Q2 = Qі, так как она на работу не расходуется). Поскольку Г2 < Гь то S2 > S±. Энтропия возрастает!
Тот же эффект может получиться и при работе тепловой машины, но не идеальной, как у Карно, а реальної% действие которой сопровождается потерями.
|
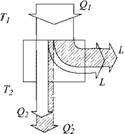
Рис. 3.4. Полосовые графики потоков энергии в тепловом двигателе при обратимом и необратимом протекании процессов |
Для реального двигателя это означает, что при тех же температурах Т и Т2 (рис. 3.4) и количестве теплоты Qi работа будет уже не L, a L! < L. Следовательно, по закону сохранения энергии теплоприемник получит уже большее количество теплоты Q!2 > Q2, так как в работу ее перешло меньше: Q2 — Qi — L, Q!2 = Qi — L' но L! < L, следовательно, Q2 > Qi - Отсюда следует, что полученная теплоприемником энтропия s'2 = Q2/T2 > S,2-
Опять энтропия возросла!
Для реального теплового насоса при тех же температурах Т и Т2 и том же количестве теплоты Q2 затрата работы L' будет больше, чем в идеальном случае: L' > L. Поэтому количество теплоты Q[ будет также больше, чем Qi, так как Q[ = Q2 + L!. Следовательно, энтропия, получаемая теплоприемником при Ті, будет больше, чем при работе идеального теплового насоса:
С/ Qi. с Qі
И здесь энтропия возрастает! Анализ и других реальных необратимых процессов преобразования энергии неукоснительно показывает — энтропия в них, возрастает.
Р. Клаузиус обобщил эту закономерность на любые необратимые энергетические процессы, введя принцип возрастания энтропии: во всех реальных процессах преобразования энергии в изолированных системах[29] суммарная энтропия всех участвующих в них тел возрастает. Это возрастание энтропии при прочих равных условиях тем больше, чем сильнее процесс (пли процессы) в рассматриваемой системе отличается от идеальных, обратимых. В тепловом двигателе, например, как мы видели, ухудшение его действия (т. е. уменьшение получаемой из того же количества теплоты Q работы L при тех же граничных температурах Т и Т2) обязательно сопровождается увеличением энтропии. В тепловом насосе увеличение необходимых затрат работы приводит к тому же результату — росту энтропии. Следовательно, энтропия может выполнять еще одну «должность» — быть характеристикой необратимости процессов, показывать отклонение их от идеальных. Чем больше рост энтропии, тем это отклонение больше.
Таким образом, второй закон термодинамики состоит из констатации двух положений — существования и постоянства энтропии в обратимых процессах (Карно) и возрастания энтропии в необратимых процессах (Клаузиус).
Уменьшение энтропии в изолированных системах второй закон запрещает: оно в принципе невозможно: Примеров таких воображаемых невозможных процессов можно привести много: это самопроизвольный переход теплоты от холодного тела с температурой Т^ к более теплому с температурой Ті > Г2, например, закипание чайника с водой, поставленного на лед (или замерзание в жару воды в водопроводной трубе). Нетрудно видеть (рис. 3.5), что энтропия при этом уменьшалась бы, поскольку энтропия S воды в чайнике возрастала бы на Q/T, а энтропия S льда уменьшалась на Q/T2. Двигатель, работающий на «концентрации тепловой энергии, отводимой из окружающего пространства» (т. е. производящий работу или электроэнергию из внутренней энергии равновесной окружающей среды)[30], относился бы к этой же группе нереализуемых систем. Действительно, получая некоторое количество теплоты Qo c от среды при ее температуре Го с (а с ней неизбежно и соответствующую энтропию S = Qo. c/Tq. c5 он выдавал бы некоторую работу, в которой энтропии нет. К чему это привело бы?
|
Рис. 3.5. Чайник, кипящий вопреки второму закону термодинамики, но в согласии с первым законом |
Если бы вся теплота Q0.с превратилась в работу, то энтропия исчезла бы совсем. Если же в работу L превратилась бы только часть теплоты Qo c, а остальную ее часть Q2 двигатель отдал бы обратно, то все равно отданная энтропия была бы меньше, чем полученная так как Q2 < Q0.с И S2 = Q2/Tq, c < Qo. c/To. c-
Чтобы завершить знакомство с энтропией, остается затронуть еще один аспект этой замечательной величины — ее статистическую трактовку. Она была дана двумя великими физиками — Л. Больцманом (1844-1906 гг.) и М. Планком (1858-1947 гг.).
Они подошли к понятию энтропии с другой стороны, так сказать, «изнутри», от молекулярного строения материи. Больцман исследовал законы поведения всего множества молекул, составляющих взаимодействующие части системы, и установил, что существует непосредственная связь энтропии с тем состоянием, в котором эти молекулы находятся.
Каждая молекула обладает в каждый определенный момент определенной энергией, связанной с ее движением и взаимодействием с другими молекулами. Общая внутренняя энергия вещества представляет собой сумму энергий этих частиц. Поскольку молекулы постоянно находятся в хаотическом движении и взаимодействуют между собой, между ними происходит энергетический обмен, приводящий к тому, что энергия все время перераспределяется между ними. Поэтому каждый следующий момент соответствует уже другому микросостоянию системы с другим распределением энергии между молекулами.
Таким образом, микросостояние системы — это такое ее состояние в данный момент, при котором для каждой молекулы определены положение в пространстве и скорость. Это, если так можно выразиться, мгновенный снимок системы.
Изучить в такой ситуации хаоса и беспорядка, существующей в каждом микросостоянии, поведение каждой молекулы, чтобы предсказать ее поведение в дальнейшем, практически невозможно. Но это и не нужно: достаточно знать возможные варианты общего поведения системы, т. е. число всех ее возможных микросостояний.
Число w таких микросостояний может быть очень велико, огромно, но оно все же не бесконечно, так как число молекул конечно, как и число энергетических уровней, на которых они могут находиться.
Но каково же будет состояние системы, определяемое общими характеристиками (плотность, энергия и т. д.), т. е. ее макросостояние в данных условиях? Какое из многочисленных микросостояний она «выберет»? Оказывается, зная число и особенности различных возможных микросостояний, можно установить ее наиболее вероятное макросостояние. Этот закон будет статистическим, что, однако, ничуть не снижает его силы и надежности.
Чтобы показать, на чем он основан, используем наглядный пример, приведенный чл.-корр. АН СССР JI. M. Би - берманом.
Пусть на плоском подносе расположены несколько одинаковых монет. Каждая из них может лежать только в одном из двух положений — гербом вверх («орел») или вниз («решка»). Поскольку оба положения совершенно равновероятны, каждая монета может лечь вверх орлом или решкой; заранее предсказать это невозможно.
Движением подноса можно одновременно подбросить все монеты. Допустим, что вначале они все лежали в строгом порядке — орлом вверх. Поставим вначале вопрос так: можно ли путем последовательных подбрасываний монет на подносе (при которых все они, естественно, будут переворачиваться по-разному) вернуться к исходному положению? В принципе, разумеется, можно. Но сколько нужно для этого подбрасываний? Попробуем определить их число, например, для 10 монет. В этом случае возможны разные варианты («микросостояния»): все десять монет гербом вверх (10|), девять вверх — одна вниз (9|, Ц), восемь вверх — две вниз (8|, 2[) и т. д. до одиннадцатого — все вниз (Ю|). Этот последний вариант (10|) тоже соответствует полному порядку, только обратному первому
Все эти варианты на первый взгляд равноправны, равновероятны, но это только на первый взгляд. На самом деле они резко различаются тем, что частота их появления будет неодинакова. Действительно, первый вариант можно реализовать только одним способом, а второй — уже десятью (первая монета орел, остальные — решка; вторая — орел, остальные — решка; третья — орел, остальные — решка и т. д.). Следовательно, второй вариант будет возникать в 10 раз чаще первого. Третий вариант (8|, 2[) можно реализовать еще намного большим количеством способов. Действительно, двумя монетами, повернутыми вниз, могут быть первая и вторая, первая и третья (и т. д.), вторая и третья, вторая и четвертая и т. д. Легко убедиться, что таких способов будет уже 45. Четвертый вариант реализуется уже 120 способами.
Если свести все данные вместе, то получим такую таблицу:
|
Расположение |
Ют |
9Т |
8| |
7| |
6Т |
5Т |
4Т |
Зт |
2| |
It |
От |
|
Монет (макро |
0| |
Ц |
21 |
31 |
4| |
51 |
6| |
П |
81 |
91 |
101 |
|
Состояния) |
|||||||||||
|
Число способов |
1 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
|
Реализации |
|||||||||||
|
(микросостояний) |
Всего, следовательно, в сумме возможны Но; = 1024 микросостояния. Из них состояния «полного порядка» (0 j, 10| и 10|, 0|) встречаются только по 1 разу. Напротив, наиболее далекие от порядка микросостояния (5|, 5|), 6|), (6|, 4|) встречаются наиболее часто; чаще всего (5 j, 5|) — 252 раза.
Таким образом, для получения первоначального порядка нужно встряхнуть поднос не менее 1024 раз! Напротив, перемешать все поровну можно за каких-то (1024/252) четыре встряхивания. Микросостояние полного перемешивания в 252 раза вероятнее, чем состояние полной упорядоченности. Путь от порядка к беспорядку очень короток, но чтобы пройти путь от беспорядка к порядку, нужно поработать намного больше! Здесь мы встречаемся с понятием термодинамической вероятности w, которая определяется числом тех микросостояний, которыми может быть реализовано данное макросостояние. Понятие термодинамической вероятности отличается от понятия математической вероятности случайного события, которая определяется отношением числа появлений данного события к общему числу испытаний. В данном случае математическая вероятность определялась бы для каждого случая величиной w/YtW.
В описанном эксперименте мы взяли всего 10 монет. А если их будет больше?
Ниже даны суммарные округленные цифры Yw микросостояний для числа монет п до 100:
П................................... 10 20 30 50 70 100
Yw................................ 103 106 109 1015 1021 Ю30
Это означает, что для возвращения к упорядоченному расположению монет при их числе, например 100, нужно время, большее времени существования солнечной системы1 — (7 8) • 109 лет.
^сли встряхивать поднос 1 раз в секунду.
Pi < Pi Но ведь молекул газа в са
Мом малом объеме несоизмеримо больше, чем 100 (при давлении 0,1 МПа и температуре 273 К — около 3 х 109 в 1 см3). Поэтому термодинамическая вероятность w того, что молекулы равномерно распределятся в любом свободном объеме беспорядочно с мгновенными скоростями, направленными хаотично, чрезвычайно велика; этому соответствует гигантское количество возможных микросостояний YtW. Напротив, по сравнению с этим вероятность установления микросостояний, в которых будет определенный порядок, совершенно ничтожна. Практически она равна нулю.
Рассмотрим три таких упорядоченных состояния.
1. В одной половине сосуда собралось вдвое больше молекул, чем в другой. Соответственно давление рі в одной половине будет в 2 раза больше, чем р2 в другой — (р2 = 2pi). Эта ситуация схематично показана на рис. 3.6, а.
2. В одной половине сосуда собрались те молекулы, у которых средняя скорость теплового движения больше, а в другой — те, у которых она меньше некоторого заданного значения. (Известно, что в газе имеются молекулы с разными скоростями; его температура определяется их средним значением.) Тогда газ в одной половине сосуда будет горячим (с температурой Ті), а в другой — холодным (с температурой Т2 < Т. Такая ситуация изображена на рис. 3.6, б; в принципе она аналогична случаю с чайником, показанному на рис. 3.5.
|
Рис. 3.6. Примеры взаимных переходов упорядоченных и неупорядоченных состояний: а — разность давлений (р2 > р) б — разность температур (Т2 < Ті); в — разность концентраций (С2 > Сі) |
3. В сосуде, где находится смесь двух газов (например, воздух, состоящий из кислорода и азота), молекулы одного газа (кислорода) соберутся преимущественно в одной ча
сти сосуда, а второго газа (азота) — в другой: В сосуде возникнет разность концентраций с и С2, (рис. 3.6, в).
И теория, и опыт показывают, что такая ситуация — самопроизвольное упорядочение — возникновение разностей давлений р, температур Т или концентраций с столь маловероятна, что ее возникновение было бы чудом. Напротив, если такую разность создать искусственно, путем внешнего воздействия (с затратой соответствующей работы), она тут же начнет самопроизвольно выравниваться.
Действительно, если разделить сосуд перегородкой и заполнить его отсеки кислородом и азотом, то при удалении перегородки газы равномерно перемешаются. То же будет при разных давлениях или температурах — они выравня - ются, и в конце концов установится некоторое среднее значение.
Теперь мы можем вернуться к свойствам энтропии — статистической трактовке. В результате работ JL Больцмана и затем М. Планка была установлена известная зависимость
S = klnw.1 (3.8)
Энтропия пропорциональна логарифму термодинамической вероятности (т. е. числу w микросостояний, которыми данное макросостояние может быть реализовано). Коэффициент к — постоянная Больцмана — имеет определенный физический смысл: он равен отношению универсальной газовой постоянной Rм к числу Авогадро Na-
Применительно к примерам, рассмотренным выше, формула (3.8) показывает, что чем больше число w (например, все монеты лежат в беспорядке или газ равномерно распределен в сосуде и т. д.), т. е. чем больше вероятность данного состояния, тем больше и энтропия S. Если, напротив, w —> 1, т. е. все единственным образом упорядочено (например, все монеты лежат одинаково), то S = О (поскольку In 1 = 0).
Таким образом, поскольку все физические системы самопроизвольно стремятся к состоянию большей вероятности, к равновесию, то энтропия любой изолированной системы, свободно меняющей свое состояние, может только увеличиваться. Если система уже находится в равновесии или обратимо изменяет состояние, то энтропия будет постоянной. Самопроизвольно она уменьшаться не может.
!Эта формула высечена на пьедестале надгробного памятника Больц - ману в Вене.
Все три процесса, показанные на рис. 3.6, могут идти только влево (рост энтропии S). Вправо (штриховая стрелка) они идти не могут, так как энтропия при этом уменьшилась бы, что невозможно.
Таким образом, и статистическая трактовка энтропии приводит тоже к положениям второго закона термодинамики: в изолированных системах энтропия может либо оставаться неизменной (в идеальных, обратимых процессах, где уровень неорганизованности остается неизменным), либо возрастать (в реальных процессах, где неупорядоченность, неорганизованность возрастают).
В формулировке М. Планка эта мысль выражена предельно четко: «В природе для каждой системы тел существует величина, которая при всех изменениях, которые затрагивают только эту систему, или остается постоянной (обратимые процессы), или увеличивается (необратимые процессы). Это энтропия системы».
Эта формулировка второго закона термодинамики очень близка по стилю и четкости к формулировке первого закона, которую дал Фейн - ман (мы ее приводили на с. 86) и смысл которой аналогичен утверждению: «Существует величина, которая при всех изменениях, которые затрагивают только эту систему, остается постоянной. Это энергия системы».
Соответственно существование ррш-1 противоречит постоянству энергии, существование ррш-2 точно так же противоречит постоянству или возрастанию энтропии.
В отличие от первого закона, относящегося к так называемым «динамическим», второй закон носит, как мы видели, статистический характер. В «рассуждении» о законах, которым заканчивалась предыдущая глава, мы обещали вернуться к статистическим законам позже. Сейчас это можно сделать.
Динамические законы описывают состояние и поведение индивидуальных объектов (тел, систем). Внутреннее их строение для динамических законов не имеет значения. Если известно, что система А передала системе В какое-то количество энергии W (в условиях, когда они обе изолированы), то мы точно знаем, что энергия системы А уменьшилась точно на W, а системы В ровно на столько же увеличилась, совершенно независимо от того, что в них при этом происходило.
Статистические законы описывают состояние и поведение совокупности (множества) объектов, рассматривая ее как нечто целое.
При таком подходе физическое тело (например, газ) рассматривается как множество молекул, поведение каждой из которых определяется случайностью. Мы не можем точно сказать, как ведет себя каждая молекула в отдельности (как, например, каждая монета в рассмотренном выше примере). Однако «общее поведение» молекул (так же как и число монет, находящихся в определенном положении) мы найти с определенной степенью вероятности можем. Эта вероятность, как мы видели, тем больше, чем больше число отдельных молекул определяет давление, температуру и энтропию газа или жидкости.
Вероятность верного предсказания таких общих величин, определяемых статистическими законами, как мы видели даже на простых примерах, практически равна единице, а отклонения от нее — нулю1.
После появления первых статистических законов они сначала считались «второстепенными», «неполноценными». Сейчас статистические законы заняли в науке, в частности в физике, равноправное (если не преобладающее) положение по отношению к динамическим. Они столь же надежно предсказывают поведение систем (естественно, если количество частиц, входящих в множество, достаточно велико), как и динамические.
Поэтому второй закон термодинамики, имеющий статистическую природу, столь же надежен и «непробиваем», как и первый.
Попытки обосновать ррт-2, ссылаясь на «неполноценность» второго закона из-за его статистической природы, абсолютно безнадежны.
Пользуясь понятием энтропии, мы можем четко определить, какие процессы в принципе допускаются вторым законом термодинамики и какие он не разрешает. Очевидно, что к первым относятся все те, где энтропия S неизменна или возрастает, а ко вторым — те, где она уменьшается.
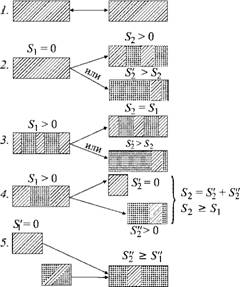
Удобнее всего показать это графически (рис. 3.7). Слева условно в виде прямоугольников изображены исходные состояния (до проведения процесса), справа — конечные (после его завершения). Размеры каждого прямоугольника, показывающего состояние системы, соответствуют ее энергии; по закону сохранения энергии их площадь в конечном состоянии равна начальной. Чем меньше энтропия S системы, тем более эта система упорядочена. Линиями со стрелками на рисунке показано возможное направление
Иногда возникает вопрос о том, как в природе осуществляется переход к более вероятным состояниям. В примере с монетами и подносом для этого потребовалась некая «внешняя сила» — нужно было кому - то трясти поднос. А в природе? Дело в том, что природа сама всегда «трясет поднос», поскольку неподвижности, равновесия в ней нет. Другое дело, что иногда (и даже часто) эта «тряска» не настолько сильна, чтобы быстро «растормозить» некоторые неравновесности.
Человек в своих интересах может этот процесс ускорить. Например, сжигая топливо для получения электроэнергии, мы используем химическую неравновесность между топливом и кислородом воздуха, подробнее об этом будет сказано дальше.
Протекания процессов; переход в обратном направлении невозможен.
Sx = 0 52 = 0
|
S'{> 0 Рис. 3.7. Возможные переходы систем из одного состояния в другое. Переход слева направо возможен во всех случаях, справа налево — только в первом (процесс обратим) |
Первый процесс — переход из одного полностью организованного состояния 7), соответствующего нулевой энтропии (обозначено штриховкой), в столь же упорядоченное состояние (2). Характерными примерами устройств с такими процессами могут служить механический редуктор, электрический трансформатор или двигатель. В предельном случае каждый из них может полностью преобразовать механическую работу или электроэнергию в работу или электроэнергию с другими, нужными характеристиками. Если же в системе будут потери (трение, тепловыделения от электронагрева), то переход системы в новое состояние будет сопровождаться некоторым возникновением энтропии (случай 2). Чем больше потери, тем больше будет ее значение (Sf2 > S2> Si = 0).
Может быть и так, что система в исходном состоянии характеризуется некоторой энтропией Si, отличной от нуля (случай 3). Она может перейти как в состояние с такой же энтропией S2 = Si, сохранив исходный уровень неупорядоченности (идеальный процесс), так и в любое состояние с большей энтропией S'2 > S2 (реальный процесс).
Может быть и так (случай 4), что из одной системы образуются две (или из одного потока энергии два). Тогда полученная сумма энтропии должна либо быть равной исходной (идеальный процесс, S'2 + S'^ = Si), либо превышать ее (реальный процесс, Sf2 + S'^ > Si). В этом последнем случае возможна, в частности, и ситуация, при которой один из конечных результатов процесса (часть системы или поток энергии) будет характеризоваться меньшей энтропией, чем исходное состояние. Но такое «облагораживание» (уменьшение беспорядка) в одной части неизбежно компенсируется равным или еще большим ростом энтропии в другой части. Здесь одна часть «выбивается в упорядоченные» за счет другой части, но в конечном результате общая энтропия опять вырастет.
Наконец, пятый случай. Здесь вначале либо имеются две системы с разной энтропией, либо подводятся два потока энергии: один в упорядоченной форме (S[ = 0, работа), а другой — в неупорядоченной (S'{ > 0, теплота). В результате получается система (или поток энергии) с общей энтропией S'2, большей (в реальном процессе) или равной (в идеальном) энтропии S"1.
Нетрудно видеть, что все технические устройства, созданные человеком, преобразуют энергию по одной из описанных схем (или их сочетаниям). О первой и второй мы уже говорили. Третья соответствует многочисленному классу процессов, в которых перерабатываются потоки разного уровня неупорядоченности без существенного участия безэнтропийных, упорядоченных потоков энергии (работы, электроэнергии). К ним относятся многие химико - технологические процессы и другие, в которых участвуют в основном потоки вещества и теплоты.
Очевидно, что в четвертом и пятом случаях справа (и соответственно слева) могут быть не две системы или два потока, а больше. При этом условие, что суммарная энтропия справа должна быть равной или большей энтропии слева, естественно, сохраняется.
Примером четвертого случая может служить тепловая электростанция, вырабатывающая электроэнергию (S = 0) и отдающая непревращенную теплоту с большей энтропией в окружающую среду.
Наконец, пятому случаю соответствует тепловой насос. К системе подводится работа (S[ = 0) и теплота из окружающей среды S'{ > 0, а отводится теплота при более высокой температуре с энтропией > S'[. Все случаи преобразования энергии, в которых превращение по схемам 2-5 шло бы не слева направо, а справа налево, относятся к нереализуемым: они невозможны, поскольку энтропия уменьшается. Все вечные двигатели второго рода, которые мы будем рассматривать в дальнейшем, сводятся в конечном счете к одной из этих невозможностей.
Все сказанное в этой главе о принципе Карно, порядке и беспорядке, об энтропии и ее статистической трактовке показывает, что второй закон термодинамики, запрещающий ррш-2, нельзя опрокинуть доводом о том, что он «не всеобщий, поскольку статистический». Всюду, где действуют физические законы статистической природы (а все возможные, вернее, невозможные варианты ррш-2, как и вся техника, действуют именно в этих условиях), второй закон незыблем. Житейское правило (особенно хорошо известное женщинам), что беспорядок из порядка всегда возникает сам по себе, а наведение порядка всегда требует затраты работы, здесь оправдывается в полной мере.
Однако в запасе у идеологов ррш-2 есть еще три «мощных» довода против второго закона. Один из них связан с философско-космологическими проблемами — это опровержение теории «тепловой смерти Вселенной». Опровергая эту теорию, сторонники ррш-2 пытаются низвергнуть и второй закон. Другой довод — это существование жизни, которая, по их мнению, тоже опровергает второй закон.
Третий довод далеко не такой глобальный, как первые два: он относится к области техники. Сторонники ррш-2 считают, что уже существует техническое устройство, действие которого наглядно опровергает второй закон термодинамики. Это, как ни странно, — тепловой насос, о котором мы уже упоминали. Поэтому нельзя перейти к разбору конкретных образцов ррш-2 без того, чтобы не коснуться как первых двух, казалось бы, далеких от энергетики вопросов, так и третьего, прямо к ней относящегося, — о тепловом насосе.