ТЕХНОЛОГИЯ ОГНЕУПОРОВ

ТЕРМОСТОЙКОСТЬ

Способность огнеупоров противостоять, не разрушаясь, колеба­ниям температуры при нагревании или охлаждении называют термо­стойкостью. По ориентировочной оценке 4$ огнеупоров разрушается
вследствие недостаточной их термостойкости при температурах, зна­чительно более низких, чем огнеупорность (плавление). В основе яв­лений, вызывающих термическое разрушение, лежат процессы, свя­занные с возникновением в материале напряжений. Термические на­пряжения бывают двух видов: напряжения I рода, вызываемые градиентом температур, и напряжения II, вызываемые анизотропией термического коэффициента линейного расширения, химическими ре­акциями, расширением при полиморфизме. Эти напряжения возни­кают при постоянной температуре, их называют также химическими. В обоих случаях напряжения возникают тогда, когда материал не имеет возможности свободно изменять свой объем по тем или иным причинам. Наиболее подробно изучена термостойкость при напряже­ниях I рода.

Напряжения I рода

При нагревании тела с поверхности внешние (поверхностные) слои его нагреваются и расширяются быстрее, чем внутренние. На­пряжения, возникающие из-за препятствия изменению размеров, яв­ляются сжимающими, посколь­ку тело стремится расширить­ся. При охлаждении возника­ют растягивающие напряже­ния. Величина напряжений прямо пропорциональна терми­ческому коэффициенту линей­ного расширения, модулю уп­ругости, перепаду температур (Тср—Т) и обратно пропор­циональна (1—ц) по формуле (II.39). Значения напряжений, как было показано, могут пре­восходить прочность материа­ла.

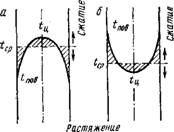
Эпюры напряжений в пластинке при нагревании и охлаждении изображены на рис. 11.12. При изменении температуры с постоянной скоростью распределение ее внутри тела будет параболическим. Для огнеупоров предел прочности при сжатии больше, чем при растяже­нии, поэтому при нагревании огнеупорных изделий деформация в виде трещин возможна в центре, а при охлаждении — на поверх­ности.

В формуле (11.39) для напряжений на поверхности и в центре перепад температур будет соответственно равен Гпоя) и

('ср—7"„). Определить температуру непосредственно на поверхности и В центре сложно.

Значения температур в центре и на поверхности зависят от'теп­лопередачи от поверхности к окружающей среде К, теплопровод­ности материала X и расстояния между поверхностью и центром rjn, т. е. от половины толщины тела. Эта зависимость выражается безразмерным критерием Био:

Р = гт/СД. (Ц.46)

Таким образом, напряжения I рода зависят от свойств материа­ла (а, а, Е, ц, х), формы изделий, размеров (rm), условий теплопе­редачи (р), скорости изменения температур и др.

Теория термостойкости хрупких тел при развитии '

В них максимальных напряжений

По теории максимальных напряжений тело разрушается, когда его прочность меньше образующихся в нем максимальных термиче­ских напряжений. По первому способу термостойкость выражается в критериальной форме отношением, прочности к напряжению:

R = an4(l-n)l(Ea), (11.47)"

Где R— критерий термостойкости; чем больше его значение, тем вы-' ше термостойкость; оПч — прочность материала, кПа (это может, быть предел прочности при изгибе, растяжении или при сжатии); Е — модуль упругости, кПа; а — термический коэффициент линейно­го расширения, К-1; р— коэффициент Пуассона; значение р. бе­рется с целью исключения поперечных напряжений.

Поскольку абсолютное значение R зависит от выбора величины 0пч, сравнение термостойкости различных материалов правомерно при одинаковом характере прочности. Все величины в формуле (11.47) берутся при комнатной температуре; при этом изменение зна­чений [г и а от температуры ввиду незначительности изменений не учитывается, а изменение значений Ого-го «Оізоо/^ізоо-

Распространение температуры в теле зависит от теплопроводно­сти и температуропроводности, критерии термостойкости с учетом % и а имеют вид;

Rl=RM (11.48)

Ru = Rat (11.49)

R, R1 и Ru принято называть соответственно критерием термо­стойкости, I критерием термостойкости и II критерием термостой­кости.

Применение того или иного критерия определяется значением критерия Био: R применяют при критерии Био>20, т. е. при высо­ких скоростях теплопередачи от поверхности в окружающую среду; R1 — при критерии Био<2, т. е. при низких скоростях теплоотдачи; R11 — при постоянной скорости изменения температуры. Применени­ем трех критериев термостойкости в некоторой степени учитываются условия теплопередачи, но, как будет показано ниже, не полностью.

Второй способ выражения критерия термостойкости заключается в следующем. Для пластины термическое напряжение, как было по­казано в формуле (11.39), выражается уравнением

О„ = аг = 1Еа/(1—ц)ЦТср — Г), (II. 49а)

Где аи=сх — прочность материала по-оси у или г, откуда

(Т'ср — Т) = ЛТр — ■ (Н.50)

Т. е. критерий термостойкости R равен перепаду температур, при ко­тором разрушается тело, R = ATp. Для другого тела, по форме отли­чающегося от пластины:

ДГР=[0ПЧ(1 -|i)/(Јa)]S' = RS', (И.51)

Где У — фактор, зависящий от формы. 38

Термостойкость с учетом критерия Био ft, по Киигери, выража­ется формулами:

ЛГР = [апч (I - Ц)/(£«)] S' 1 /0,Зір (IIі52)

Или ■

АТрг= Л1 S [1/(0,31rm /Qh (IIі53)

Из последних формул следует, что нельзя составить таблицу термостойкости материалов в порядке ее повышения, так как термо­стойкость не определяется однозначно свойствами материала, а за­висит также от формы, размеров и коэффициента теплопередачи. Иначе говоря, термостойкость не является физическим свойством ма­териала.

При высоких температурах с появлением в огнеупорах жидкой фазы или в результате ползучести материал находится в упруго-вяз­ком и упруго-пластическом состояниях. Термостойкость при этом по­вышается:

/?крип — Rynp ~h Кэл, (II .54)

Где Ryav — упругий критерий термостойкости, определяемый по фор­мулам (11.47—11.53); Ran — эластичный критерий термостойкости:

Яэл = Кч (1 - {і) /(сиікаж)] 5', (II .55)

Где г)Каж — коэффициент кажущейся вязкости, отражающий способ­ность материала релаксировать (замедлять) действие термических напряжений при длительном их воздействии.

Вопрос о вязкости аморфно-кристаллического тела, находящего­ся в термопластичном состоянии, является сложным. Кажущаяся вязкость может быть определена экспериментально при испытании огнеупоров на изгиб по формуле Соломина:

%аж = от (I - до K3SM), (И. 56)

Где а—нагрузка, Па; г — время ползучести, с; S, / — начальные зна­чения сечения, см2, и длины образца, м; Ы — изменение длины за вре­мя т, с.

Кажущаяся вязкость определяется по формуле Орловой: %аж = НкО'тв/Уж), (Н.57)

Где і]ж ~ вязкость расплава, образующегося в огнеупоре; FTb, Vm — объемные доли соответственно твердой и жидкой фаз (определяются под микроскопом); k — коэффициент структуры (для шамотных из­делий с 39% А1203 &=3,7-106; для высокоглиноземистых с 72% Al203&=9,0-108).

По Вишневскому, для модели изометрических зерен, полностью окруженных прослойками расплава толщиной о> с вязкостью г^ж, ка­жущаяся вязкость тела г|Каж определяется формулой

%аж = ї|ж (d/w)2, (11.58)

Где d — размер зерен твердой фазы (см. формулу 11.37). .

Поскольку R=ATP для пластины, то можио записать для тела любой формы:

ДГкрип в S' + ■ *»<'-"> 5', (II.59)

Атікаж

Затем, используя понятие «период релаксации» (см. ниже), б — =тікаж/Е, где 9 —период релаксации; т]каж — кажущаяся вязкость; Е — модуль упругости; и, подставляя вместо тікаж его значение

Т|каж = ПОлуЧИМ

ДГкрип = Д(1 +1/9).

Из формулы (11.60) следует, что термостойкость изделий при вы­соких температурах определяется термостойкостью их при комнатной температуре и периодом релаксации материала.

Из формул (11.47 и 11.48) можно сделать вывод, что с увеличени­ем пористости термостойкость должна снижаться, так как при этом <7пч и Я уменьшаются быстрее, чем Е. Однако практикой это не под­тверждается. Теория «максимальных напряжений» указанного про­тиворечия не разрешает.

Теория «двух стадий»

По этой теории разрушение материалов под влиянием термиче­ских напряжений происходит в две стадии: зарождения трещин и их роста. Критерии термостойкости R, R[4] и Rn относятся к стадии за­рождения трещин.

Теория двух стадий не опровергает теорию максимальных напря­жений, а развивает ее. Зародившаяся трещина в гетерогенных ма­териалах, какими являются большинство огнеупоров, развивается медленно, а может и вообще не развиваться. По теории Гриффитса, трещины будут расти в том случае, если упругая энергия, освободив­шаяся из напряженной области, будет больше энергии, необходимой для создания двух новых поверхностей раздела.

По Хассельману, критерии распространения трещин выражаются следующими формулами:

(11.61) (11.62)

Где уЭф — эффективная энергия, необходимая для создания двух но­вых поверхностей раздела1.

Чтобы трещины не развивались, материал должен обладать вы­соким значением модуля упругости и низкой прочностью, а чтобы трещины не зарождались, модуль упругости должен быть низким, прочность высокой.

Кажущееся противоречие в самом деле не является противоре­чием. В гетерогенном материале трещины зарождаются в твердых фазах, и, чтобы трещины в них не зарождались, эти фазы должны иметь высокую прочность, а распространяются трещины во всем объ­еме многофазного материала: по твердым фазам и порам. Напряже­ния в порах гасятся. Для того чтобы трещины не развивались, мате­риал должен иметь поры, а следовательно, в целом быть менее проч­ным. В гомогенном материале (стекле) зародившаяся трещина растет без ограничения (катастрофическое разрушение), в гетерогенном же зародившиеся трещины обычно не приводят к немедленному разру­шению. Поэтому для оценки термостойкости гомогенных тел доста­
точными критериями будут R, R R11 и ДГР по Кингери, а также дГкряп. Для гетерогенных более важно распространение трещин, чем их зарождение, поэтому критериями термостойкости будут критерии по Хассельману и

Для понимания термостойкости гетерогенных тел большое зна­чение имеют работы Панарина. Известно, что хромит и магнезит (обожженный) по отдельности нетермостойки, а изделия, полученные из хромита и магнезита, имеют высокую термостойкость. Трещины, зарождающиеся при термоударах в магнезите и хромите, гасятся в порах определенного строения.

Критерий RIV удовлетворительно описывает термостойкость ог­неупоров микротрещиноватой текстуры и не подходит или не всегда подходит к оценке термостойкости зернистых материалов, хотя оба вида текстур относятся к гетерогенным.

Гогоци предложил классифицировать огнеупоры по их отноше­нию к термостойкости не по степени гетерогенности, а по мере хруп­кости. Термостойкость с учетом меры хрупкости выражается фор­мулой

Д*=Я(3 + Х)/43{. (И. 63)

Когда и=1, формула переходит в выражение (11.47). Для уче­та эластичности, возникающей при высоких температурах, мера хрупкости также должна быть определена при высоких темпера­турах.

Структурная (фрагментальная) теория термостойкости

Влияние пор на термостойкость определяется сложной ролью их в трансформации напряжений: экранизацией, концентрацией, глуше­нием напряжений при заходе трещины в пору (интеркристаллитные трещины) или выходом трещины из поры в кристалл (транскристал - литные трещины) и т. п. Если представить себе материал, состоящий из отдельных объемов (фрагментов), которые имели бы некоторую возможность перемещения относительно друг друга при термическом нагружении, то материал обладал бы высокой термостойкостью. Та­кой материал получают различными технологическими путями: при­меняют смеси компонентов шихт с различными термическими коэф­фициентами линейного расширения, смешивают огнеупорные глииы с различной спекаемостью (глииу и шамот), используют различный зерновой состав (крупные зерна спекаются хуже мелких и в резуль­тате этого между зернами получаются трещины, разделяющие объем материала на фрагменты), применяют направленные структуры, пред­ложенные Куколевым, и т. д. В общем установлено, что скорость Распространения трещин обратно пропорциональна исходной кон­центрации микротрещин. Теорией не определены оптимальные разме­ры фрагментов и концентрация микротрещин и др. Теория развива­ется. Перспективность ее очевидна, так как большинство термостой­ких огнеупороз магнезитохромитовых (МХС) и периклазошпинелид - НЬ1х (П1ІІС) созданы именно на качественных положениях этой теории. Отметим, однако, что создание фрагментальной текстуры не является универсальным способом повышения термостойкости. На­пример, динас с хорошим фрагментальным строением не обладает термостойкостью в широком диапазоне температур.

Статистическая теория термостойкости или теория «слабого звена»

Прочность, как известно, носнт статистический характер. Это! значит, что в отдельных участках напряжения могут быть больше среднего (слабое звено), а в других меньше. Поскольку термостой­кость зависит от прочности, то и термостойкость носит статистический характер. Для ее определения необходимо испытать несколько иден­тичных образцов (порядка 100) и вычислить статистические характе­ристики распределения термостойкости. Установлено, что значения термостойкости подчиняются закону нормального распределения. В результате статистической обработки полученных данных критерий термостойкости АГр вычисляют по формуле

ДГр = Ао0 Г (1 -)- 1 /т) S/Ea, (11.64)

Где А и S зависят от объема образца и распределения в нем темпера­туры; т — коэффициент гомогенности распределения по Вейбуллу (11.26); Г(1 + 1/т) —гамма-функция.

Термостойкость при напряжениях II рода

Напряжения II рода так же, как и I рода, могут быть больше* прочности материала. Например, химическое напряжение в магнези- тохромитовых изделиях при эксплуатации в мартеновских печах, по некоторым данным, в 60—100 раз превосходит напряжения I рода.

При создании композиционных материалов из веществ с различ­ными значениями а и Е необходимым условием получения высокой термостойкости материалов является соблюдение неравенств, выте­кающих из соотношения: Я^і»£2а2, а именно аі>аг при Еу<Е2 и а1<аг при Е{~^>Е2, где индексы 1 и 2 относятся к первой и второй фазам.

Определение термостойкости

Термостойкость огнеупоров определяют двумя методами. По пер­вому методу проводят одностороннее нагреваиие целого изделия при температуре горячего конца 1300° С и холодного конца при комнат­ной температуре и затем резко охлаждают изделие в проточной воде, погружая его в воду на 50 мм. Термостойкость выражают числом теплосмен до потери изделием в массе 20% —ТСіїоо. Этот метод яв­ляется стандартным.

По другому методу приготавливают кольцо, которое нагревают изнутри. Термостойкость выражают перепадом температур, при ко­тором кольцо разрушится — ДТр.

Для материалов, у которых лимитирующей стадией термического разрушения является распространение трещин, рекомендуется термо­стойкость выражать в теплосменах ТС^оо (%<1) и для гомогенных материалов (%«1) —по ДТ.